If vectors →P,→Q and →R have magnitude 5,12 and 13 units and →P+→Q=→R, the angle between →Q and →R is :
cos−1(512)
cos−1(513)
cos−1(1213)
cos−1(213)
The correct Answer is:3
→P+→Q=→RandP2+Q2=R2
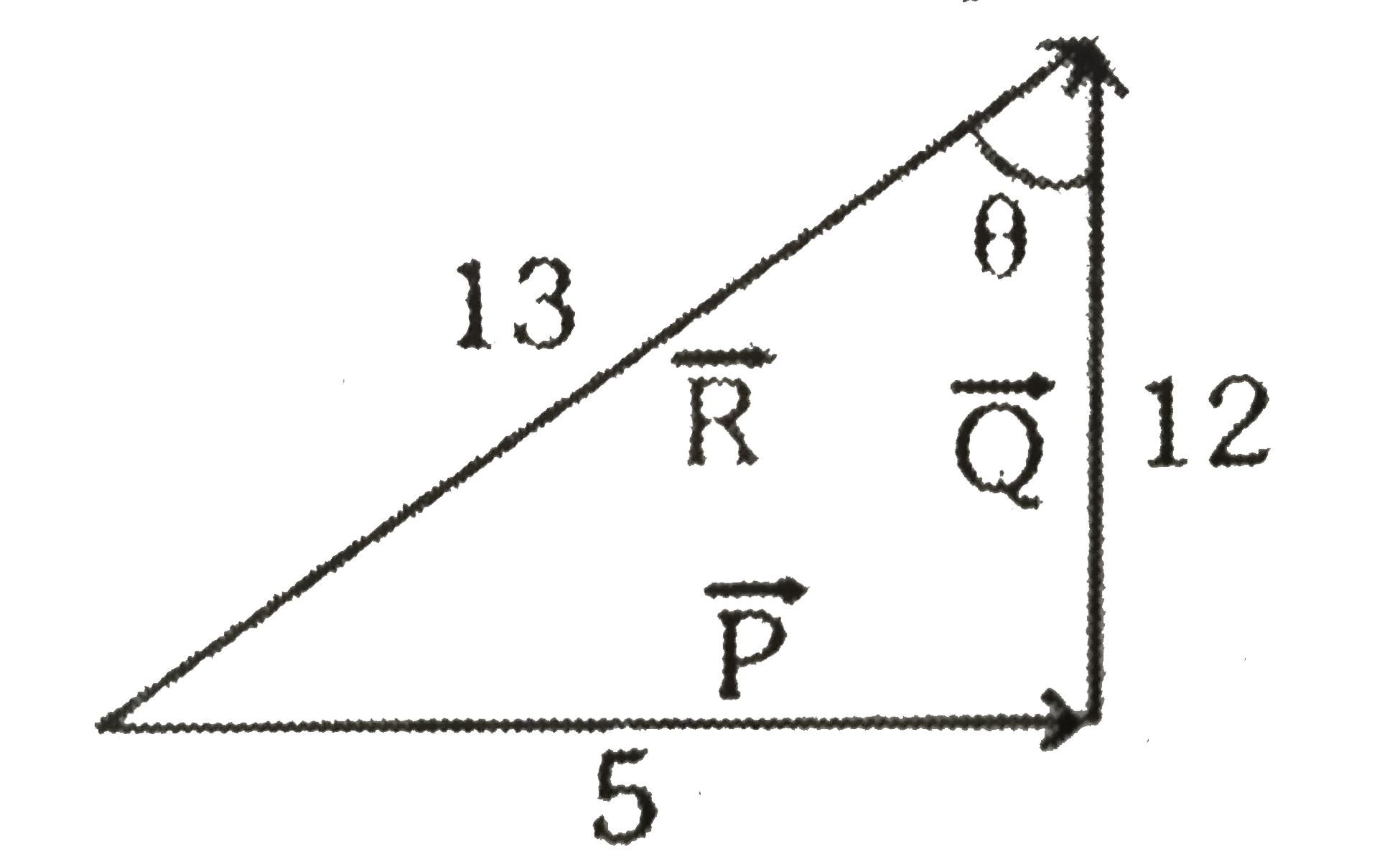
cosθ=1213⇒θ=cos−1(1213)
Topper's Solved these Questions
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - CROSS PRODUCT
15 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-II AIPMT/NEET & AIIMS (2006- 2018)
6 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - RESOLUTION OF VECTOR
8 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
Similar Questions
If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
View SolutionIf →P.→Q=PQ then angle between →P and →Q is
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣ the angle between →Pand→Q is
View Solutionif →P+→Q=→P−→Q, then
View Solution→P,→Q,→R,→S are vector of equal magnitude. If →P+→Q−→R=0 angle between →P and →Q is θ1 . If →P+→Q−→S=0 angle between →P and →S is θ2 . The ratio of θ1 to θ2 is
View Solutionif ∣∣→P+→Q∣∣=∣∣→P∣∣+∣∣→Q∣∣ , the angle between the vectors →Pand→Q is
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P∣∣−∣∣→Q∣∣ , the angle between the vectors →Pand→Q is
View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R. The distance between the points P and S is b∣∣→R∣∣. The general relation among vectors→P,→Q and →S is:
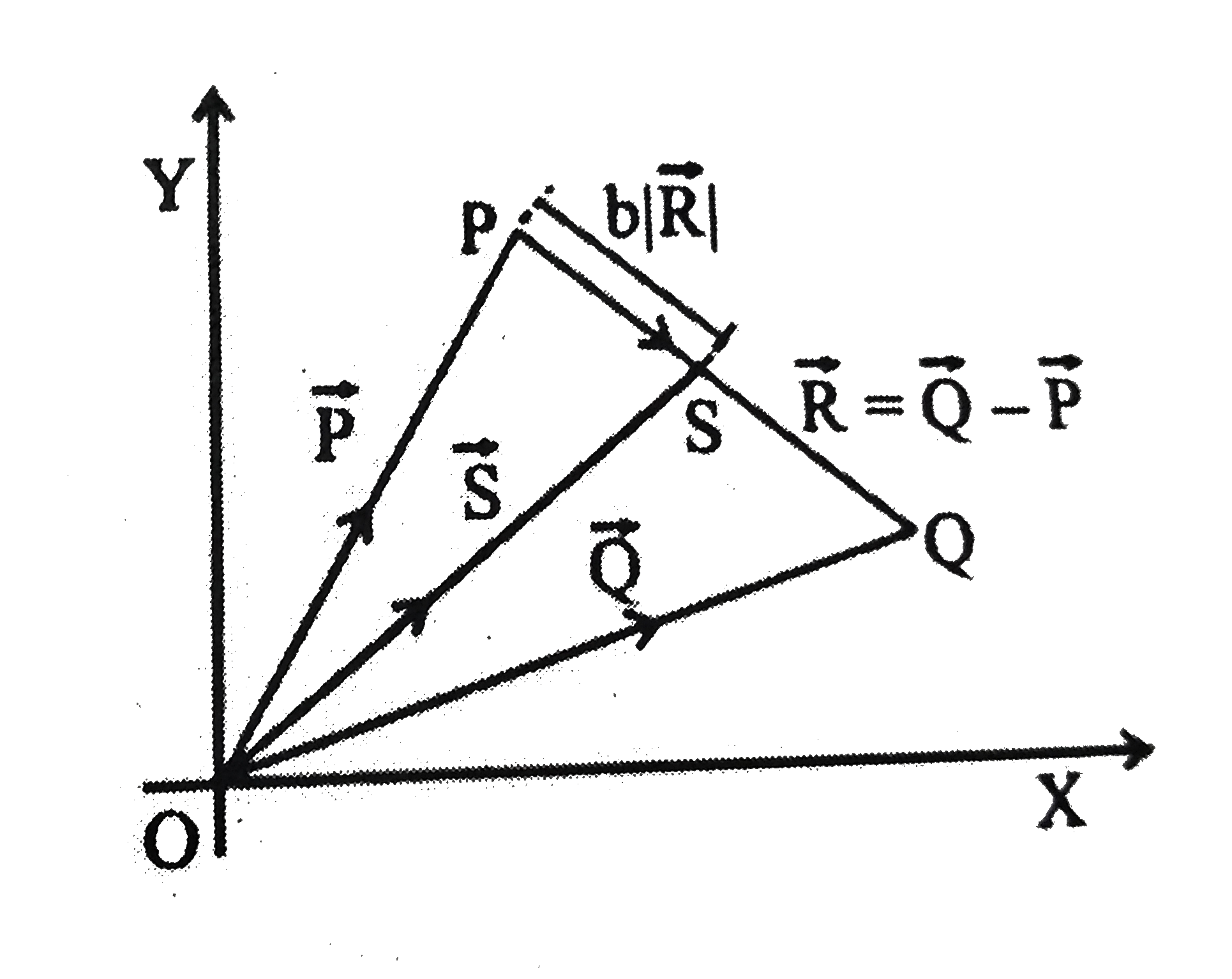
View SolutionMagnitude of resultant of two vectors →P and →Q is equal to magnitude of →P . Find the angle between →Q and resultant of →2P and →Q .
View SolutionTwo vectors →P and →Q are having their magnitudes in the ratio √3:1.Further।→P+→Q।=।→P−→Q। then the angle between the vectors (→P+→Q) and (→P−→Q) is
View Solution
