If vectors →P,→Qand→R have magnitudes 5, 12 and 13 units and →P+→Q=→R, the angle between →Qand→R is :
MLT−1C−1
MT2C−2
MT−1C−1
MT−2C−1
The correct Answer is:C
To solve the problem, we need to find the angle between the vectors →Q and →R given that →P+→Q=→R and their magnitudes are as follows:
- Magnitude of →P=5 units
- Magnitude of →Q=12 units
- Magnitude of →R=13 units
1. Express →P in terms of →Q and →R:
→P=→R−→Q
2. Use the magnitude relation:
We take the magnitude of both sides:
|→P|=|→R−→Q|
This gives us:
5=|→R−→Q|
3. Apply the formula for the magnitude of the difference of two vectors:
The magnitude of the difference of two vectors can be expressed as:
|→R−→Q|=√|→R|2+|→Q|2−2|→R||→Q|cos(θ)
where θ is the angle between →R and →Q.
4. Substitute the known magnitudes:
Substitute |→R|=13, |→Q|=12, and |→P|=5:
5=√132+122−2⋅13⋅12⋅cos(θ)
5. Square both sides:
25=169+144−2⋅13⋅12⋅cos(θ)
6. Simplify the equation:
25=313−312cos(θ)
Rearranging gives:
312cos(θ)=313−25
312cos(θ)=288
7. Solve for cos(θ):
cos(θ)=288312
Simplifying this fraction:
cos(θ)=1213
8. Find the angle θ:
θ=cos−1(1213)
Final Answer:
The angle between →Q and →R is θ=cos−1(1213).
- Magnitude of →Q=12 units
- Magnitude of →R=13 units
→P=→R−→Q
We take the magnitude of both sides:
|→P|=|→R−→Q|
This gives us:
5=|→R−→Q|
The magnitude of the difference of two vectors can be expressed as:
|→R−→Q|=√|→R|2+|→Q|2−2|→R||→Q|cos(θ)
where θ is the angle between →R and →Q.
Substitute |→R|=13, |→Q|=12, and |→P|=5:
5=√132+122−2⋅13⋅12⋅cos(θ)
25=169+144−2⋅13⋅12⋅cos(θ)
25=313−312cos(θ)
Rearranging gives:
312cos(θ)=313−25
312cos(θ)=288
cos(θ)=288312
Simplifying this fraction:
cos(θ)=1213
θ=cos−1(1213)
The angle between →Q and →R is θ=cos−1(1213).
Topper's Solved these Questions
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Exersice -05(B)
Explore 20 Videos
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Exercise-01
Explore 24 Videos
- BASIC MATHSBook:ALLENChapter:BASIC MATHSExercise:Exersice-4[B]
Explore 14 Videos
- AIIMS 2019Book:ALLENChapter:AIIMS 2019Exercise:PHYSICS
Explore 40 Videos
- CIRCULAR MOTIONBook:ALLENChapter:CIRCULAR MOTIONExercise:EXERCISE (J-A)
Explore 6 Videos
Similar Questions
If →P.→Q=PQ then angle between →P and →Q is
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P−→Q∣∣ the angle between →Pand→Q is
View Solutionif →P+→Q=→P−→Q, then
View Solutionif ∣∣→P+→Q∣∣=∣∣→P∣∣+∣∣→Q∣∣ , the angle between the vectors →Pand→Q is
View Solution→P,→Q,→R,→S are vector of equal magnitude. If →P+→Q−→R=0 angle between →P and →Q is θ1 . If →P+→Q−→S=0 angle between →P and →S is θ2 . The ratio of θ1 to θ2 is
View SolutionIf ∣∣→P+→Q∣∣=∣∣→P∣∣−∣∣→Q∣∣ , the angle between the vectors →Pand→Q is
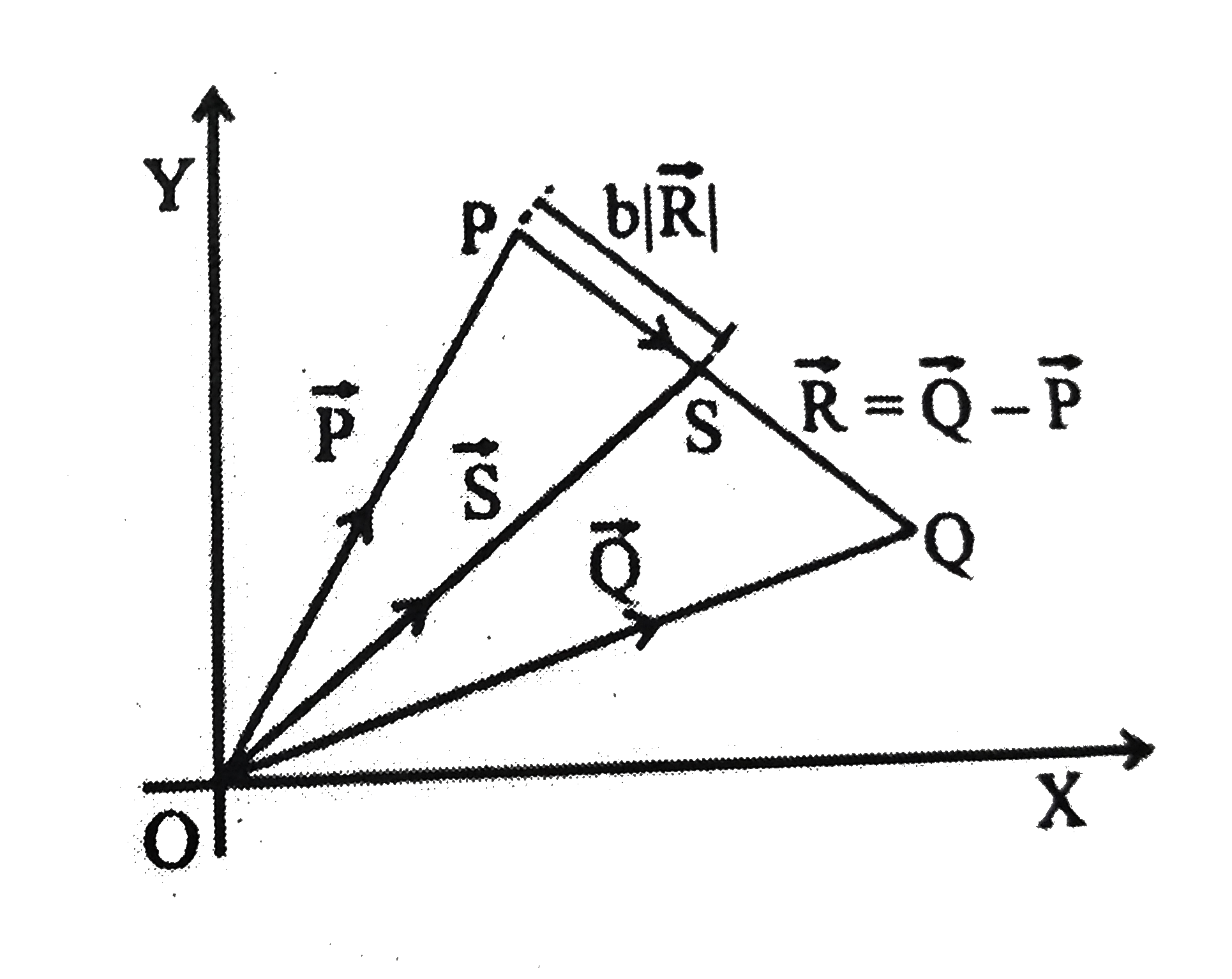
View SolutionThree vectors →P,→Q and →R are shown in the figure. Let S be any point on the vector →R. The distance between the points P and S is b∣∣→R∣∣. The general relation among vectors→P,→Q and →S is:
View SolutionTwo vectors →P and →Q are having their magnitudes in the ratio √3:1.Further।→P+→Q।=।→P−→Q। then the angle between the vectors (→P+→Q) and (→P−→Q) is
View SolutionThe resultant of →P and →Q is perpendicular to →P. What is the angle between →P and →Q
View SolutionMagnitude of resultant of two vectors →P and →Q is equal to magnitude of →P . Find the angle between →Q and resultant of →2P and →Q .
View Solution