A man when standstill observes the rain falling vertically and when he walks at 4km/h he has to hold his umberella at an angle 53∘ from the vertical. Find velocity of the raindrops.
To solve the problem, we need to analyze the situation using vector components and the concept of relative velocity. Here’s a step-by-step solution:
Step 1: Understand the Situation
When the man is standing still, he observes the rain falling vertically. This means that the velocity of the raindrops (V_rain) is directed straight downwards.
Step 2: Analyze the Man's Movement
When the man walks at a speed of 4 km/h, he has to hold his umbrella at an angle of 53 degrees from the vertical to keep himself dry. This indicates that the rain is not falling straight down relative to him; instead, it has a horizontal component due to his movement.
Step 3: Set Up the Velocity Vectors
1. Let the downward velocity of the rain be Vr (in km/h).
2. The horizontal velocity of the man is Vm=4 km/h (to the right).
3. The umbrella is held at an angle of 53 degrees from the vertical.
Step 4: Resolve the Velocity Components
When the man holds the umbrella at an angle of 53 degrees, we can resolve the velocities into their components:
- The vertical component of the resultant velocity (the effective velocity of the rain relative to the man) can be expressed as:
Vvertical=Vr
- The horizontal component (due to the man's walking) is:
Vhorizontal=Vm=4 km/h
Step 5: Use Trigonometry to Relate the Angles
Since the umbrella is at an angle of 53 degrees from the vertical, we can use the tangent function to relate the vertical and horizontal components:
tan(53∘)=VhorizontalVvertical
Substituting the known values:
tan(53∘)=4Vr
Step 6: Calculate Vr
We know that tan(53∘) is approximately 1.327 (or 43 in simplified form). Therefore, we can rearrange the equation:
Vr=4tan(53∘)
Substituting the value of tan(53∘):
Vr=41.327≈3 km/h
Final Answer
The velocity of the raindrops is approximately 3 km/h.
---
When the man is standing still, he observes the rain falling vertically. This means that the velocity of the raindrops (V_rain) is directed straight downwards.
When the man walks at a speed of 4 km/h, he has to hold his umbrella at an angle of 53 degrees from the vertical to keep himself dry. This indicates that the rain is not falling straight down relative to him; instead, it has a horizontal component due to his movement.
1. Let the downward velocity of the rain be Vr (in km/h).
2. The horizontal velocity of the man is Vm=4 km/h (to the right).
3. The umbrella is held at an angle of 53 degrees from the vertical.
When the man holds the umbrella at an angle of 53 degrees, we can resolve the velocities into their components:
- The vertical component of the resultant velocity (the effective velocity of the rain relative to the man) can be expressed as:
Vvertical=Vr
- The horizontal component (due to the man's walking) is:
Vhorizontal=Vm=4 km/h
Since the umbrella is at an angle of 53 degrees from the vertical, we can use the tangent function to relate the vertical and horizontal components:
tan(53∘)=VhorizontalVvertical
Substituting the known values:
tan(53∘)=4Vr
We know that tan(53∘) is approximately 1.327 (or 43 in simplified form). Therefore, we can rearrange the equation:
Vr=4tan(53∘)
Substituting the value of tan(53∘):
Vr=41.327≈3 km/h
The velocity of the raindrops is approximately 3 km/h.
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-1)
30 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
15 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
By the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.
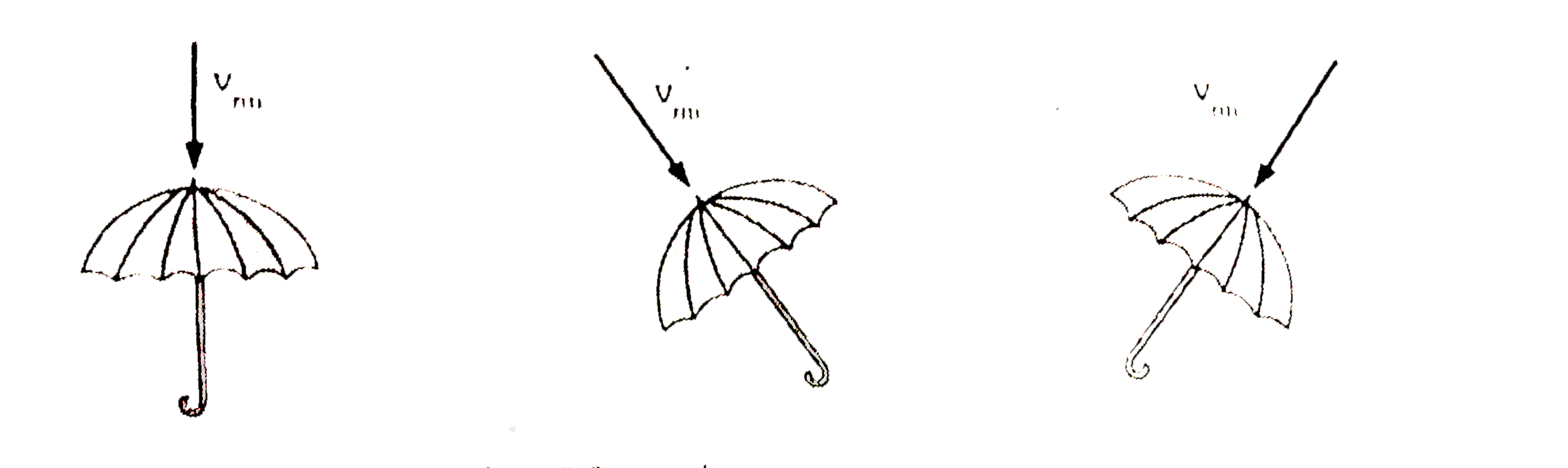
A man walks in rain at 72 cm/m due east and observes the rain falling vertically. When he stops, rain appears to strike his back at 37∘ from the vertical. Find velocity of raindrops relative to the ground.
View SolutionA person walking ,on a horizontal road at 2 km/h finds that the rain is falling vertically . Now the person increasses his speed to 4 km/h and find that rain makes an angle 45∘ with the vertical . Find the velocity of rain with respect to the road.
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionTo a man walking at the rate of 3km/h the rain appear to fall vertically downwards. When he increases his speed 6km/h it appears to meet him at an angle of 45∘ with vertically. Find the speed of rain.
View SolutionA man walking with a speed of 3 km/h finds the rain drops falling vertically downwards. When the man increases his speed to 6km/h he find that the rain drops are falling making an angle of 30∘ with the vertical . Find the speed of the rain drops ( in km/h)
View SolutionA stationary man observes that the rain is falling vertically downwards. When he starts running a velocity of 12kmh−1, he observes that the rain is falling at an angle 60∘ with the vertical. The actual velocity of rain is
View SolutionA man running at a speed of 5 km/h finds that the rain is falling vertically. When the stops running, the finds that the rain is falling at an angle of 60∘ with the horizontal. The velocity of rain with respect to running man is
View SolutionBy the term velocity of rain, we mean velocity with which raindrops fall relative to the ground. In absence of wind, raindrops fall vertically and in presence of wind raindrops fall obliqucly. Moreover raindrops acquire a constant terminal velocity due air resistance very quickly as they fall toward the carth. A moving man relative to himself observes an altered velocity of raindrops. Which is known as velocity of rain relative to the man. It is given by the following equation.
→vrm=→vr−→vm
A standstill man relative to himself observes rain falling with velocity, which is equal to velocity of the raindrops relative to the ground. To protect himself a man should his umbrella against velocity of raindrops relative to himself as shown in the following figure.

When you are standstill in rain, you have to hold umbrella vertically to protect yourself.
(a) When you walk with velocity 90 cm/s, you have to hold your umbrella at 53∘ above the horizontal. What is velocity of the raindrops relative to the ground and relative to you ?
(b) If you walk with speed 160 cm/s, how should you hold your umbrella ?
View SolutionTo a man walking at the rate of 4 km/h the rain appears to fall vertically. When he increases his speed 8 km/h it appears to meet him at an angle of 45 with vertical. Find the angle made by the velocity of rain with the vertical and its value.
View Solution
