A stationary man observes that the rain is falling vertically downwards. When he starts running a velocity of , he observes that the rain is falling at an angle with the vertical. The actual velocity of rain is
The correct Answer is:C
To solve the problem, we need to analyze the situation using vector components and trigonometry.
Step 1: Understand the scenario
A stationary observer sees the rain falling vertically. When he starts running at a speed of 12 km/h, he observes the rain falling at an angle of 60° with the vertical.
Step 2: Define the velocities
- Let Vm be the velocity of the man = 12 km/h (to the right).
- Let Vr be the actual velocity of the rain (which we need to find).
- The observed velocity of the rain with respect to the man, Vmr, makes an angle of 60° with the vertical.
Step 3: Set up the relationship
From the problem, we know:
Vmr=Vm−Vr
This means the velocity of the rain as observed by the man is the vector difference between the man's velocity and the actual velocity of the rain.
Step 4: Break down the observed velocity into components
Since the rain is falling at an angle of 60° with the vertical, we can break it down into components:
- The vertical component of the observed velocity of rain is Vmrcos(60°).
- The horizontal component of the observed velocity of rain is Vmrsin(60°).
Step 5: Use trigonometric relationships
From the angle:
- cos(60°)=12
- sin(60°)=√32
Thus, we can express the components as:
- Vertical component: Vmr⋅12
- Horizontal component: Vmr⋅√32
Step 6: Relate the components to the man's velocity
Since the rain appears to fall at an angle of 60° with the vertical, we can equate the horizontal component of the observed velocity to the man's velocity:
Vm=Vmr⋅√32
Step 7: Substitute the known values
Substituting Vm=12 km/h:
12=Vmr⋅√32
Step 8: Solve for Vmr
Rearranging gives:
Vmr=12⋅2√3=24√3=8√3 km/h
Step 9: Find the actual velocity of the rain
Now, we can find the actual velocity of the rain using the vertical component:
Vr=Vmr⋅cos(60°)
Vr=8√3⋅12=4√3 km/h
Final Answer
The actual velocity of the rain is 4√3 km/h.
---
A stationary observer sees the rain falling vertically. When he starts running at a speed of 12 km/h, he observes the rain falling at an angle of 60° with the vertical.
- Let Vm be the velocity of the man = 12 km/h (to the right).
- Let Vr be the actual velocity of the rain (which we need to find).
- The observed velocity of the rain with respect to the man, Vmr, makes an angle of 60° with the vertical.
From the problem, we know:
Vmr=Vm−Vr
This means the velocity of the rain as observed by the man is the vector difference between the man's velocity and the actual velocity of the rain.
Since the rain is falling at an angle of 60° with the vertical, we can break it down into components:
- The vertical component of the observed velocity of rain is Vmrcos(60°).
- The horizontal component of the observed velocity of rain is Vmrsin(60°).
From the angle:
- cos(60°)=12
- sin(60°)=√32
- Vertical component: Vmr⋅12
- Horizontal component: Vmr⋅√32
Since the rain appears to fall at an angle of 60° with the vertical, we can equate the horizontal component of the observed velocity to the man's velocity:
Vm=Vmr⋅√32
Substituting Vm=12 km/h:
12=Vmr⋅√32
Rearranging gives:
Vmr=12⋅2√3=24√3=8√3 km/h
Now, we can find the actual velocity of the rain using the vertical component:
Vr=Vmr⋅cos(60°)
Vr=8√3⋅12=4√3 km/h
The actual velocity of the rain is 4√3 km/h.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (A) Taking it together75videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - (B) Meical entrance special format questions (Assertion and reason)19videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Check point 3.620videos
MOTION IN A PLANE
- BOOK - DC PANDEY ENGLISHCHAPTER - MOTIONEXERCISE - Medical entrances gallery19videos
MOTION
- BOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective10videos
PROJECTILE MOTION
Similar Questions
A man running at a speed of 5 km/h finds that the rain is falling vertically. When the stops running, the finds that the rain is falling at an angle of 60∘ with the horizontal. The velocity of rain with respect to running man is
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA man starts running along a straight road with uniform velocity observes that the rain is falling vertically downward. If he doubles his speed, he finds that the rain is coming at an angle θ to the vertical. The velocity of rain with respect to the ground is :
View SolutionA man walking with a speed of 3 km/h finds the rain drops falling vertically downwards. When the man increases his speed to 6km/h he find that the rain drops are falling making an angle of 30∘ with the vertical . Find the speed of the rain drops ( in km/h)
View SolutionThere are two incline planes AO and OB inclined at 45∘ and 60∘ respectively with the horizontal as shown in the figure. When a man moves on the inclined plane AO he is oberves that the rain drops are falling 45∘ with the vertical. When the man moves on the inclined plane OB, he observes that the raindrops are falling vertically downward with the horizontal. Then actual speed of rain is
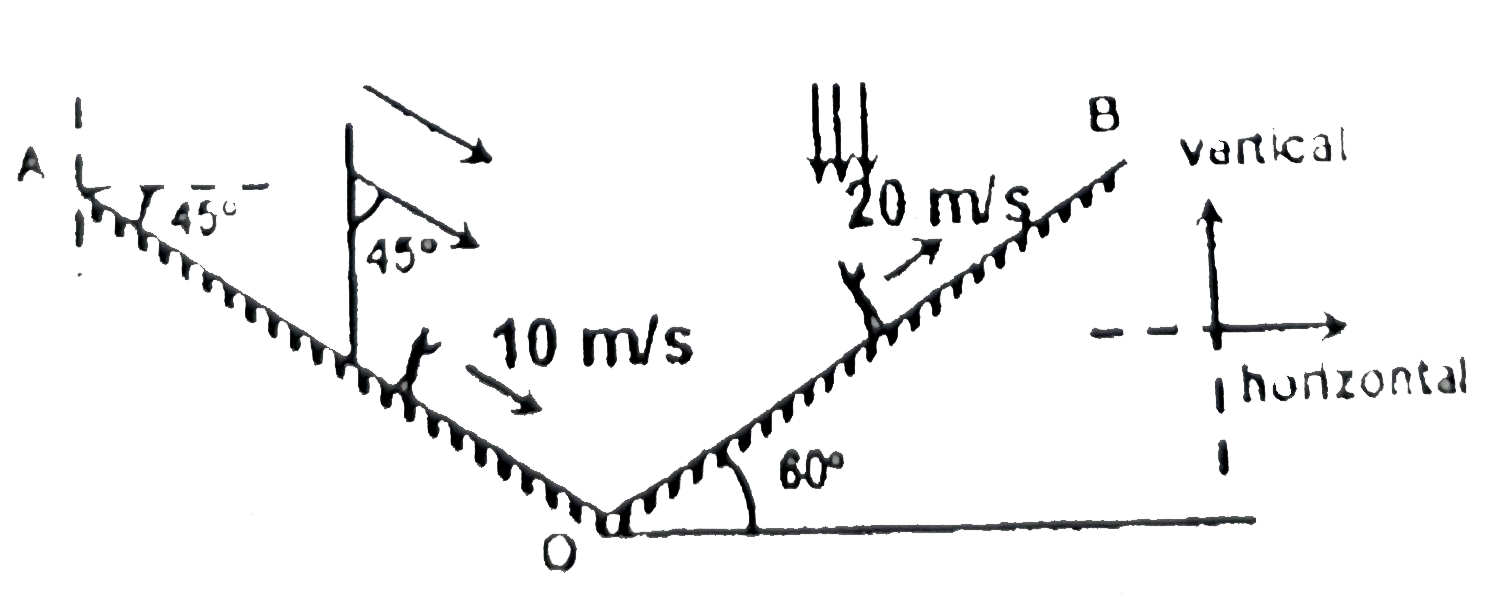 View Solution
View SolutionRain is falling vertically downwards with respect to ground. If a girl running on the ground with speed 3 km/h observes the rain is falling with speed 5 km/h then actual speed of rain is
View SolutionWhen a man moves down the inclined plane with a constant speed 5ms−1 which makes an angle of 37∘ with the horizontal, he finds that the rain is falling vertically downward. When he moves up the same inclined plane with the same speed, he finds that the rain makes an angle θ=tan−1(78) with the horizontal. The speed of the rain is
View SolutionA person walking ,on a horizontal road at 2 km/h finds that the rain is falling vertically . Now the person increasses his speed to 4 km/h and find that rain makes an angle 45∘ with the vertical . Find the velocity of rain with respect to the road.
View SolutionA man moves on a cycle with a velocity of 4 km/hr. The rain appears to fall on him with a velocity of 3 km/hr vertically. The actual velocity of the rain is
View SolutionA man standing on a inclined plain observes rain is falling verticaly. When he starts moving down the inclined plain with velocity v=6m/s observes rain hitting him horizontally.

The actual velocity of rain isView Solution
