Prithvi missile is fired to destroy an enemy military base situated on same horizontal level, situated 99 km away. The missile rises vertically for 1 km & then for remainder of flight, it followes parbolic path like a free body under earth's gravity, at an angle of 45∘. Calculate its velocity at beginning of parabolic path. (g=10ms−2)
To solve the problem of calculating the velocity of the Prithvi missile at the beginning of its parabolic path, we can break it down into several steps:
Step 1: Understand the problem
The missile rises vertically for 1 km and then follows a parabolic path at an angle of 45 degrees to cover a horizontal distance of 99 km. We need to find the initial velocity of the missile at the beginning of the parabolic path.
Step 2: Set up the coordinate system
Let's denote:
- The vertical displacement (rise) as sy=1km=1000m (upward).
- The horizontal displacement as sx=99km=99000m.
- The acceleration due to gravity as g=10m/s2.
Step 3: Resolve the velocity components
At the beginning of the parabolic path, the initial velocity u can be resolved into horizontal and vertical components:
- Horizontal component: ux=ucos(45∘)=u√2
- Vertical component: uy=usin(45∘)=u√2
Step 4: Calculate the time of flight in the horizontal direction
Using the horizontal motion equation:
sx=ux⋅t⟹99000=u√2⋅t
From this, we can express time t as:
t=99000√2u
Step 5: Apply kinematic equations in the vertical direction
Using the vertical motion equation:
sy=uy⋅t−12gt2
Substituting the known values:
1000=u√2⋅t−12⋅10⋅t2
Substituting t from the previous step:
1000=u√2⋅(99000√2u)−5(99000√2u)2
This simplifies to:
1000=99000−5⋅(99000)2⋅2u2
Step 6: Rearranging the equation
Rearranging gives:
5⋅(99000)2⋅2u2=99000−1000
5⋅(99000)2⋅2u2=98000
(99000)2⋅10u2=98000
u2=(99000)2⋅1098000
Step 7: Calculate u
Calculating u:
u2=(99000)2⋅1098000=9801000000⋅1098000=999000
u=√999000≈999.5m/s≈990m/s
Final Answer
The initial velocity of the missile at the beginning of the parabolic path is approximately 990m/s.
---
The missile rises vertically for 1 km and then follows a parabolic path at an angle of 45 degrees to cover a horizontal distance of 99 km. We need to find the initial velocity of the missile at the beginning of the parabolic path.
Let's denote:
- The vertical displacement (rise) as sy=1km=1000m (upward).
- The horizontal displacement as sx=99km=99000m.
- The acceleration due to gravity as g=10m/s2.
At the beginning of the parabolic path, the initial velocity u can be resolved into horizontal and vertical components:
- Horizontal component: ux=ucos(45∘)=u√2
- Vertical component: uy=usin(45∘)=u√2
Using the horizontal motion equation:
sx=ux⋅t⟹99000=u√2⋅t
From this, we can express time t as:
t=99000√2u
Using the vertical motion equation:
sy=uy⋅t−12gt2
Substituting the known values:
1000=u√2⋅t−12⋅10⋅t2
Substituting t from the previous step:
1000=u√2⋅(99000√2u)−5(99000√2u)2
This simplifies to:
1000=99000−5⋅(99000)2⋅2u2
Rearranging gives:
5⋅(99000)2⋅2u2=99000−1000
5⋅(99000)2⋅2u2=98000
(99000)2⋅10u2=98000
u2=(99000)2⋅1098000
Calculating u:
u2=(99000)2⋅1098000=9801000000⋅1098000=999000
u=√999000≈999.5m/s≈990m/s
The initial velocity of the missile at the beginning of the parabolic path is approximately 990m/s.
Topper's Solved these Questions
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-1)
30 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (S-2)
15 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
Similar Questions
A cracker is thrown into air with a velocity of 10m/s at an angle of 45∘ with the vertical. When it is at a height of 0.5m from the ground, it explodes into a number of pieces which follow different parabolic paths. What is the velocity of centre of mass, when it is at a height of 1m from the ground? (g=10m/s2)
View SolutionA body of mass 1kg is projected with velocity 50ms−1 at an angle of 30∘ with the horizontal. At the highest point of its path a force 10 N starts acting on body for 5s vertically upward besids gravitational force, what is horizontal range of the body (Take, g=10ms−2)
View Solution
Knowledge Check
Fire in Space
On Earth, fire provides light, heat, and comfort. Its creation, by a process called combustion, requires a chemical reaction between a fuel source and oxygen. The shape that fire assumes on Earth is a result of gravitational influence and the movement of molecules. In the microgravity environment of space, 34 moreover––––––––––, combustion and the resulting fire behave in fundamentally different ways than they do on Earth—differences that have important implications for researchers.
A group of engineering students from the University of California at San Diego (UCSD), for example, 35 tried to find a method to make their biofuel combustion study––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– (fuels derived from once-living material) free of the drawbacks researchers face on Earth. The standard method involves burning droplets of fuel, but Earth’s gravitational influence causes the droplets to lose spherical symmetry while burning. This 36 deformation––––––––––––– results in subtle variations in density that both 37 causes uneven heat flow and limits––––––––––––––––––––––––––––––––––––– the size of the droplets that can be tested. Specially designed “drop towers” 38 built for this purpose––––––––––––––––––––––– reduce these problems, but they provide no more than 10 seconds of microgravity, and droplet size is still too small to produce accurate models of combustion rates. 39 The UCSD students understood that these limitations had to be surmounted–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––. As part of the program, researchers fly their experiments aboard aircraft that simulate the microgravity environment of space. The aircraft accomplish this feat by flying in parabolic paths instead of horizontal ones. On the plane’s ascent, passengers feel twice Earth’s gravitational pull, but for brief periods at the peak of the trajectory, 40 (“weightlessness” or microgravity similar to what is experienced in space)––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– , is achieved. These flights allowed the UCSD students to experience microgravity 41 . Specifically, they 42 investigated––––––––––––– the combustion of biofuel droplets in microgravity for twice as long as could be accomplished in drop towers and to perform tests with larger droplets. The larger, 43 spherically symmetric–––––––––––––––––––––––– droplets burned longer and gave the students more reliable data on combustion rates of biofuels because the droplets’ uniform shape reduced the variations in density that hinder tests performed in normal gravity. The students hope the new data will aid future research by improving theoretical models of biofuel combustion. Better combustion-rate models may even lead to the production of more fuel-efficient engines and improved 44 techniques, for fighting fires in space or at future outposts–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––– on the Moon and Mars.
At this point, the writer is considering adding the following.
and perform their experiment without traveling into space Should the writer make this addition here?AYes, because it elaborates on the advantage the students gained from the flights.BYes, because it reveals that the students did not actually go into space, a point that the previous paragraph does not address.CNo, because it shifts focus away from the students’ experiences while on the flights.DNo, because it restates what has already been said in the sentence
When a particle is projected at some angle with the horizontal, the path of the particle is parabolic. In the process the horizontal velocity remains constant but the magnitude of vertical velocity changes. At any instant during flight the acceleration of the particle remains g in vertically downward direction. During flight at any point the path of particle can be considered as a part of circle and radius of that circle is called the radius of curvature of the path
Consider that a particle is projected with velocity u=10m/s at an angle θ=60∘ with the horizontal and take value of g=10m/s2. Now answer the following questions.
The radius of curvature of path of particle at the instant when the velocity vector of the particle becomes perpendicular to initial velocity vector is
View SolutionWhen a particle is projected at some angle with the horizontal, the path of the particle is parabolic. In the process the horizontal velocity remains constant but the magnitude of vertical velocity changes. At any instant during flight the acceleration of the particle remains g in vertically downward direction. During flight at any point the path of particle can be considered as a part of circle and radius of that circle is called the radius of curvature of the path
Consider that a particle is projected with velocity u=10m/s at an angle θ=60∘ with the horizontal and take value of g=10m/s2. Now answer the following questions.
The magnitude of acceleration of particle at that instant is
View SolutionWhen a particle is projected at some angle with the horizontal, the path of the particle is parabolic. In the process the horizontal velocity remains constant but the magnitude of vertical velocity changes. At any instant during flight the acceleration of the particle remains g in vertically downward direction. During flight at any point the path of particle can be considered as a part of circle and radius of that circle is called the radius of curvature of the path
Consider that a particle is projected with velocity u=10m/s at an angle θ=60∘ with the horizontal and take value of g=10m/s2. Now answer the following questions.
Tangential acceleration of particle at that instant is
View Solutiona projectile is fired from the surface of the earth with a velocity of 5ms−1 and angle θ with the horizontal. Another projectile fired from another planet with a velocity of 3ms−1 at the same angle follows a trajectory which is identical with the trajectory of the projectile fired from the earth.The value of the acceleration due to gravity on the planet is in ms−2 is given (g=9.8ms−2)
View SolutionA wedge of mass M=2m rests on a smooth horizontal plane. A small block of mass m rests over it at left end A as shown in figure. A sharp impulse is applied on the block, due to which it starts moving to the right with velocity v0=6ms−1. At highest point of its trajectory, the block collides with a particle of same mass m moving vertically downwards with velocity v=2ms−1 and gets stuck with it. If the combined body lands at the end point A of body of mass M, calculate length l. Neglect friction (g=10ms−2).

View SolutionA rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the plateform (g=10ms−2)
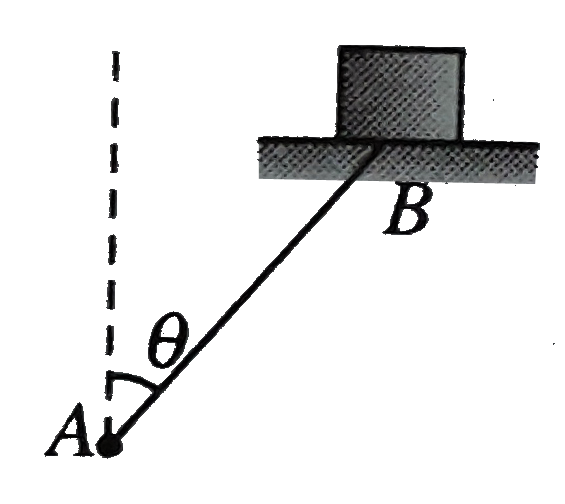
View SolutionA rod AB of length 2m is hinging at point A and its other end B is atteched to a platform on which a point of mass m is kept. Rod rotates about point A maintaing angle θ=30∘ with the vertical in such a way that platform remain horizontal and revolves on the horizontal circular path.If the coeffiicent of staic friction between the block and platform is μ=0.1 then find the maximum angular velocity in rads−1 of rod so that the block does not slip on the plateform (g=10ms−2)

View Solution
