The motion of a particle is described by the equation $x = a t + b t^{2}$ , where a = $15 c m s^{- 1}$ and b = $3 c m s^{- 2}$ . Its instantaneous velocity at t = 3 s will be

F is $\frac{v}{5}$

D is $\frac{v}{3}$

C is $\frac{v \sqrt{3}}{2}$

B is v

Video Solution

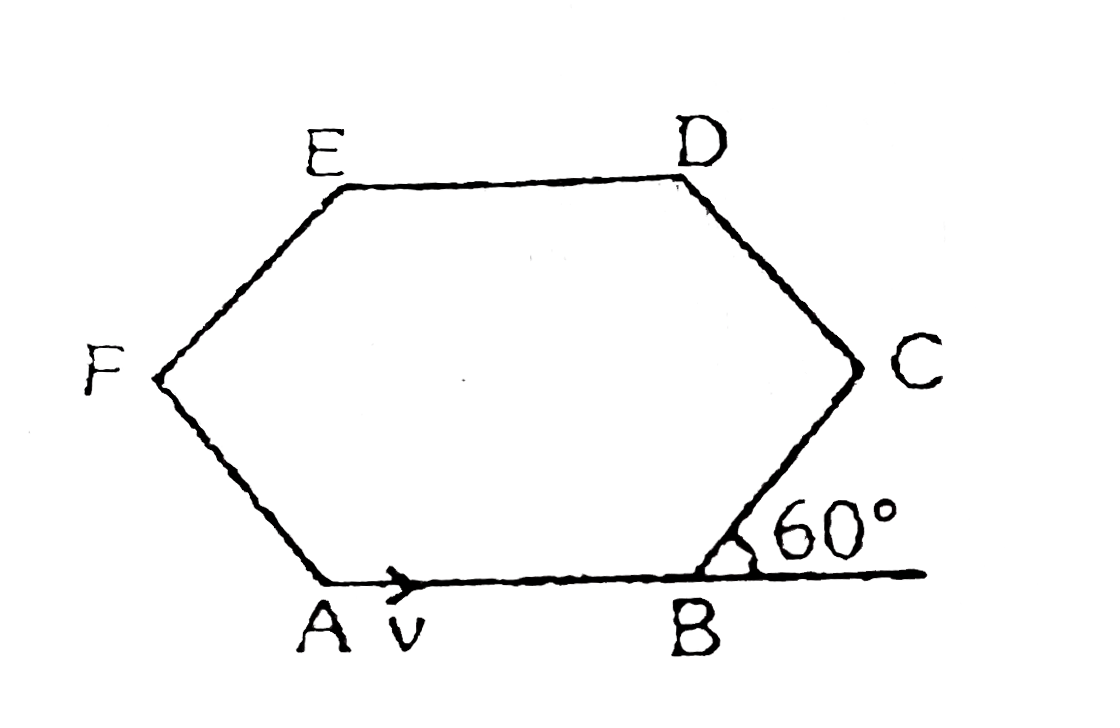
Text Solution

Verified by Experts

The correct Answer is:A, C, D

Updated on:21/07/2023

The motion of a particle is described by the equation $x = a + b t^{2}$ where $a = 15$ cm and $b = 3 c m / s^{2}$ . Its instantaneous velocity at time 3 sec will be
A $33 c m s^{- 1}$
B $18 c m s^{- 1}$
C $16 c m s^{- 1}$
D $32 c m s^{- 1}$
The position of an object moving along x-axis is given by $x = a + b t^{2}$ , where $a = 8.5 m$ and b=2.5 ms^(-2) and (t) is measured in seconds. What is the velocity at t=1= 0 $s and$ t=2.0 s? What is the average velocity between $t = 2.0 s$ and $t = 4.0 s$ ? a) 5 m/s b) 10 m/s c) 15 m/s d) 20 m/s
A $5 m s^{- 1}$
B $10 m s^{- 1}$
C $15 m s^{- 1}$
D $20 m s^{- 1}$