A force →F=6t2ˆi+4tˆj is acting on a particle of mass 3 kg then what will be velocity of particle at t=3 second and if at t=0, particle is at rest:-
If its speed changes, its velocity must change and it must have some acceleration
If its velocity changes, its speeds must change and it must have some acceleration
If its velocity changes, its speed may or may not change, and it must have some acceleration
If its speed changes but direction of motion does not change, its velocity may remain constant
The correct Answer is:A, C
To solve the problem, we need to find the velocity of a particle under the influence of a given force over a specific time interval. Let's break it down step by step.
Step 1: Identify the Given Information
We have:
- Force →F=6t2^i+4t^j
- Mass m=3kg
- Initial velocity →v(0)=0 (the particle is at rest)
- Time t=3s
Step 2: Use Newton's Second Law
According to Newton's second law, the force acting on an object is equal to the mass of the object multiplied by its acceleration:
→F=m→a
From this, we can express acceleration →a as:
→a=→Fm=6t2^i+4t^j3
This simplifies to:
→a=2t2^i+43t^j
Step 3: Relate Acceleration to Velocity
Acceleration is the rate of change of velocity:
→a=d→vdt
Thus, we can write:
d→v=→adt=(2t2^i+43t^j)dt
Step 4: Integrate to Find Velocity
To find the velocity, we integrate d→v:
→v=∫(2t2^i+43t^j)dt
This results in:
→v=(23t3^i+23t2^j)+→C
Since the particle is at rest at t=0, we can find the constant of integration →C:
→v(0)=0⟹→C=0
Thus, the velocity function simplifies to:
→v=23t3^i+23t2^j
Step 5: Evaluate Velocity at t=3s
Now, we substitute t=3 into the velocity equation:
→v(3)=23(33)^i+23(32)^j
Calculating each component:
→v(3)=23(27)^i+23(9)^j
→v(3)=18^i+6^j
Final Answer
The velocity of the particle at t=3s is:
→v(3)=18^i+6^j
---
We have:
- Force →F=6t2^i+4t^j
- Mass m=3kg
- Initial velocity →v(0)=0 (the particle is at rest)
- Time t=3s
According to Newton's second law, the force acting on an object is equal to the mass of the object multiplied by its acceleration:
→F=m→a
From this, we can express acceleration →a as:
→a=→Fm=6t2^i+4t^j3
This simplifies to:
→a=2t2^i+43t^j
Acceleration is the rate of change of velocity:
→a=d→vdt
Thus, we can write:
d→v=→adt=(2t2^i+43t^j)dt
To find the velocity, we integrate d→v:
→v=∫(2t2^i+43t^j)dt
This results in:
→v=(23t3^i+23t2^j)+→C
Since the particle is at rest at t=0, we can find the constant of integration →C:
→v(0)=0⟹→C=0
Thus, the velocity function simplifies to:
→v=23t3^i+23t2^j
Now, we substitute t=3 into the velocity equation:
→v(3)=23(33)^i+23(32)^j
Calculating each component:
→v(3)=23(27)^i+23(9)^j
→v(3)=18^i+6^j
The velocity of the particle at t=3s is:
→v(3)=18^i+6^j
Topper's Solved these Questions
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:EXERCISE-03
Explore 6 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:Assertion-Reason
Explore 20 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:SOLVED EXAMPLE
Explore 28 Videos
- KINEMATICS-2DBook:ALLENChapter:KINEMATICS-2DExercise:Exercise (O-2)
Explore 46 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
Similar Questions
Force acting on a particle of mass m moving in straight line varies with the velocity of the particle as F=K/V K is constant then speed of the particle in time t
View SolutionA time varying force, F=2t is acting on a particle of mass 2kg moving along x-axis. velocity of the particle is 4m/s along negative x-axis at time t=0. Find the velocity of the particle at the end of 4s.
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about the origin.
View SolutionStarting from rest, the acceleration of a particle is a=2(t-1). The velocity of the particle at t=5s is :-
View SolutionA force (ˆi−2ˆj+3ˆk) acts on a particle lying at origin. What is the torque acting on the particle about origin?
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
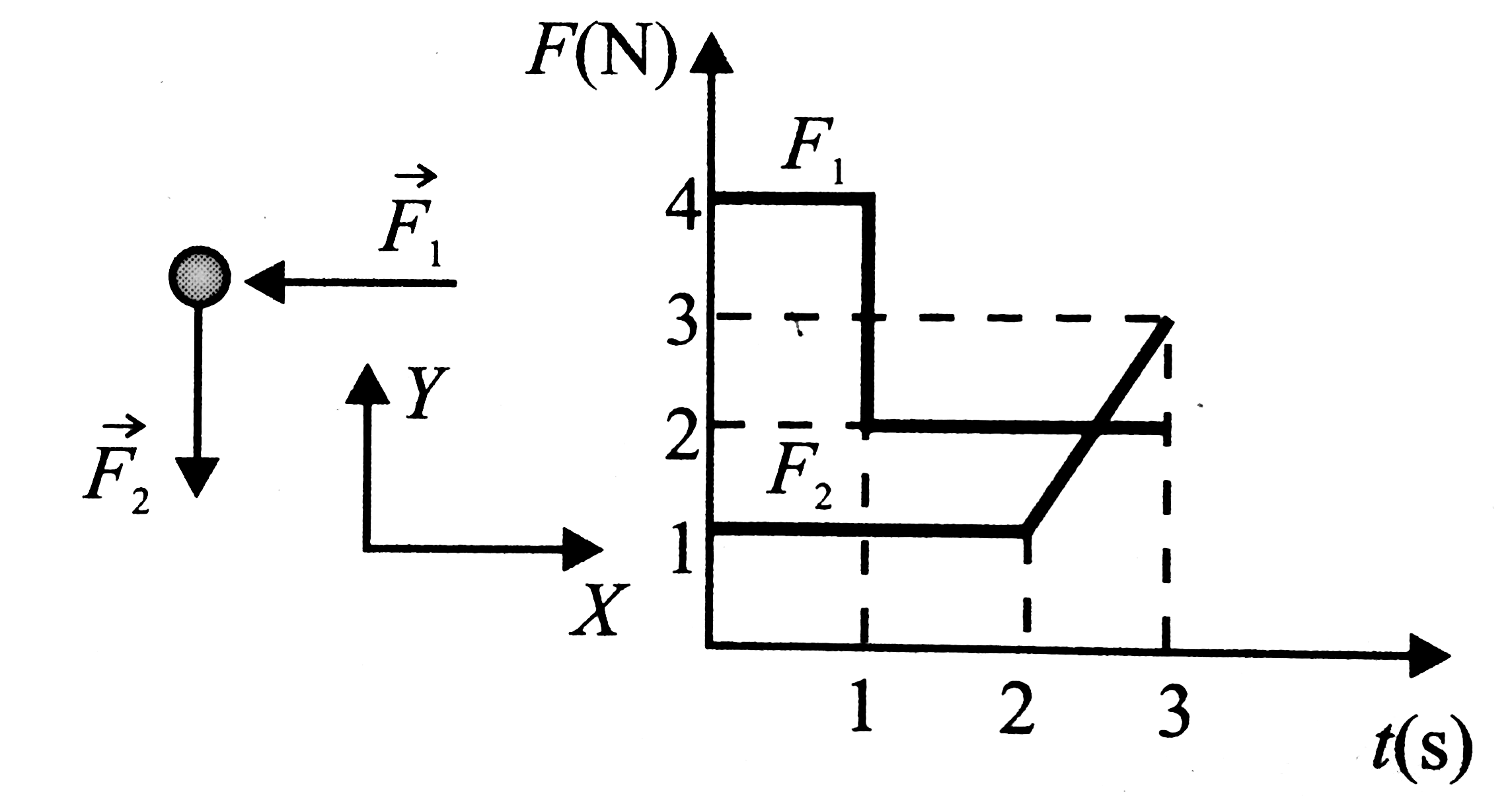
View SolutionA particle with a mass of 1kg a velocity of is having 10m/s in +vex-direction at t=0. Forces →F1 and →F2, act on the particle whose magnitudes are changing with time according to the variation shown in Fig. The magnitude of the velocity of the particle at t=3s (neglect gravity effect) is found to be n√5 Find the value of n
View SolutionIf acceleration a(t)=3t2 and initial velocity u=0 m/s , then the velocity of the particle after time t=4 s
View SolutionIn the figure the variation of components of acceleration of a particle of mass is 1kg is shown w.r.t. time. The initial velocity of the particle is →u=(−3i+4j)m/s. The total work done by the resultant force on the particle in time from t=0 to t=4 seconds is :
 .
.
View SolutionPosition time graph of a particle of mass 2 kg is shown in figrure. Total work done on the particle from t=0 to t=4s is

View Solution

