N(1)lambda(1) - N(2)lambda(2)

Consider radioactive decay of $A$ to $B$ with which further decays either to $X$ or $Y$ , $λ_{1}, λ_{2}$ and $λ_{3}$ are decay constant for $A$ to $B$ decay, $B$ to $X$ decay and Bto $Y$ decay respectively. At $t = 0$ , the number of nuclei of $A, B, X$ and $Y$ are $N_{0}, N_{0}$ zero and zero respectively.
$N_{1}, N_{2}, N_{3}$ and $N_{4}$ are the number of nuclei of $A, B, X$ and $Y$ at any instant $t$ .
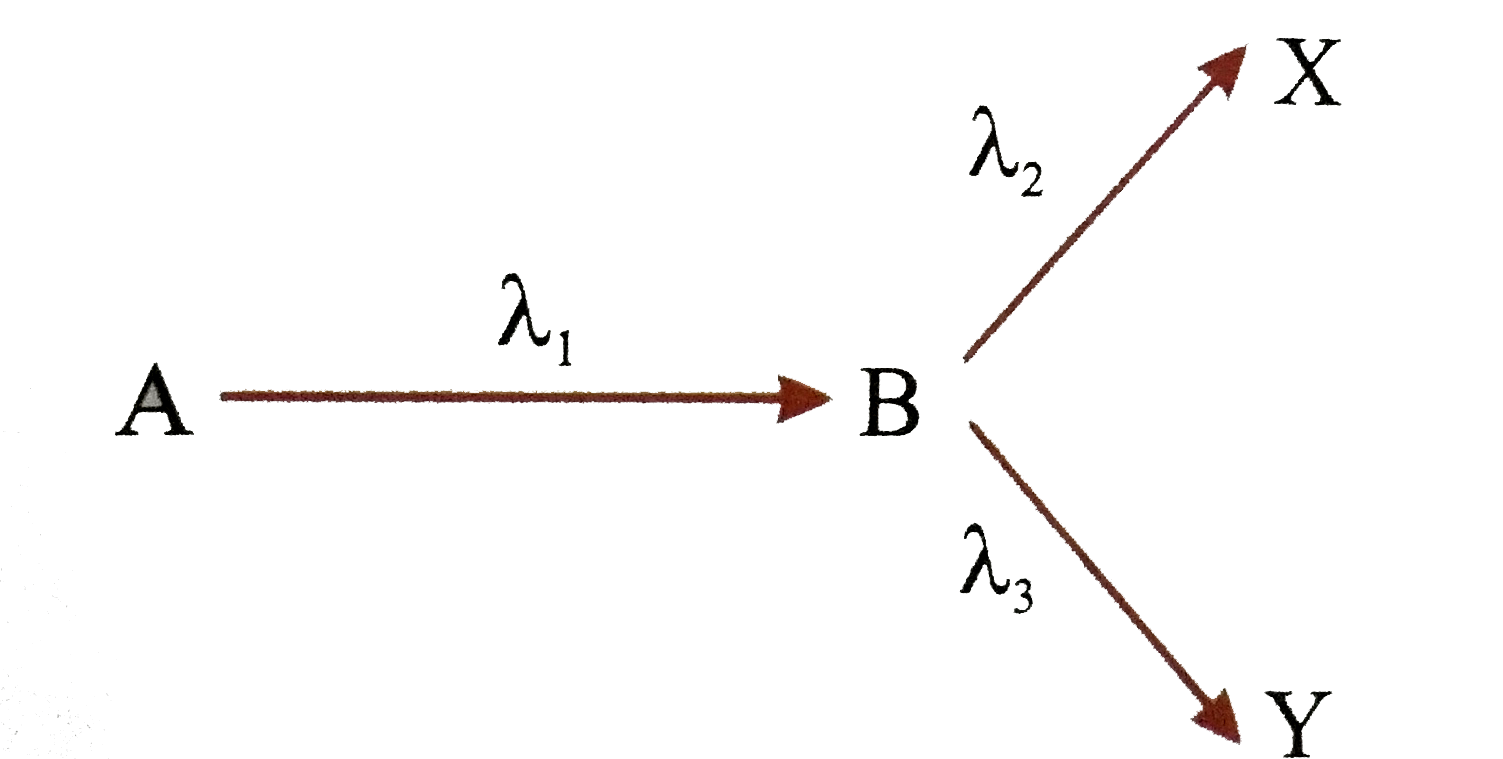
ocr_image
The number of nuclei of $B$ will first increase and then after a maximum value, it decreases for

View Solution

Replum is present in the ovary of flowers of

View Solution

The rate of biomass production by consumers is called $:$

View Solution

Two radioactive materials A & B have decay constant $3 λ$ and $2 λ$ respectively. At $t = 0$ the numbers of nuclei of A and B are $4 N_{0}$ and $2 N_{0}$ respectively then,

View Solution

Nucleus A decays into B with a decay constant $λ_{1}$ and B further decays into C with a decay constant $λ_{2}$ . Initially, at t = 0, the number of nuclei of A and B were $3 N_{0}$ and $N_{0}$ respectively. If at t = $t_{0}$ number of nuclei of B becomes constant and equal to $2 N_{0}$ , then

View Solution

Nucleus $A$ decays to $B$ with decay constant $λ_{1}$ and $B$ decays to $C$ with decay constant $λ_{2}$ . Initially at $t = 0$ number of nuclei of $A$ and $B$ are $2 N_{0}$ and $N_{0}$ respectively. At $t = t_{o}$ , no. of nuclei of $B$ is $\frac{3 N_{0}}{2}$ and nuclei of $B$ stop changing. Find $t_{0}$ ?

View Solution

In a decay process A decays to B. $A \to B$ . Two graphs of number of nuclei of A and B versus time is given then
ocr_image

View Solution

The decay constant $(λ)$ for radioactive decay is independent of

View Solution

A stable nuclei C is formed from two radioactive nuclei A and B with decay constant of $λ_{1}$ and $λ_{2}$ respectively. Initially, the number of nuclei of A is $N_{0}$ and that of B is zero. Nuclei B are produced at a constant rate of P. Find the number of the nuclei of C after time t.

View Solution

Consider a radioactive disintegration according to the equation $A \to B \to C$ . Decay constant of A and B is same and equal to $λ$ . Number of nuclei of A, B and C are $N_{0}$ , 0, 0 respectively at $t = 0$ . Find
(a) number of nuclei of B as function of time t.
(b) time t at which the activity of B is maximum and the value of maximum activity of B.

View Solution

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

ALLEN-SIMPLE HARMONIC MOTION-Exercise - 36

The correct Answer is:C

Rate of production of B depends on the decaying rate (A) : dNAdt=−λNA=λN1 B is decaying simultaneously with two rates dNBdt=−λ2NB=−λ2N2 dNBdt=−λ3NB=−λ3N2 Number of nuclei of 'B' is =λ1N1−λ2N2−λ3N2

Topper's Solved these Questions

Similar Questions

ALLEN-SIMPLE HARMONIC MOTION-Exercise - 36