A beaker contains water up to a height h1 and K oil above water up to another height h2. Find the apparent shift in the position of the bottom of the beaker when viewed from above. Refractive index of water is μ1 and that of K.oil is mu_2.
(1−1μ1)h2
(1−1μ1)h1+(1−1μ2)h2
(1−1μ1)h1
(1+1μ1)h2−(1+1μ2)h1
The correct Answer is:C
Apparent shift = h(1−1μ)
_E01_182_S01.png)
Total apparent shift = h1(1−1μ)+h2(1−1μ2)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-05 (B)
35 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - MCQ
5 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE-04[B]
18 Videos
- CURRENT ELECTRICITYBOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
A vessel contains water up to a height of 20 cm and above it an oil up to another 20 cm. The refractive indices of the water and the oil are 1.33 and F30 respectively. Find the apparent depth of the vessel when viewed from above.
View SolutionBottom of a glass beaker is made of a thin equi-convex lens having bottom side silver polished as shown in the figure. Water is filled in the beaker upto a height 4m. The image of poin to bject,floating at middle point of beaker at the surface of water coincides with it. Find out ther adius of curvature of the lens.Given that refractive index of glass is 3/2 and that of water is 4/3.

View SolutionA transparent solid sphere of radius 2cm and density ρ floats in a transparent liquid of density 2ρ kept in a beaker. The bottom of the beaker is spherical in shape with radius of curvature 8cm and is silvered to make it concave mirror as shown in the figure. When an object is placed at a distance of 10cm directly above the centre of the sphere C, its final image coincides with it. Find h (as shown in the figure ), the height of the liquid surface in the beaker from the apex of the bottom. Consider the paraxial rays only. The refractive index of the sphere is 3/2 and that of the liquid is 4/3.
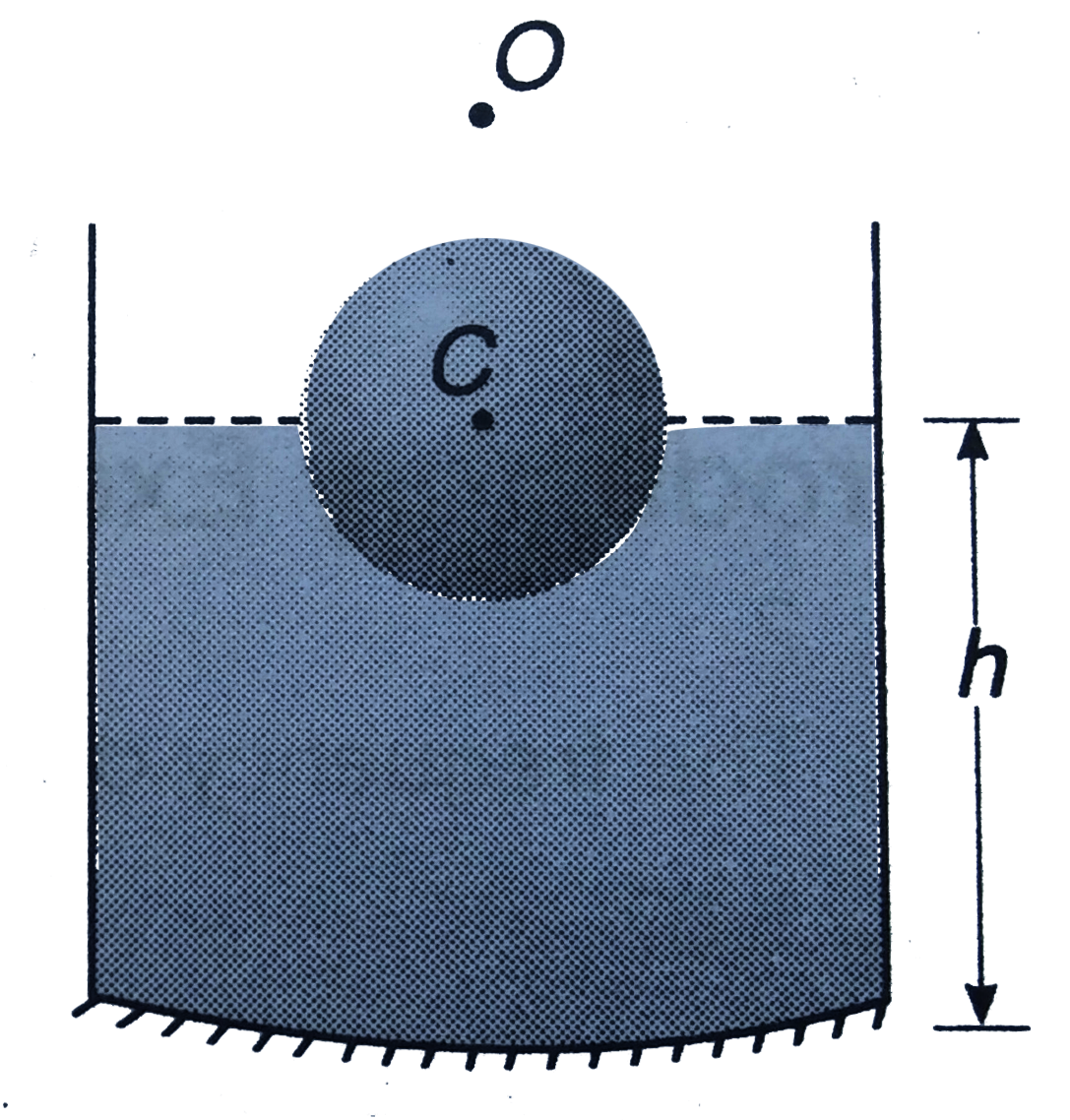
View SolutionA container contains water up to a height of 20 cm and there is a point source at the centre of the bottom of the container. A rubber ring of radius r floats centrally on the water. The ceiling of the room is 2.0 m above the water surface. (a) Find the radius of the shadow of the ring formed on the ceiling if r = 15 cm. (b) Find the maximum value of r for which the shadow of the ring is formed on the ceiling. Refractive index of water =4/3.
View SolutionHow much height of water in cm would be filled in a container of height 14 cm,so that it appears half filled to the observer when viewed from the top of the container (μω=43)
View SolutionHow much water should be filled in a container of height 21cm, so that it appears half filled to the observer when viewed from the top of the container (μ=4/3).
View SolutionHow much water should be filled in a container of height 21cm, so that it appears half filled to the observer when viewed from the top of the container (μ=4/3).
View SolutionIn a pond of water, a flame is held 2 m above the surface of the water. A fish is at depth of 4 m from the water surface. Refractive index of water is 43. The apparent height of the flame from the eyes of fish is -
View SolutionA coin at the bottom of a trough containing water to a depth of 15 cm appears to be 3.75 cm raised above from the bottom. Calculate the refractive index of water.
View SolutionImage of sun formed due to reflection at air water interface is found to be very highly polarised. Refractive index of water being μ=4/3, find the angle of sun above the horizon
View Solution
