Image of sun formed due to reflection at air water interface is found to be very highly polarised. Refractive index of water being μ=4/3, find the angle of sun above the horizon
37∘
53∘
30∘
60∘
To solve the problem, we need to find the angle of the sun above the horizon based on the information given about the polarization of light at the air-water interface. Here's the step-by-step solution:
Step 1: Understand the Concept of Polarization
The image of the sun is highly polarized due to reflection at the air-water interface. According to Brewster's Law, the angle at which light is perfectly polarized upon reflection is known as the polarizing angle (θp).
Step 2: Apply Brewster's Law
Brewster's Law states that:
μ=tan(θp)
where μ is the refractive index of the medium (water in this case), and θp is the polarizing angle.
Step 3: Substitute the Given Refractive Index
We are given that the refractive index of water (μ) is:
μ=43
Using Brewster's Law, we can find the polarizing angle:
θp=tan−1(43)
Step 4: Calculate the Polarizing Angle
Now we calculate θp:
θp=tan−1(43)≈53.1∘
Step 5: Find the Angle of the Sun Above the Horizon
The angle of the sun above the horizon (θ) can be determined using the relationship:
θ=90∘−θp
Substituting the value of θp:
θ=90∘−53.1∘≈36.9∘
Step 6: Round the Result
Rounding to the nearest whole number gives us:
θ≈37∘
Conclusion
Thus, the angle of the sun above the horizon is approximately 37 degrees.
Final Answer
The correct answer is 37 degrees.
---
The image of the sun is highly polarized due to reflection at the air-water interface. According to Brewster's Law, the angle at which light is perfectly polarized upon reflection is known as the polarizing angle (θp).
Brewster's Law states that:
μ=tan(θp)
where μ is the refractive index of the medium (water in this case), and θp is the polarizing angle.
We are given that the refractive index of water (μ) is:
μ=43
Using Brewster's Law, we can find the polarizing angle:
θp=tan−1(43)
Now we calculate θp:
θp=tan−1(43)≈53.1∘
The angle of the sun above the horizon (θ) can be determined using the relationship:
θ=90∘−θp
Substituting the value of θp:
θ=90∘−53.1∘≈36.9∘
Rounding to the nearest whole number gives us:
θ≈37∘
Thus, the angle of the sun above the horizon is approximately 37 degrees.
The correct answer is 37 degrees.
Similar Questions
A water pond appears to be 2⋅7m dep. If the refractive index of water is 4/3, find the actual depth of the pond.
View SolutionA pond appears to be 2.7 m deep. If the refractive index of water is 43, find the actual depth of the pond.
View SolutionBrewster angle for air to water transition is (refractive index of water is 43)
View SolutionA coin placed at the bottom of a beaker appears to be raised by 4.0 cm. If the refractive index of water is 4/3, find the depth of the water in the beaker.
View SolutionIf the speed of light in air is 3×108 m/s, and the refractive index of water is 1.33, find the speed of light in water.
View SolutionAt what angle to the horizon the sun be for is reflected rays from the surface of pond to be completely polarized (μ of water =1.33)
View SolutionAn object O is kept in air and a lens of focal length 10cm (in air) is kept at the botton of a container which is filled upto a height 44cm by water. The refractive index of water is 4/3 and that of glass is 3/2. The botton of the container is closed by a thin glass slab of refractive index 3/2. Find the distance (in cm) of the final image formed by the system from botton of container (refer to figure shown below).
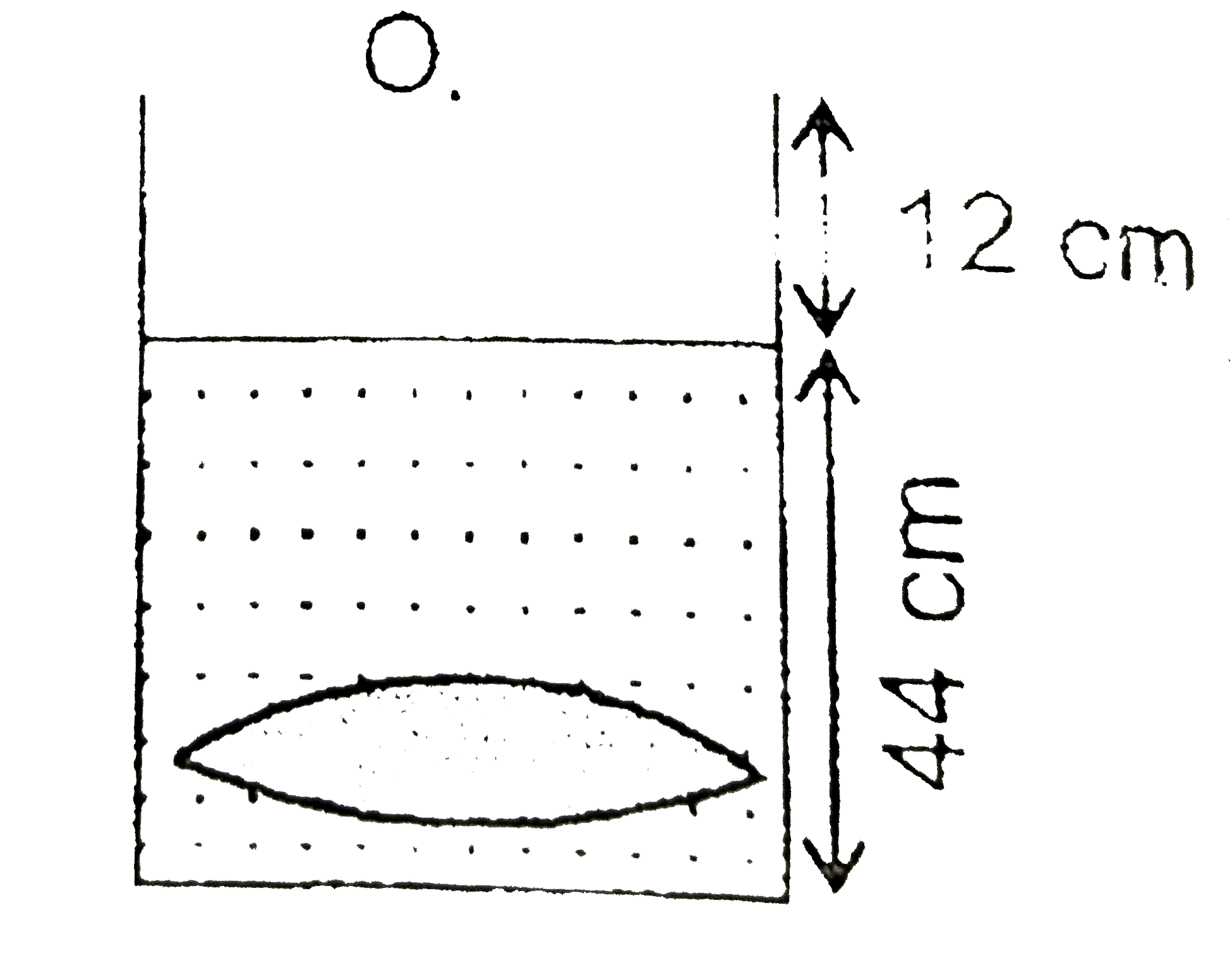
View SolutionA fish lies at the bottom of a 4m deep water lake. A bird flies 6m above the water surface and refractive index of water is 4/3 . Then the distance between
View SolutionAn insect at point 'P' sees its two images in the water mirror system as shown in the figure. One image is formed due to direct partical reflection from water surface and the other image is formed due to refraction, reflection & again refraction by water mirror system in order. Find the separation (in cm) between the two images. Mirror M has focal length 60 cm [Takeμw=4/3]
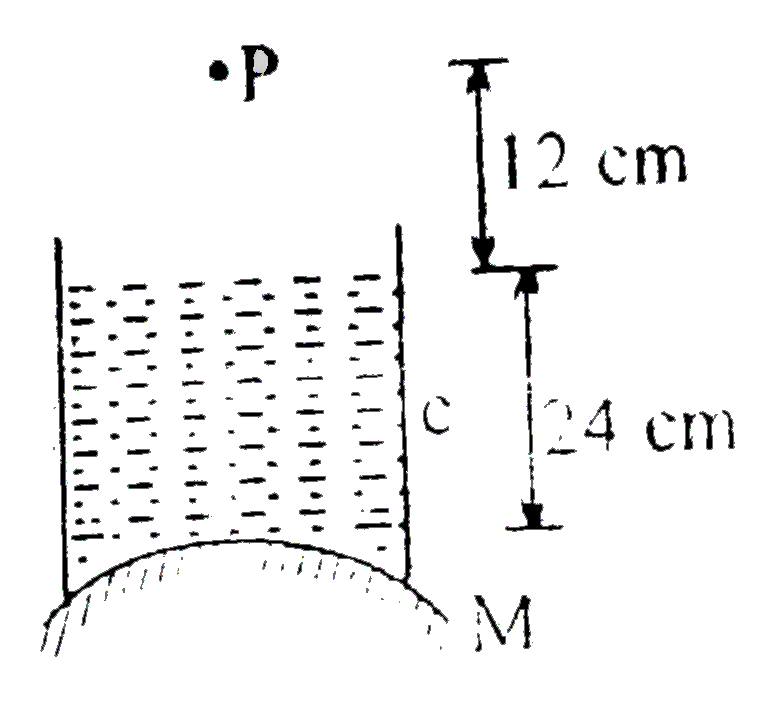
View SolutionA spherical mirror is placed 10 cm below the level of water. A point oject is placed in air 30 cm above the water surface on the axis of the mirror such that two images seen by an observer above the water surface coincide. The images are formed by partial reflection at the water surface and due to emerging light after feflection from the mirror. Find the focal length of the mirror. (μwater=43)
View Solution
