On one boundary of a swimming pool , there is a person at point A whose speed of running on group (boundary) is 10ms−1 , while that of swimming is 6ms−1 . He has to reach a point B in the swimming pool . The distance covered on the boundary so that the time required to reach the point B in the pool is minimum, is
_S01_048_Q01.png)
10m
6m
7m
√116m
The correct Answer is:C
_S01_048_S01.png)
Required time t=x10+(√42+(10−x)2)5 for minimum time dtdx=0⇒x=7m
OR
Just like light , he has different speeds on ground and in water , so to minimize the time, Fermat's principle must hold good.
SinθC=610=35⇒θC=37∘⇒tanθC=34=10−x4⇒x=7m
_S01_048_S02.png)
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0165videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -0282videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective14videos
GEOMETRICAL OPTICS
- BOOK - ALLENCHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II66videos
CURRENT ELECTRICITY
- BOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 49videos
GRAVITATION
Similar Questions
A man swims from a point A on the bank of a river if width 100m. When he swims perpendicular to the water current, he reaches the other bank 50m downstream. The angle to the bank at which he should swim, to reach the directly opposite point B on the other bank is.
.View SolutionPerson aiming to reach the exactly opposite point on the bank of a stream is swimming with a speed of 0.5ms−1 at an angle of 120∘ with the direction of flow of water.The speed of water in the stream is
View SolutionTwo swimmers start at the same time from point A one bank of a river to reach point B on the other bank, lying directly oppostie to point A. one of them crosses the river along the straight line AB, while the other swims at right angles to the stream and then walks the distance, which he has been carried awayby the stream to get to point B. Both swimmers reach point B at the same time. what was the velocity (assumed uniform) of his walking if velocity of both the swimmers in still water is 2.5 km h−1 and the stream velocity is 2 km h−1?
View SolutionA man can swim with speed 5ms−1 in still river while the river is also flowing speed 10ms−1 If the width of the river is 100 m then minimum possible drift is
View SolutionIn the figure shown a river of width 4m is flowing with speed of 5m/s. A swimmer whose swimming speed relative to the water is 4ms, starts swimming from a point A on a bank. On the other bank B is a point which is directly opposite to A. What minimum distance (in m) the swimmer will have to walk on the other bank to reach the point B.
View SolutionA body is moving along the +ve X-axis with uniform acceleration of −4ms2 Its velocity at x = 0 is 10ms−1. The time taken by the body to reach a point at x = 12m is
View SolutionTwo persons P and Q crosses the river starting from point A on one side to exactly opposite point B on the other bank of the river. The person P crosses the river in the shortest path. The person Q crosses the river in shortest time and walks back to point B. Velocity of river is 3 kmph and speed of each boat is 5 kmph w.r.t river. If the two persons reach the point B in the same time, then the speed of walk of Q is
View SolutionA sound wave of frequency 100 Hz is travelling in air. The speed of sound in air is 350ms−1 (a) By how much is the phase changed at a given point in 2.5 ms ? (b) What is the phase difference at a given instant between two points separated by a distance of 10.0 cm along the direction of propagation ?
View SolutionAn aeroplane has to go from a point O to another point A, at distance d due 37∘ East of North. A wind is blowing due North at a speed of 10ms−1. The air speed of the plane is v. (i) Find the direction in which the pilot should head the plane to reach the point A. (ii) Find the time taken by the plane to go from O to A.
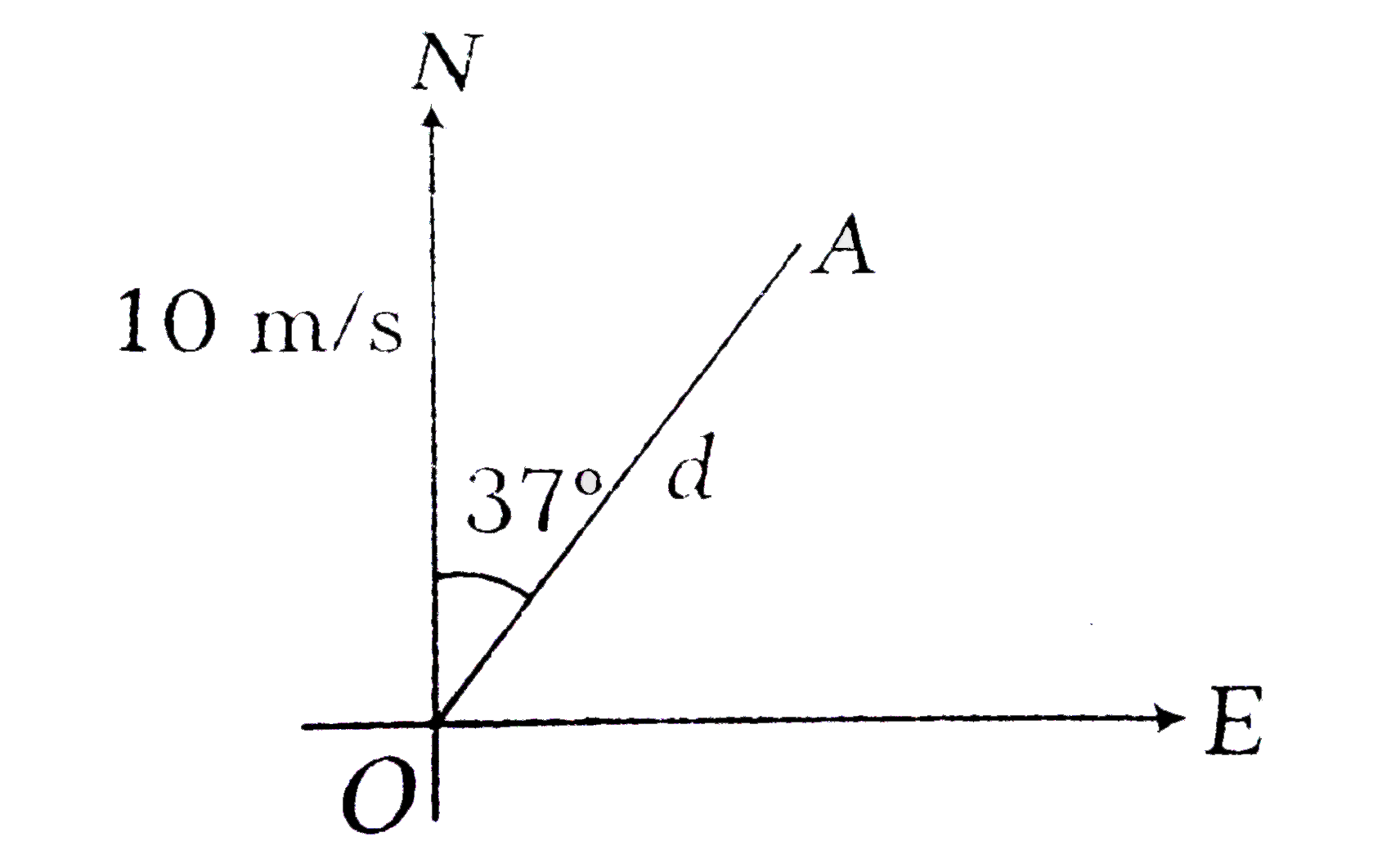View SolutionA man is walking towards a vertical pillar in a straight path at a uniform speed. At a certain point A on the path, he observes that the angle of elevationof the top of the pillar is 30∘. After walking for 5(√3+1) minutes from A in the same direction, at a point B, he observes that the angle of elevation of the top of the pillar is 45∘. Then the time taken (in minutes) by him, to reach from B to the pillar, is (take √3=1.73)
View Solution