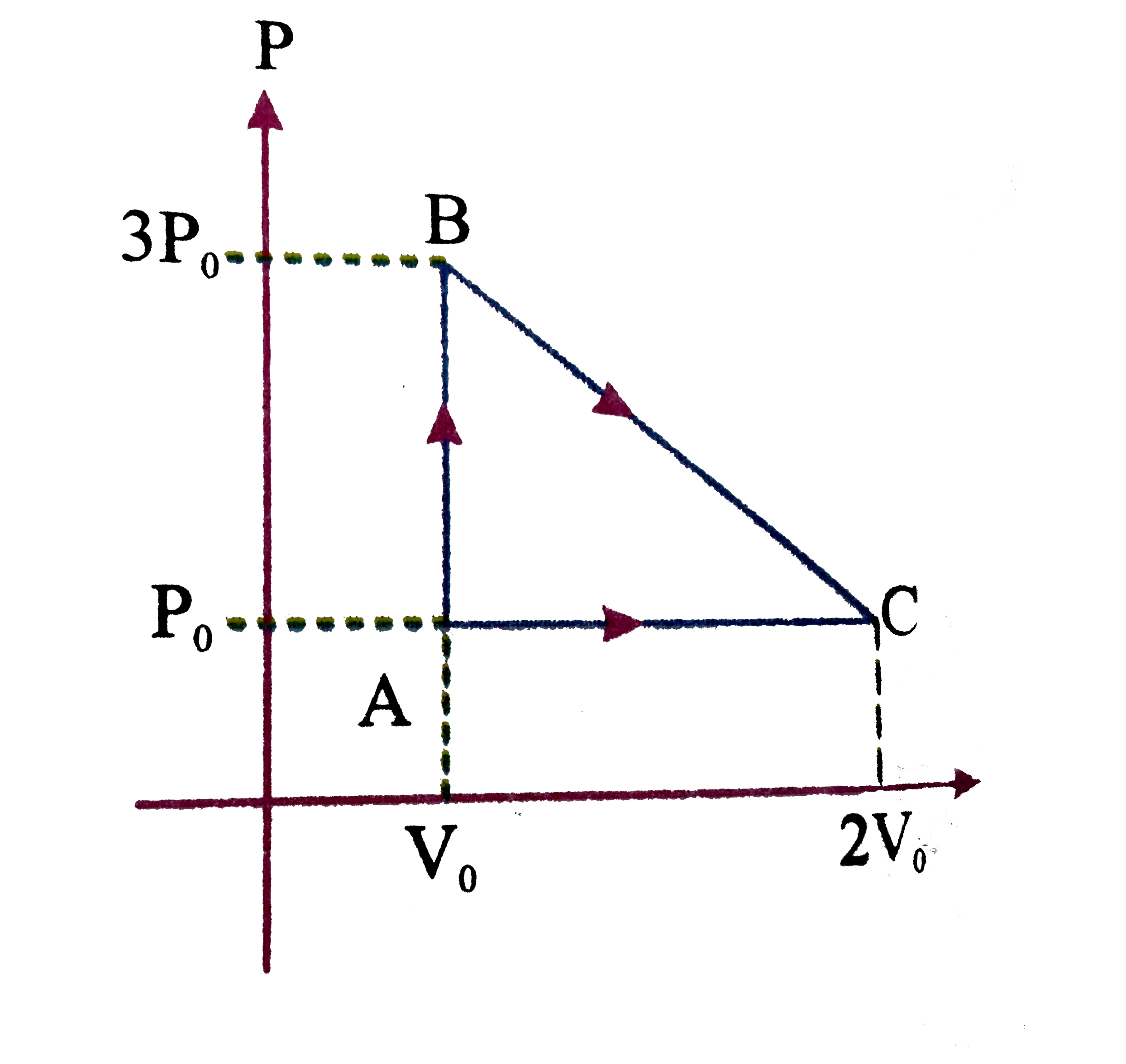
One mole of an ideal mono-atomic gas is taken round cyclic process as shown in figure below. Calculate work done by the gas.
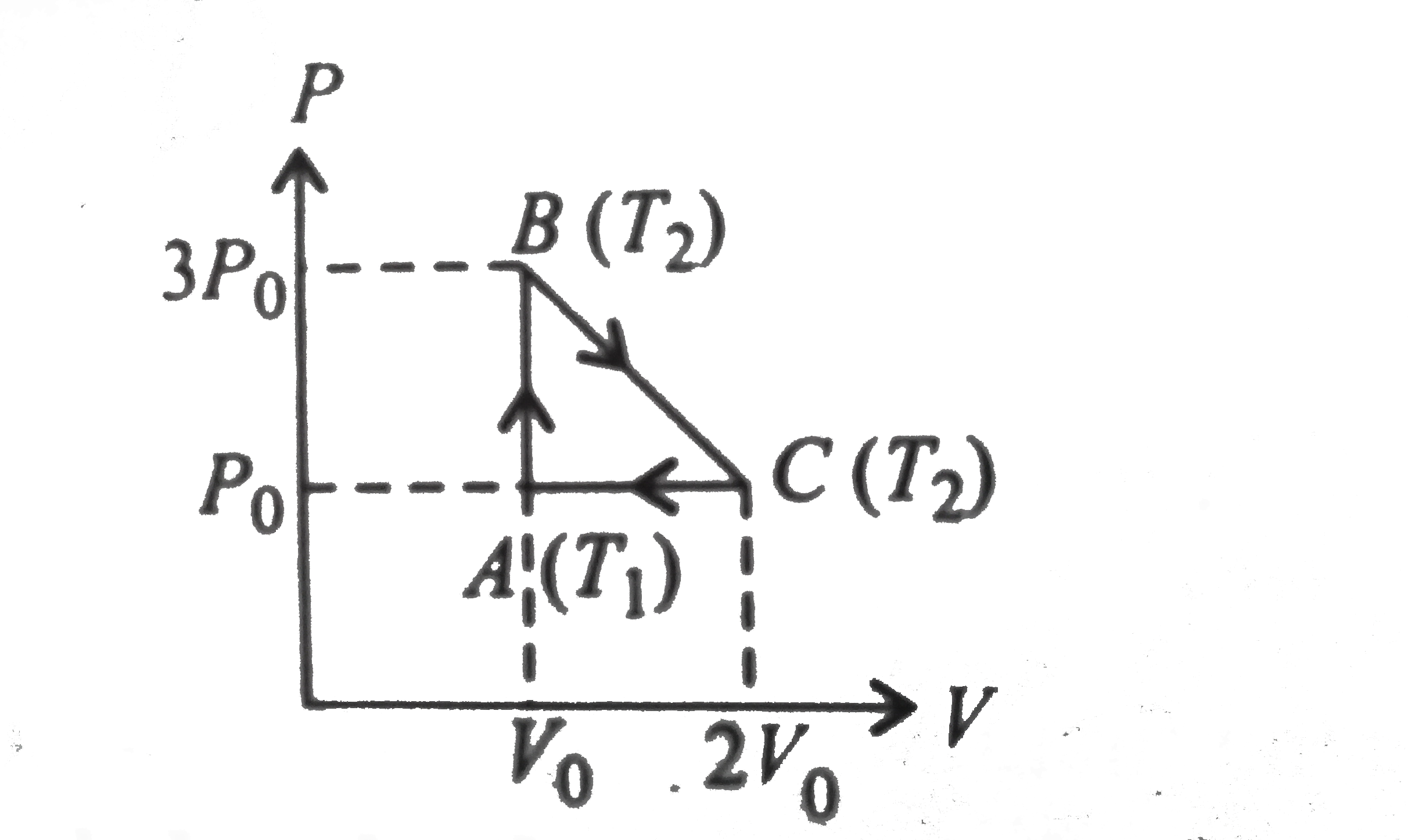
The correct Answer is:(i)
(a) is a clockwise cyclic process.
_E01_438_S01.png)
Work done by the gas
W = +Area pf triangle
(base)(height) =
(b) No. of moles and gas is monoatomic ,
(i) Heat rejected in path
Substituting the values
Therefore,heat rejected in the process
(ii) Heat absorbed in path :
=
=
Heat absorbed in the process
(c) Let be the heat absorbed in the process Total heat absorbed
Change in internal energy
Heat absorbed in the process is
(d) Maximum temperature of the gas will some where between B and C . Line is a straight line . Therefore , equation for the process BC can be written as
Here ,
Multiplying the equation by
For to be maximum
i.e., at (on line BC), temperature of the gas is maximum
From Equation (i) this maximum temperature will be
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 05 (B) (MCQ)
Explore 9 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 05 (B) (MATCH THE COLUMN)
Explore 3 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE - 05 (A)
Explore 73 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
One mole of an ideal mono-atomic gas is taken round cyclic process ABC as shown in figure below. Calculate work done
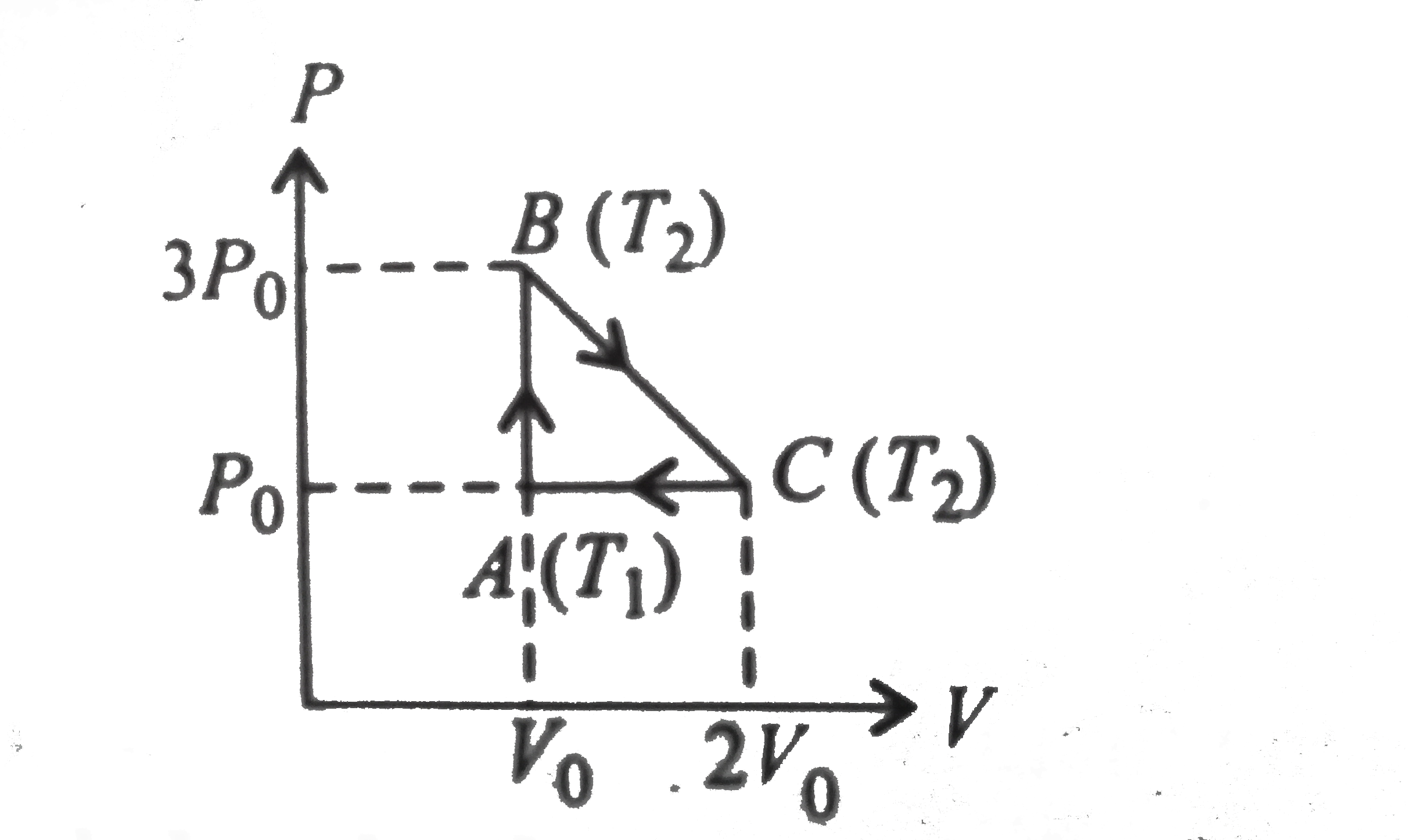
View SolutionOne mole of an ideal mono-atomic gas is taken round cyclic process ABC as shown in figure below. Calculate work done
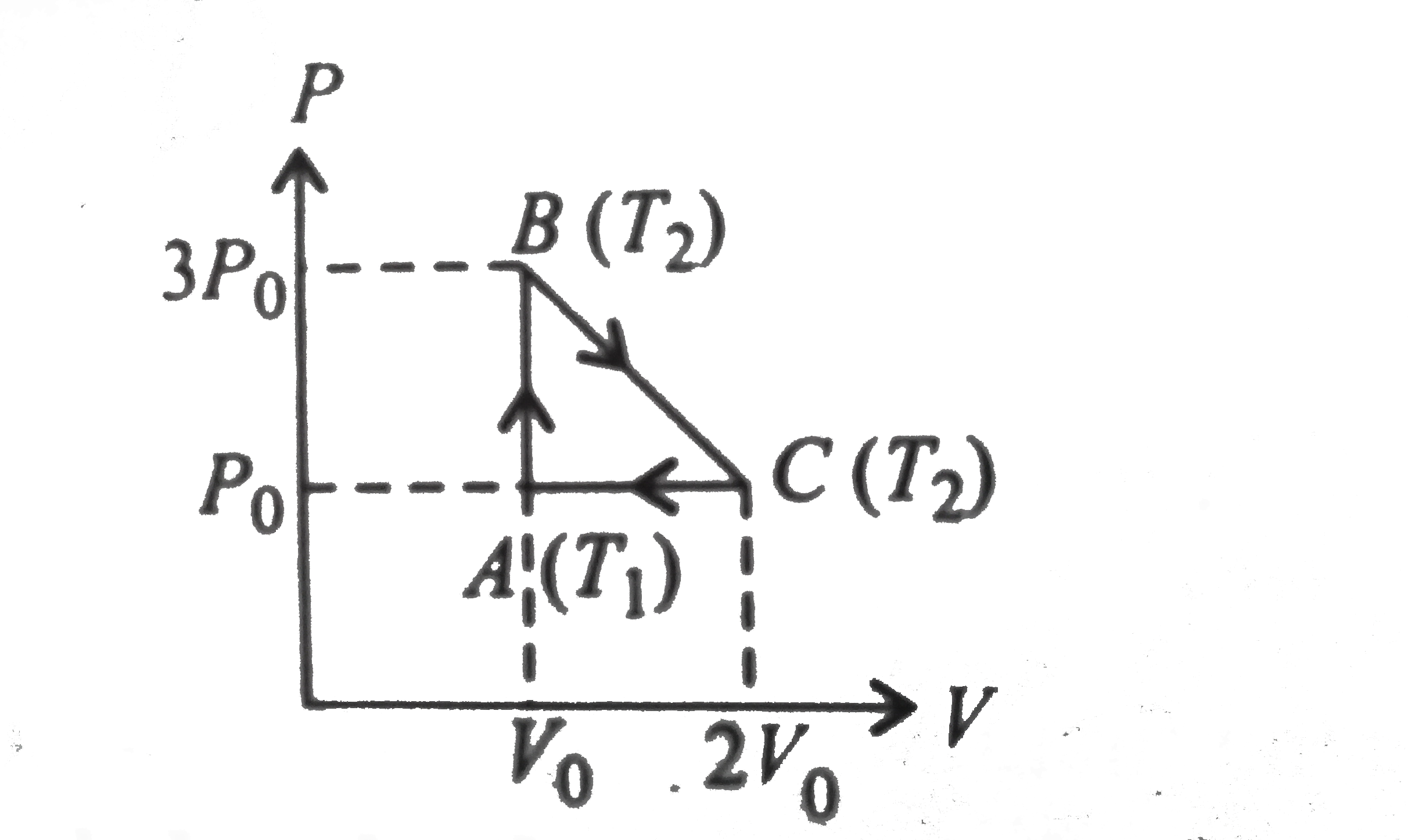
View SolutionOne mole of an ideal monatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate
(a) the work done by the gas.
(b) the heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB,
(c) the net heat absorbed by the gas in the path BC,
(d) the maximum temperature attained by the gas during the cycle.
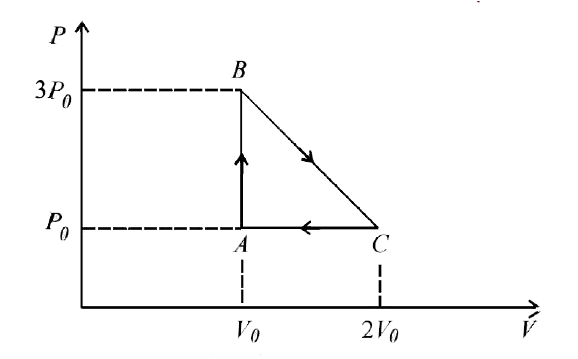
View SolutionOne mole of an ideal monatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate
(a) the work done by the gas.
(b) the heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB,
(c) the net heat absorbed by the gas in the path BC,
(d) the maximum temperature attained by the gas during the cycle.
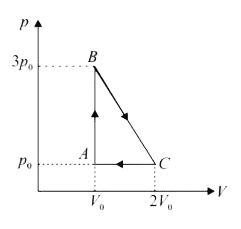
View SolutionOne mole of an ideal monoatomatic gas is taken round the cylic process ABCA as shown Then
View SolutionOne mole of ideal monoatomic gas is taken round the cyclic process as shown in figure.
The heat rejected by the gas in the path CA is ………...and the heat absorbed by the gas in the path AB is ………...........
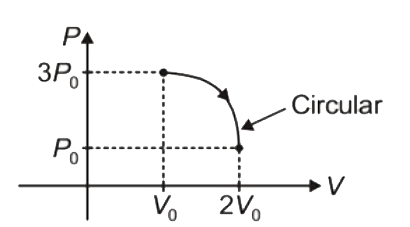
View SolutionOne mole of an ideal diatomic gas is taken through a process whose P−V diagram is shown in the figure. The work done by the gas is
View SolutionA sample of an ideal monoatomic gas is taken round the cycle ABCA as shown in the figure the work done during the cycle is

View SolutionOne mole of ideal monoatmic gas is carried throught the reversible cyclic process as shown in figure. Calculate net heat absorbed by the gas in the path BC

View Solution4 millimoles of an ideal monoatomic gas is taken through a cyclic process ABCDA, is shown in the figure, AB and CD are two isothermal curves having temperature 300 K and 600 K respectively. The total work done by the gas during the cyclic process is xRloge25. find the value of x
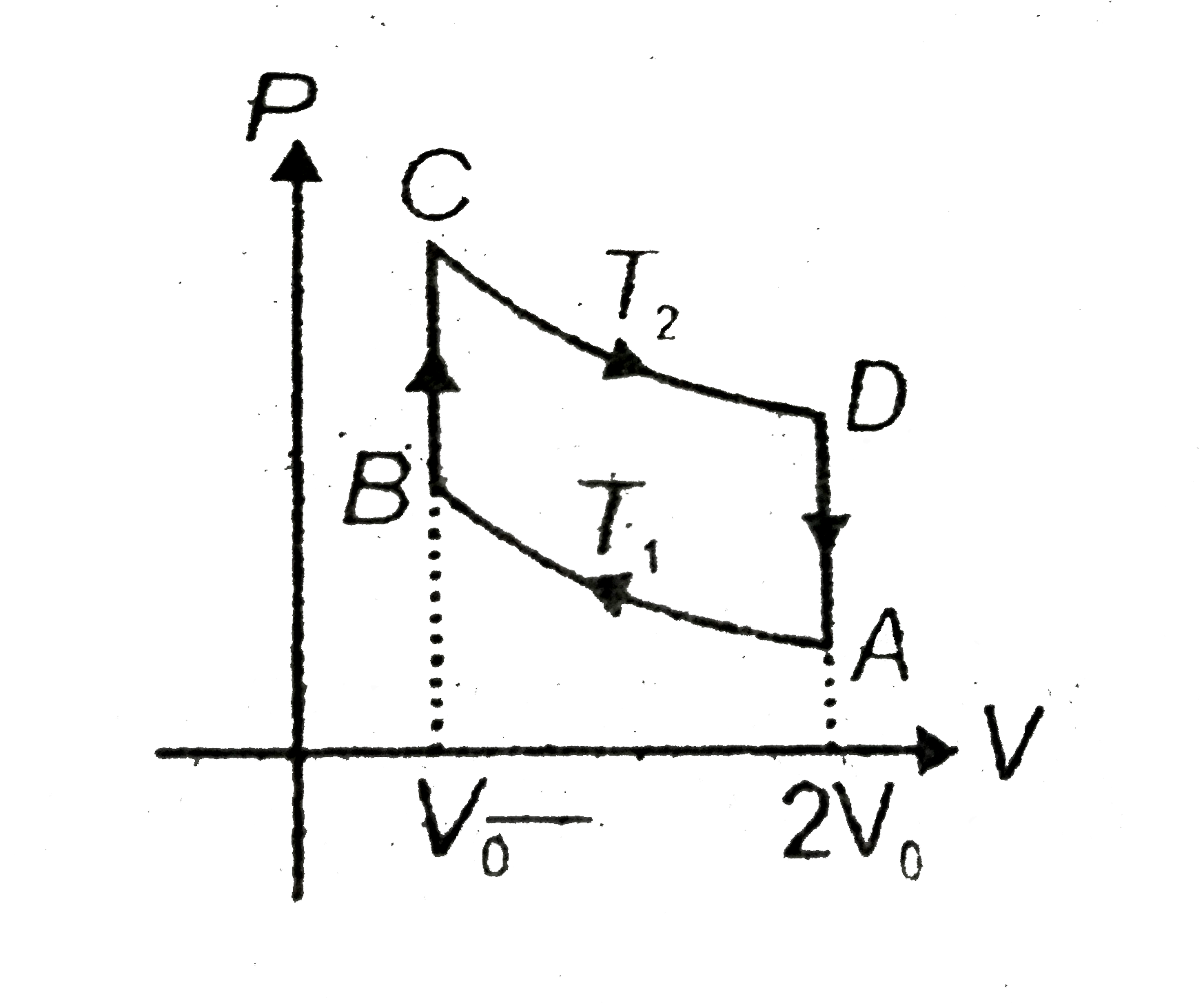 .
.
View Solution