Figure demonstrates a polytropic process (i.e.PVn = constant ) for an ideal gas. The work done by the gas be in the process AB is
_S01_086_Q01.png)
152P0V0
143P0V0
8P0V0
Insufficient information
The correct Answer is:B
For a polytropic process PVn = constant ⇒16P0Vn0=P0(2V0)n⇒n=4
Work done =P1V1−P2V2n−1=16P0V0−P0(2V0)4−1=143P0V0
Topper's Solved these Questions
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -01
Explore 65 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:EXERCISE -02
Explore 82 Videos
- GEOMETRICAL OPTICSBook:ALLENChapter:GEOMETRICAL OPTICSExercise:subjective
Explore 14 Videos
- CURRENT ELECTRICITYBook:ALLENChapter:CURRENT ELECTRICITYExercise:EX.II
Explore 66 Videos
- GRAVITATIONBook:ALLENChapter:GRAVITATIONExercise:EXERCISE 4
Explore 9 Videos
Similar Questions
Find the work done by the gas in the process ABC.
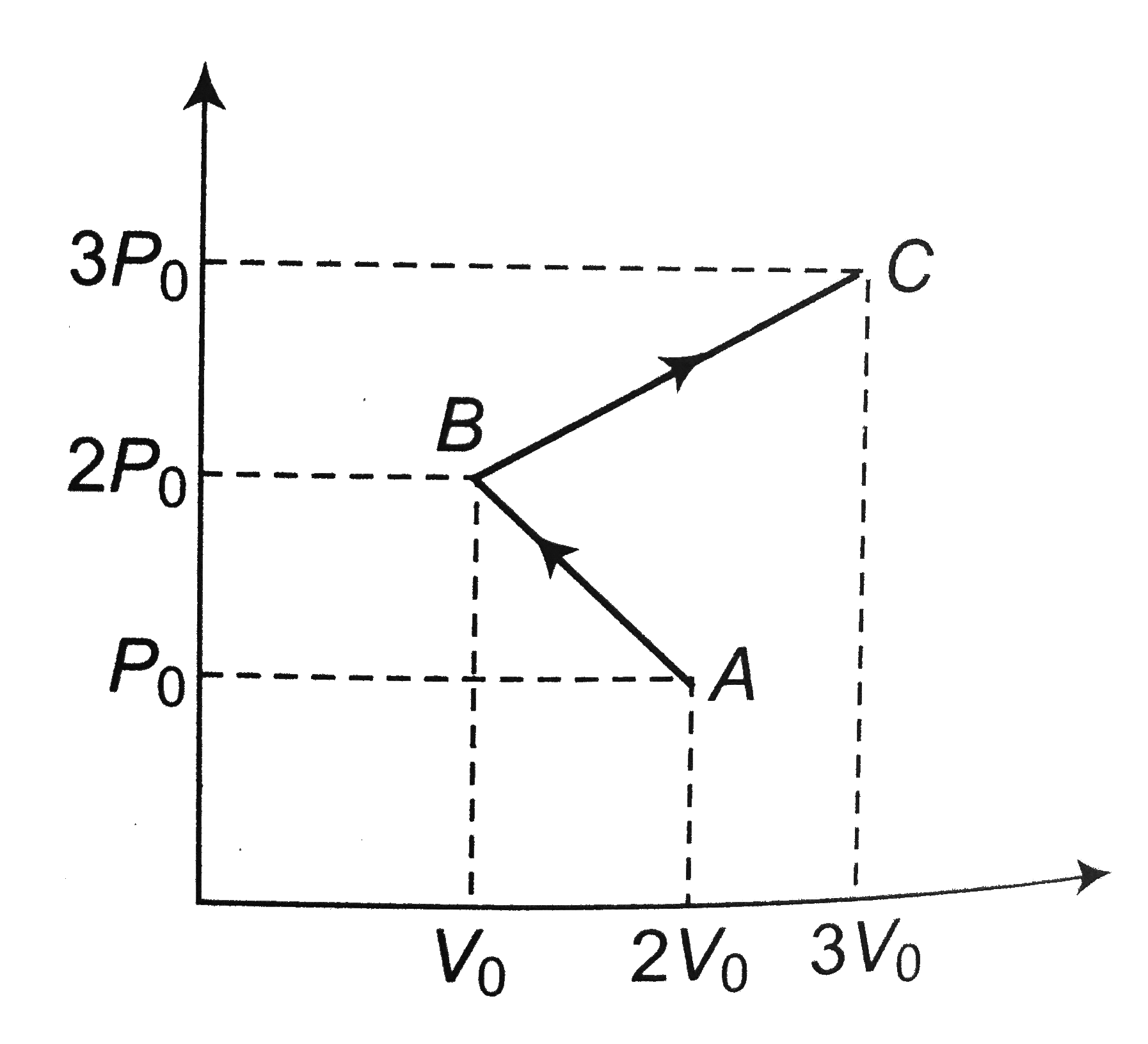
View SolutionFind work done by the gas in the process shown in figure.

View SolutionFind work done by the gas in the process shown in figure.

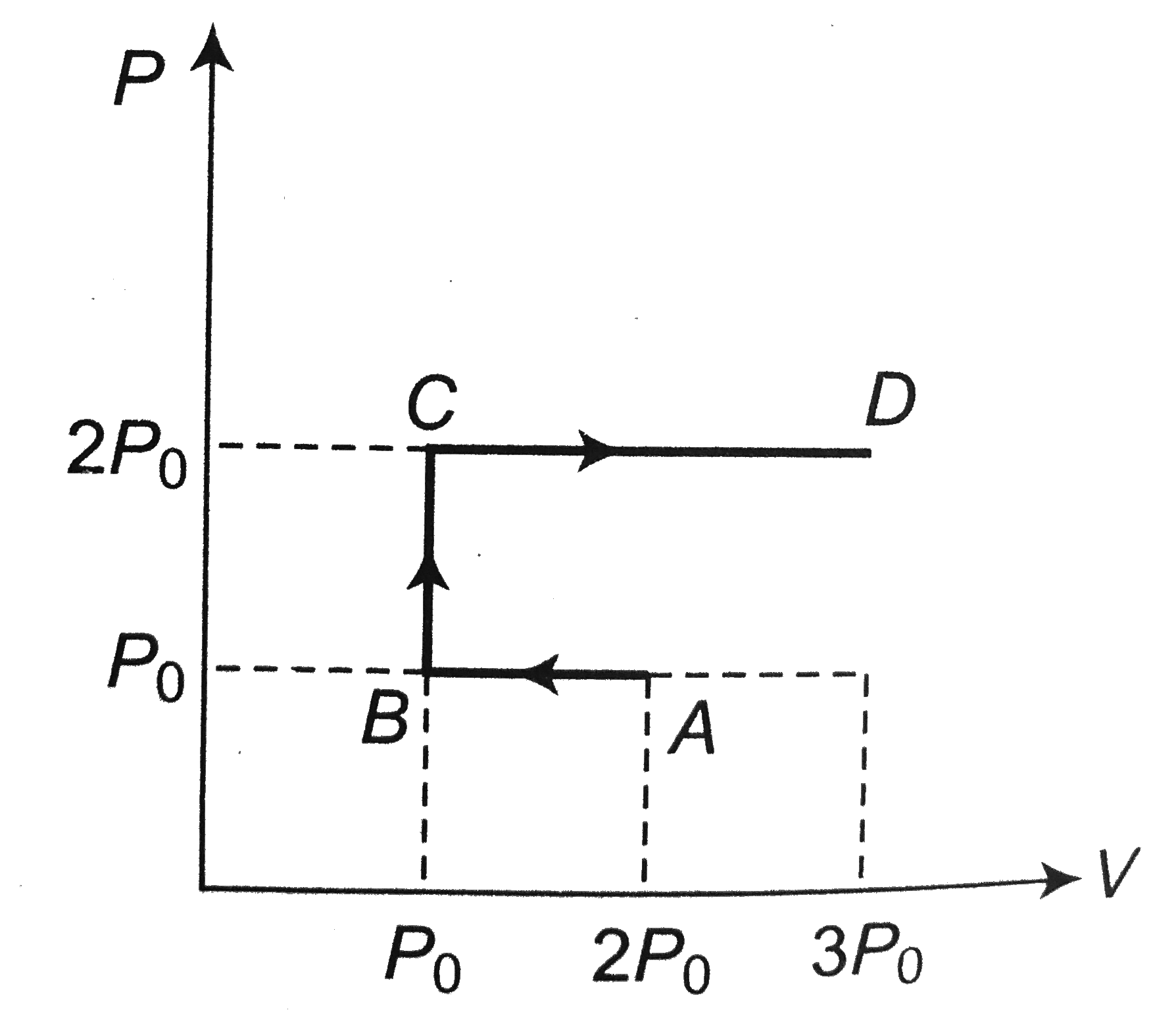
View SolutionP-V diagram of an ideal gas is as shown in figure. Work done by the gas in the process ABCD is
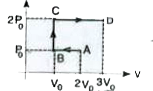
View SolutionP−V diagram of an ideal gas is as shown in figure. Work done by the gas in process ABCD is
View SolutionFor polytropic process PVn = constant, molar heat capacity (Cm) of an ideal gas is given by:
View SolutionP – V graph of an ideal gas is as shown in the diagram . Work done by the gas in the process ABCD is
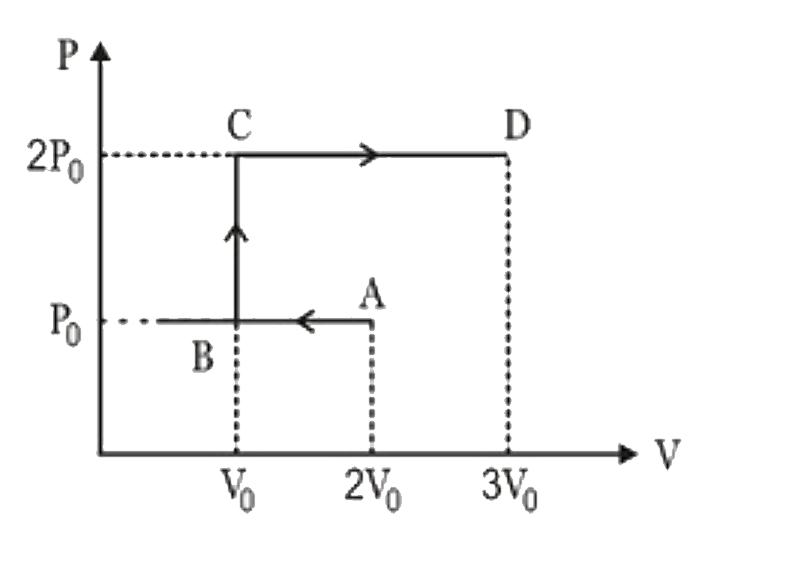
View SolutionOne mole of an ideal gas has an interal energy given by U=U0+2PV , where P is the pressure and V the volume of the gas. U0 is a constant. This gas undergoes the quasi− static cyclic process ABCD as shown in the U−V diagram. The work done by the ideal gas in the process AB is

View SolutionFind work done by the gas in the process AB shown in the following figures.
View Solutionan ideal diatomic gas undergoes a polytropic process described by the equation P√V=constant . The molar heat capacity of the gas during this process is
View Solution

