A block of mass 2 kg is placed on the floor . The coefficient of static friction is 0.4 . If a force of 2.8 N is applied on the block parallel to floor , the force of friction between the block and floor is : (Taking g = 10m/s2)
2.8N
8N
2.0N
zero
The correct Answer is:A
To solve the problem, we need to determine the force of friction acting on the block when a force is applied. Here’s a step-by-step breakdown of the solution:
Step 1: Calculate the weight of the block
The weight (W) of the block can be calculated using the formula:
W=m⋅g
where:
- m=2kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
Substituting the values:
W=2kg⋅10m/s2=20N
Step 2: Calculate the normal force (N)
Since the block is on a horizontal surface and there are no vertical forces acting other than its weight and the normal force, the normal force (N) is equal to the weight of the block:
N=W=20N
Step 3: Calculate the limiting friction (F_friction)
The limiting friction can be calculated using the formula:
Ffriction=μ⋅N
where:
- μ=0.4 (coefficient of static friction)
Substituting the values:
Ffriction=0.4⋅20N=8N
Step 4: Compare applied force with limiting friction
The applied force (F_applied) is given as:
Fapplied=2.8N
Now, we compare the applied force with the limiting friction:
- Limiting friction = 8 N
- Applied force = 2.8 N
Since the applied force (2.8 N) is less than the limiting friction (8 N), the block will not move.
Step 5: Determine the force of friction
When the block is not moving, the force of friction will be equal to the applied force (as it opposes the motion). Therefore, the force of friction is:
Ffriction=Fapplied=2.8N
Final Answer
The force of friction between the block and the floor is 2.8 N.
---
The weight (W) of the block can be calculated using the formula:
W=m⋅g
where:
- m=2kg (mass of the block)
- g=10m/s2 (acceleration due to gravity)
W=2kg⋅10m/s2=20N
Since the block is on a horizontal surface and there are no vertical forces acting other than its weight and the normal force, the normal force (N) is equal to the weight of the block:
N=W=20N
The limiting friction can be calculated using the formula:
Ffriction=μ⋅N
where:
- μ=0.4 (coefficient of static friction)
Ffriction=0.4⋅20N=8N
The applied force (F_applied) is given as:
Fapplied=2.8N
- Limiting friction = 8 N
- Applied force = 2.8 N
When the block is not moving, the force of friction will be equal to the applied force (as it opposes the motion). Therefore, the force of friction is:
Ffriction=Fapplied=2.8N
The force of friction between the block and the floor is 2.8 N.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-I
Explore 52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
Similar Questions
A block of mass 4 kg is kept on a rough horizontal surface. The coefficient of static friction is 0.8. If a forace of 19 N is applied on the block parallel to the floor, then the force of friction between the block and floor is
View SolutionA block of mass 2 kg is placed on the floor. The coefficient of static friction it 0.4. A force F of 2.5 N is applied on the block, as shown. calculate the force of friction between the block and the floor. (g=9.8m/s2).
View Solution
Knowledge Check
A block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 3 N is applied on the block as shown in figure. The force of friction between the block and the floor is (Take g=10ms−2)
 A3 NB8 NC4 ND6 N
A3 NB8 NC4 ND6 NA block of mass 2 kg is placed on the floor. The coefficient of static friction is 0.4. A force F of 2.5 N is applied on the block as shown in Fig. 15.4.4. The force of friction between the block and the floor is (g=9.8m/s2)
 A1.5 NB0.5 NC2.5 NDNone of the above
A1.5 NB0.5 NC2.5 NDNone of the above
A block of mass 2 kg is at rest on a floor . The coefficient of static friction between block and the floor is 0.54. A horizonatl force of 2.8 N is applied to the block . What should be the frictional force between the block and the floor ? ( take , g=10m/s2)
View SolutionA crate of mass 100 kg rests on the floor. The coefficient of static friction is 0.4. If a force of 250 N(parallel to the floor) is applied to the create, what's the magnitude of the force of static friction on the crate ?
View SolutionA block is lying static on the floor. The maximum value of static fictional force on the block is 10 N. If a horizontal force of 6 N is applied to the block,what will be the frictional force on the block?
View SolutionA block of mass'm' is resting on the floor of a lift. The coefficient of friction between the block and the floor is μ. When the lift is falling freely, the limiting frictional force between block and surface is
View SolutionA block of mass 1 kg is placed on a truck which accelerates with acceleration 5ms−2. The coefficient of static friction between the block and truck is 0.6. The frictional force acting on the block is
View SolutionA slab of 40kg lying on a frictionales floor and a block of 10 kg rests on the slab as shown in the figure. The coefficients of static and kinetic friction between the slab and the block are 0.6 and 0.4 respectively. If a force of 100N is applied on the block, then the acceleration the slab will be (g=10m/s2)
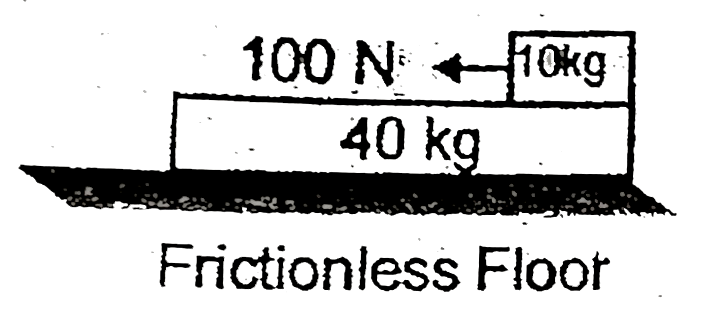
View Solution

