A passenger on a large ship sailing in a quiet sea hangs a ball from the celling of her cabin by means of a long thread. Whenever the ship acceleration when the pendulum stands at an angle of 5∘ to the vertical ?
To solve the problem of finding the acceleration of the ship when the pendulum hangs at an angle of 5 degrees to the vertical, we can follow these steps:
1. Understanding the Forces:
- When the ship accelerates, the pendulum bob will not hang vertically but will instead make an angle with the vertical. The forces acting on the bob are:
- The gravitational force (weight) acting downwards, mg.
- The tension in the thread, T, acting along the thread.
- A pseudo force ma acting horizontally backward due to the ship's acceleration a.
2. Setting Up the Coordinate System:
- Let the angle the pendulum makes with the vertical be θ=5∘.
- The tension T can be resolved into two components:
- Tcos(5∘) acting vertically upwards.
- Tsin(5∘) acting horizontally towards the back of the ship.
3. Applying Newton's Second Law:
- Since the pendulum is in equilibrium in the vertical direction:
Tcos(5∘)=mg(1)
- In the horizontal direction, the net force is equal to the pseudo force:
Tsin(5∘)=ma(2)
4. Dividing the Equations:
- To eliminate T, we can divide equation (2) by equation (1):
Tsin(5∘)Tcos(5∘)=mamg
- This simplifies to:
tan(5∘)=ag
5. Solving for Acceleration:
- Rearranging the equation gives:
a=gtan(5∘)
- Using g≈10m/s2 and calculating tan(5∘):
tan(5∘)≈0.0875
- Therefore:
a=10×0.0875=0.875m/s2
Final Answer:
The acceleration of the ship is 0.875m/s2.
---
- When the ship accelerates, the pendulum bob will not hang vertically but will instead make an angle with the vertical. The forces acting on the bob are:
- The gravitational force (weight) acting downwards, mg.
- The tension in the thread, T, acting along the thread.
- A pseudo force ma acting horizontally backward due to the ship's acceleration a.
- Let the angle the pendulum makes with the vertical be θ=5∘.
- The tension T can be resolved into two components:
- Tcos(5∘) acting vertically upwards.
- Tsin(5∘) acting horizontally towards the back of the ship.
- Since the pendulum is in equilibrium in the vertical direction:
Tcos(5∘)=mg(1)
- In the horizontal direction, the net force is equal to the pseudo force:
Tsin(5∘)=ma(2)
- To eliminate T, we can divide equation (2) by equation (1):
Tsin(5∘)Tcos(5∘)=mamg
- This simplifies to:
tan(5∘)=ag
- Rearranging the equation gives:
a=gtan(5∘)
- Using g≈10m/s2 and calculating tan(5∘):
tan(5∘)≈0.0875
- Therefore:
a=10×0.0875=0.875m/s2
The acceleration of the ship is 0.875m/s2.
Topper's Solved these Questions
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:SWOE
Explore 44 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-I
Explore 52 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- RACEBook:ALLENChapter:RACEExercise:Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
Explore 24 Videos
Similar Questions
A pendulum having a bob of mas m is hanging in a ship sailing along the equator from east to west. When the ship is stationary with respect to water the tension in the string is T0. a. Find the speed of the ship due to rotation of the earth about its axis. b. find the difference between T0 and the earth's attraction on the bob. c. If the ship sails at speed v, what is the tension in the string ? Angular speed of earth's rotation is ω and radius of the earth is R.
View SolutionOne end of a 10 cm long silk thread is fixed to a large vertical surface of a charged non-conducting plate and the other end is fastened to a small ball of mass 10 g and charge of 4×10−6C. In equilibrium, thread makes an angle of 60o with the vertical.
(a) Find the tension in the string in equilibrium.
(b) Suppose the ball is slightly pushed aside and released. Find the time period of the small oscillations.
(Use σ=7.5×10−7Cm2)
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If the angle the cannot makes with the horiaontal is increased from 45∘, the hoop will have to be
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.
A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.
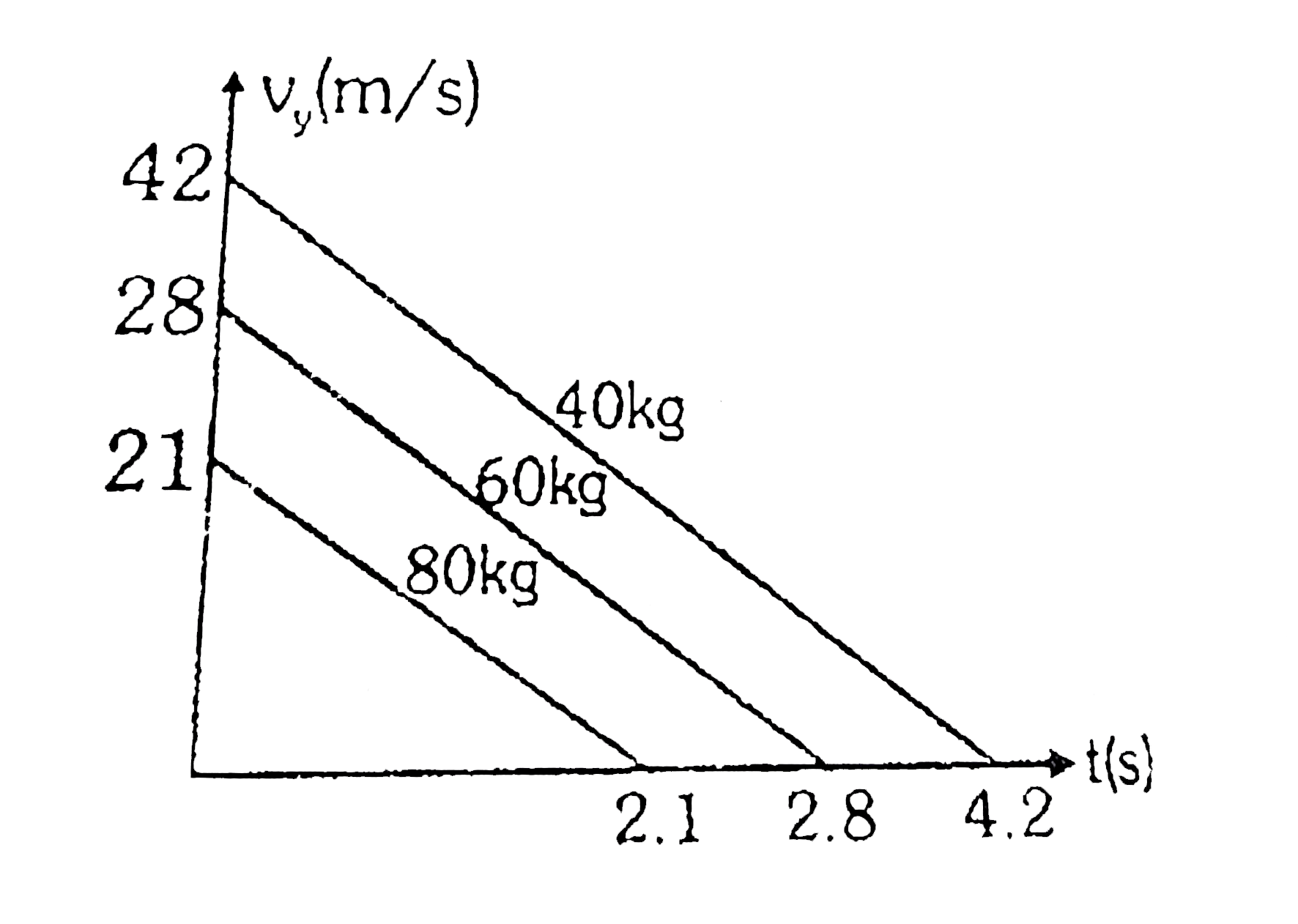
From figure 2, approximately how much time will it take for clown with a mass of 60 kg to reach the safety net located 10m below the height of the cannot?
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If the clown's mass is 80kg, what initial velocity v0 will have as he leaves the cannot?
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If the mass of a clown doubles, his initial kinetic energy, mv20/2, will :-
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If a clown holds on to hoop instead of passing through it, what is the position of the cable so that he doesn't hit his head on the ceiling as he swings upward?
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

The slope of the line segments plotted in figure 2 is a figure constant. Which one of the following physical quantities does this slope represent?
View SolutionA ballistic pendulum is a device that was used to measure the speeds of bullets before the development of electronic tiring, devices. The device consists of a large block of wood of mass M, hanging from two long cords. A bullet of mass m is fired into the block. the bullet comes quickly into rest and the block + bullet rises to a vertical distance h before the pendulum comes momentarily to rest as the ends of the arc. ltbr> In the process. the linear momentum is conserved. In such a collision. some kinetic energy is dissipated as heat: so mechanical energy is not conserved. When there is a loss in mechanical energy, the collision is said to be inelastic. Further when two bodies coalesce, the collision is said to be perfectly inelastic.

The energy dissipated as heat in the collision is
View SolutionA ballistic pendulum is a device that was used to measure the speeds of bullets before the development of electronic tiring, devices. The device consists of a large block of wood of mass M, hanging from two long cords. A bullet of mass m is fired into the block. the bullet comes quickly into rest and the block + bullet rises to a vertical distance h before the pendulum comes momentarily to rest as the ends of the arc. ltbr> In the process. the linear momentum is conserved. In such a collision. some kinetic energy is dissipated as heat: so mechanical energy is not conserved. When there is a loss in mechanical energy, the collision is said to be inelastic. Further when two bodies coalesce, the collision is said to be perfectly inelastic.

The collision of block-bullet system is
View Solution