[" 12.A stationary man observes that the rain strikes him at an angle of "60^(@)],[" to the horizontal.When he begins to move with a velocity of "25m/sec" ,"],[" then the drops appear to strike him at an angle "30^(@)" from horizontal."],[" Calculate the velocity of the rain drops."],[" Ans."25m/sec" ."]
To solve the problem step-by-step, we will analyze the situation involving the stationary observer and the moving observer in the context of the rain's velocity.
Step 1: Understand the Given Information
- A stationary man observes rain striking him at an angle of 60∘ to the horizontal.
- When the man moves with a velocity of 25m/s, the rain appears to strike him at an angle of 30∘ to the horizontal.
Step 2: Set Up the Velocity Components
Let vr be the velocity of the rain drops. We can break this velocity into horizontal and vertical components:
- The horizontal component of the rain's velocity, vrh=vrcos(60∘)=vr⋅12=vr2.
- The vertical component of the rain's velocity, vrv=vrsin(60∘)=vr⋅√32.
Step 3: Analyze the Situation When the Man is Moving
When the man moves with a velocity of 25m/s, the effective horizontal velocity of the rain relative to him is:
v′rh=vrh+25=vr2+25
The vertical component remains the same:
v′rv=vrv=√32vr
Step 4: Set Up the Tangent Relationship for the Moving Observer
For the moving observer, the angle at which the rain strikes him is 30∘. Thus, we can write:
tan(30∘)=v′rvv′rh
Substituting the values we have:
tan(30∘)=√32vrvr2+25
Since tan(30∘)=1√3, we can set up the equation:
1√3=√32vrvr2+25
Step 5: Cross-Multiply to Solve for vr
Cross-multiplying gives us:
(1√3)(vr2+25)=√32vr
Expanding this:
vr2√3+25√3=√32vr
Step 6: Rearranging the Equation
Multiply through by 2√3 to eliminate the fraction:
vr+50=3vr
Rearranging gives:
50=3vr−vr
50=2vr
Step 7: Solve for vr
Dividing both sides by 2:
vr=25m/s
Final Answer
The velocity of the rain drops is 25m/s.
---
- A stationary man observes rain striking him at an angle of 60∘ to the horizontal.
- When the man moves with a velocity of 25m/s, the rain appears to strike him at an angle of 30∘ to the horizontal.
Let vr be the velocity of the rain drops. We can break this velocity into horizontal and vertical components:
- The horizontal component of the rain's velocity, vrh=vrcos(60∘)=vr⋅12=vr2.
- The vertical component of the rain's velocity, vrv=vrsin(60∘)=vr⋅√32.
When the man moves with a velocity of 25m/s, the effective horizontal velocity of the rain relative to him is:
v′rh=vrh+25=vr2+25
The vertical component remains the same:
v′rv=vrv=√32vr
For the moving observer, the angle at which the rain strikes him is 30∘. Thus, we can write:
tan(30∘)=v′rvv′rh
Substituting the values we have:
tan(30∘)=√32vrvr2+25
Since tan(30∘)=1√3, we can set up the equation:
1√3=√32vrvr2+25
Cross-multiplying gives us:
(1√3)(vr2+25)=√32vr
Expanding this:
vr2√3+25√3=√32vr
Multiply through by 2√3 to eliminate the fraction:
vr+50=3vr
Rearranging gives:
50=3vr−vr
50=2vr
Dividing both sides by 2:
vr=25m/s
The velocity of the rain drops is 25m/s.
Similar Questions
A girl waking on a road in rain which is falling down vertically holds her umbrella at an angle of 60∘ to the horizontal.The ratio of the velocity of the rain and girl is
View SolutionA man moving with a velocity of 5m/s on a horizontal road observes that raindrops fall at an angle of 45∘ with the vertical. When he moves with a velocity of 16m/s along an inclined plane, which is inclined at 30∘ with the horizontal , he observes raindrops falling vertically downward as shown in the figure. Find the actual velocity of the raindrops.
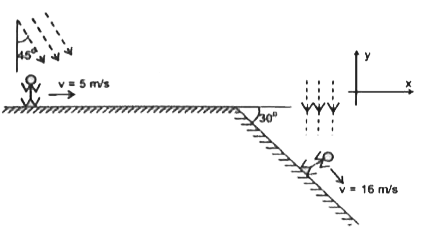
View Solution
Knowledge Check
A man walks in rain with a velocity of 5 kmph. The rain drops strike at him at an angle of 45∘ with the horizontal. The downward velocity of the rain drops will be :
A5 kphB4 kphC3 kphD1 kphA man moves on a cycle with a velocity of 4 km/hr. The rain appears to fall on him with a velocity of 3 km/hr vertically. The actual velocity of the rain is
A7 km/hrB5 km/hrC4/3 km/hrD3/4 km/hrA man walks in rain with a velocity of 5 kph. The rain drops strike at him at an angle of 45∘ with the horizontal. The downward velocity of the rain drops will be :
A5 kmh−1B4 kmh−1C3 kmh−1D1 kmh−1
A body is thrown at an angle 30∘ to the horizontal with the velocity of 30m/ After 1 sec. its velocity will be ("in"m//s) (g=10m/s2)
View SolutionWhen a boy is stationary, he observes that rain drops are falling at 30∘ to vertical direction. When he starts running with speed 10ms, he observed that rain drops are falling vertically downwards. Calculate the actual velocity of rain drops.
View SolutionA stationary man observes that the rain is falling vertically downwards. When he starts running a velocity of 12kmh−1, he observes that the rain is falling at an angle 60∘ with the vertical. The actual velocity of rain is
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionA stone is thrown from a bridge at an angle of 30º down with the horizontal with a velocity of 25 m/s. If the stone strikes the water after 2.5 sec then calculate the height of the bridge from the water surface-
View Solution
