How many orbitals are possible for n = 3, l=2 ?
1
3
5
7
The correct Answer is:C
To determine how many orbitals are possible for n = 3 and l = 2, we can follow these steps:
1. Identify the Quantum Numbers:
- The principal quantum number (n) is given as 3.
- The azimuthal quantum number (l) is given as 2.
2. Understand the Relationship Between n and l:
- The value of l can range from 0 to (n-1). Therefore, for n = 3, l can take the values 0, 1, or 2.
- The corresponding subshells for these values of l are:
- l = 0 corresponds to the s subshell (3s).
- l = 1 corresponds to the p subshell (3p).
- l = 2 corresponds to the d subshell (3d).
3. Determine the Number of Orbitals:
- The number of orbitals in a subshell can be calculated using the formula:
Number of orbitals=2l+1
- Substitute the value of l into the formula:
Number of orbitals=2(2)+1=4+1=5
4. Conclusion:
- Therefore, for n = 3 and l = 2, there are 5 orbitals in the d subshell.
Final Answer:
There are 5 orbitals possible for n = 3 and l = 2.
- The principal quantum number (n) is given as 3.
- The azimuthal quantum number (l) is given as 2.
- The value of l can range from 0 to (n-1). Therefore, for n = 3, l can take the values 0, 1, or 2.
- The corresponding subshells for these values of l are:
- l = 0 corresponds to the s subshell (3s).
- l = 1 corresponds to the p subshell (3p).
- l = 2 corresponds to the d subshell (3d).
- The number of orbitals in a subshell can be calculated using the formula:
Number of orbitals=2l+1
- Substitute the value of l into the formula:
Number of orbitals=2(2)+1=4+1=5
- Therefore, for n = 3 and l = 2, there are 5 orbitals in the d subshell.
There are 5 orbitals possible for n = 3 and l = 2.
Topper's Solved these Questions
- CHEMISTRY AT A GLANCEBook:ALLENChapter:CHEMISTRY AT A GLANCEExercise:INORGANIC CHEMISTRY
Explore 300 Videos
- CHEMISTRY AT A GLANCEBook:ALLENChapter:CHEMISTRY AT A GLANCEExercise:ORGANIC CHEMISTRY
Explore 472 Videos
- Chemical EquilibriumBook:ALLENChapter:Chemical EquilibriumExercise:All Questions
Explore 30 Videos
- ELECTROCHEMISTRYBook:ALLENChapter:ELECTROCHEMISTRYExercise:EXERCISE -05 [B]
Explore 38 Videos
Similar Questions
n = 5 , ms=+12 How many orbitals are possible :
View SolutionHow many orbitals are possible in
5th energy level
View SolutionHow many orbitals are possible in
a. 4th energy level b. 5f sub-shell
View SolutionHow many stereoisomers are possible for
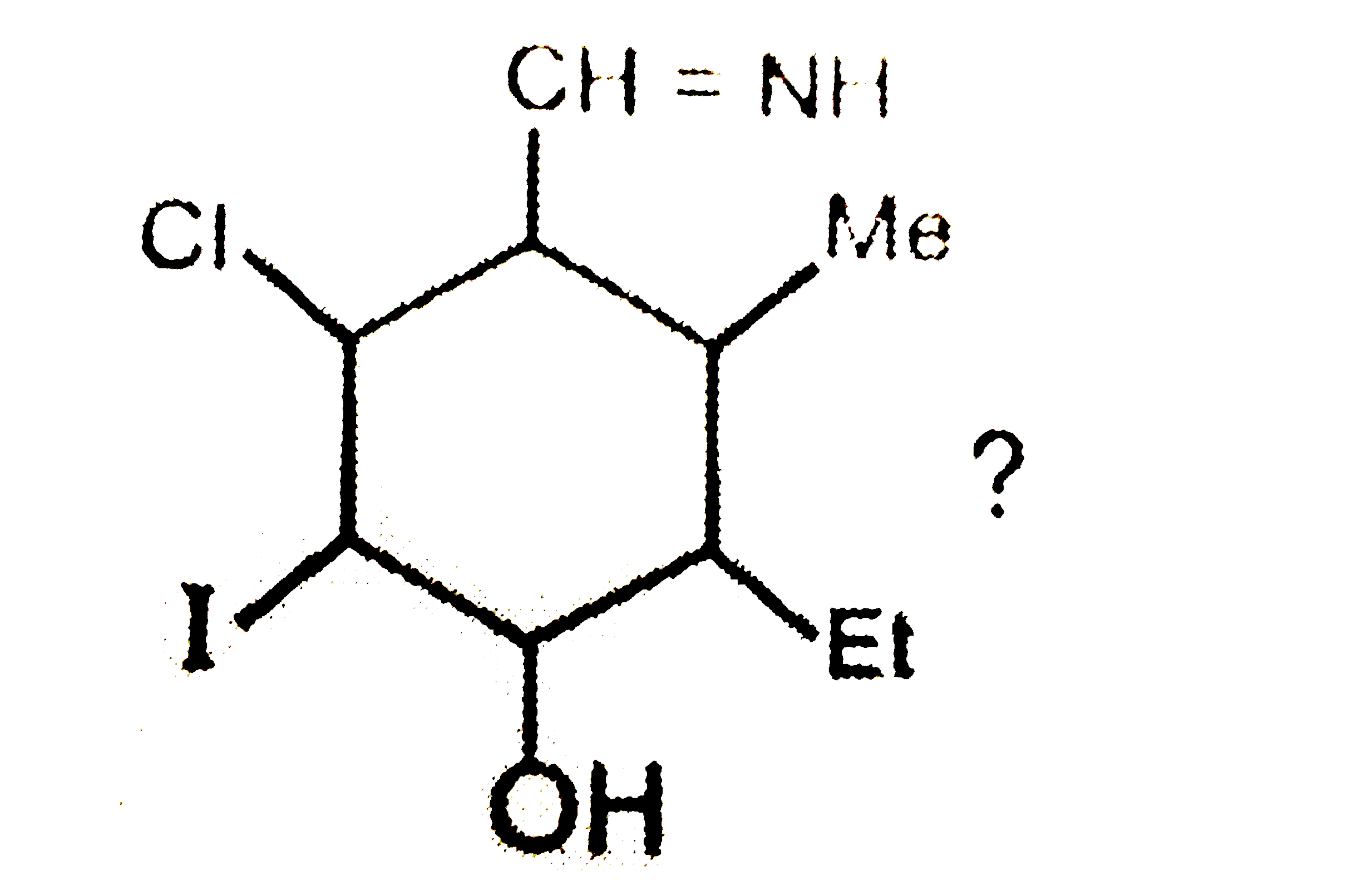
View SolutionHow many geometrical isomers are possible for

View SolutionWhat is a nodal plane ? How many nodal plance are possible for 2p and 3d - orbitals ?
View SolutionHow many geometrical isomers are possible for complex [Mab(AB)2]n±?
View SolutionHow many geometrical isomers are possible for [Zn(NH3)ClBrPPh3]− ?
View SolutionHow many isomers are possible for the complex ion [Cr(NH3)(OH)2Cl3]2− ?
View SolutionHow many geometrical isomers are possible for [Pd2+(NH2−CH(CH3)−CO−2)2]0
View Solution