How many geometrical isomers are possible for complex ?
5
4
3
6
The correct Answer is:A
To determine the number of geometrical isomers for the complex (Mab(AB)2)n+−, we need to analyze the coordination environment of the metal center (M) and the types of ligands involved.
1. Identify the Ligands:
- The complex contains one unidentate ligand (denoted as "a" and "b") and two bidentate ligands (denoted as "AB").
- The unidentate ligands can coordinate to the metal center at one site each, while the bidentate ligands can coordinate at two sites.
2. Determine the Coordination Geometry:
- Since there are two bidentate ligands and one unidentate ligand, the coordination number of the metal is 6.
- This typically leads to an octahedral geometry.
3. Analyze Possible Geometrical Isomers:
- In an octahedral complex, the arrangement of ligands can lead to different geometrical isomers, specifically cis and trans configurations.
- For the given complex (Mab(AB)2)n+−, we can have the following configurations:
- Cis Isomers: Where similar ligands are adjacent to each other.
- Trans Isomers: Where similar ligands are opposite to each other.
4. Draw Possible Isomers:
- Cis Isomers:
- Isomer 1: Ligands "a" and "b" are adjacent, and both "AB" ligands are adjacent.
- Isomer 2: Ligands "a" and "b" are adjacent, but the "AB" ligands are on opposite sides.
- Trans Isomers:
- Isomer 3: Ligands "a" and "b" are opposite, and both "AB" ligands are adjacent.
- Isomer 4: Ligands "a" and "b" are opposite, and the "AB" ligands are also opposite.
5. Count All Possible Isomers:
- After drawing and analyzing the configurations, we find that there are a total of 6 distinct geometrical isomers for the complex (Mab(AB)2)n+−.
Final Answer:
The total number of geometrical isomers possible for the complex (Mab(AB)2)n+− is 6.
- The complex contains one unidentate ligand (denoted as "a" and "b") and two bidentate ligands (denoted as "AB").
- The unidentate ligands can coordinate to the metal center at one site each, while the bidentate ligands can coordinate at two sites.
- Since there are two bidentate ligands and one unidentate ligand, the coordination number of the metal is 6.
- This typically leads to an octahedral geometry.
- In an octahedral complex, the arrangement of ligands can lead to different geometrical isomers, specifically cis and trans configurations.
- For the given complex (Mab(AB)2)n+−, we can have the following configurations:
- Cis Isomers: Where similar ligands are adjacent to each other.
- Trans Isomers: Where similar ligands are opposite to each other.
- Cis Isomers:
- Isomer 1: Ligands "a" and "b" are adjacent, and both "AB" ligands are adjacent.
- Isomer 2: Ligands "a" and "b" are adjacent, but the "AB" ligands are on opposite sides.
- Trans Isomers:
- Isomer 3: Ligands "a" and "b" are opposite, and both "AB" ligands are adjacent.
- Isomer 4: Ligands "a" and "b" are opposite, and the "AB" ligands are also opposite.
- After drawing and analyzing the configurations, we find that there are a total of 6 distinct geometrical isomers for the complex (Mab(AB)2)n+−.
The total number of geometrical isomers possible for the complex (Mab(AB)2)n+− is 6.
Topper's Solved these Questions
- CO-ORDINATION COMPOUNDSBook:VK JAISWAL ENGLISHChapter:CO-ORDINATION COMPOUNDSExercise:SUBJECTIVE PROBLEMS
Explore 42 Videos
- CHEMICAL BONDING (BASIC)Book:VK JAISWAL ENGLISHChapter:CHEMICAL BONDING (BASIC)Exercise:SUBJECTIVE PROBLEMS
Explore 54 Videos
- d-BLOCK ELEMENTSBook:VK JAISWAL ENGLISHChapter:d-BLOCK ELEMENTSExercise:ASSERTION-REASON TYPE QUESTIONS
Explore 32 Videos
Similar Questions
Knowledge Check
CH2=CH–CH=CH–CH=CH2
How many geometrical isomers are possible for this compound ?A2B3C4D8CH3−CH=C∣Br−C∣Cl−CH−CH3
How many geometrical isomers are possible for this compound?A2B3C4D6
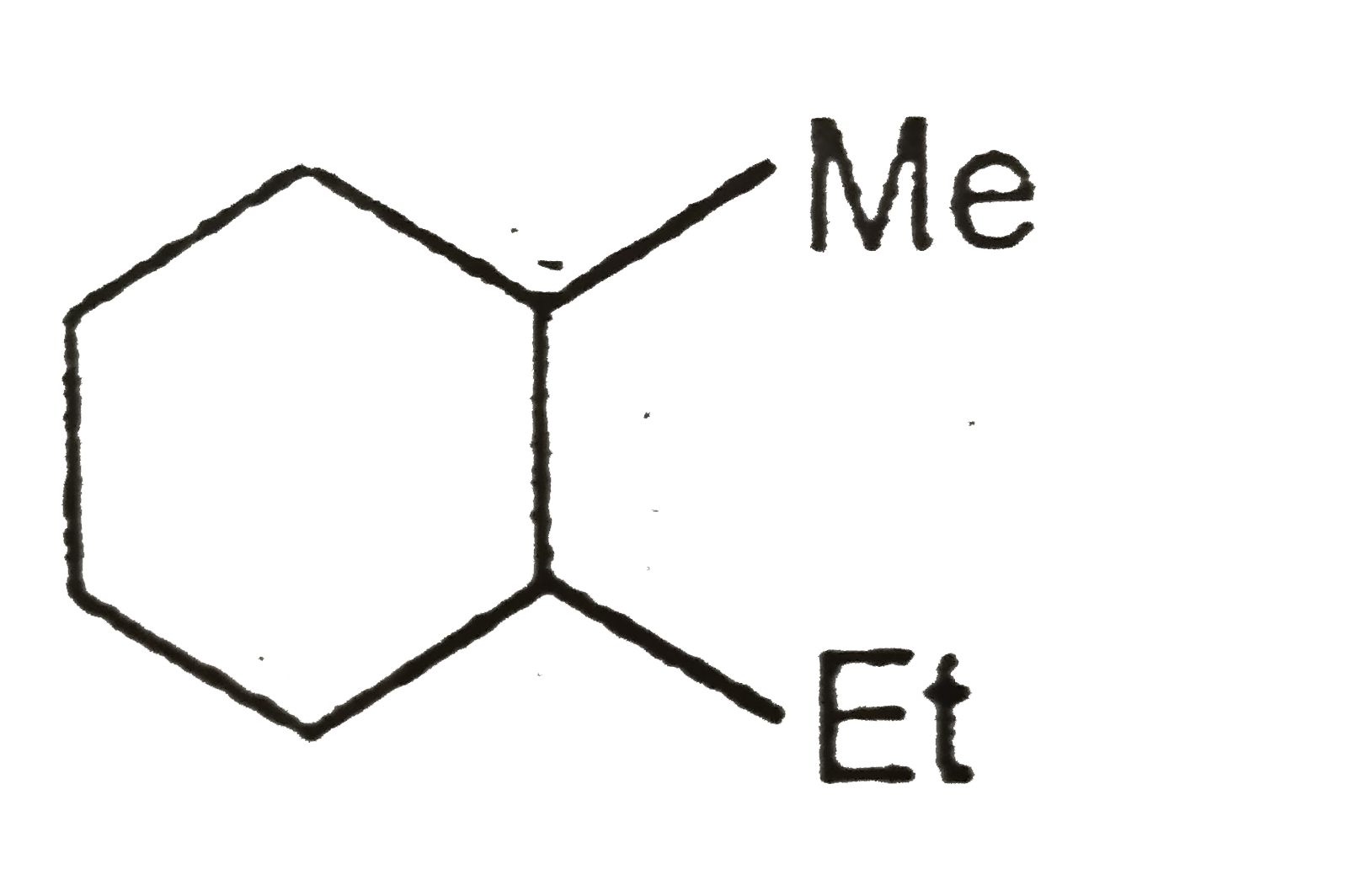
Number of geometrical isomers possible of
View SolutionHow many geometrical isomers are possible for [Zn(NH3)ClBrPPh3]− ?
View SolutionHow many positional isomers are possible for this compound
View SolutionHow many position isomers are possible for chlorophenol?
View SolutionHow many geometrical isomers are possible [Co(acac)2BrCl]Θ are:
View SolutionHow many geometrical isomers are possible [Co(acac)2BrCl]Θ are:
View Solution