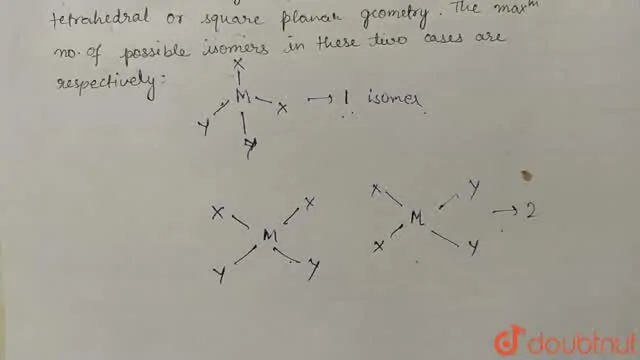
A coordination complex of type MX2Y2 (M-metal ion: X, Y-monodentate lingads), can have either a tetrahedral or a square planar geometry. The maximum number of posible isomers in these two cases are respectively:
1 and 2
2 and 1
1 and 3
3 and 2
The correct Answer is:A
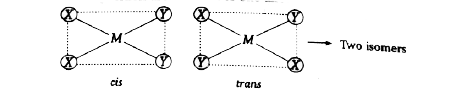
In tetrahedral all the posiiton are adjacent to one another hence only one isomer is possible
Related Playlists
- BOOK - VK JAISWAL ENGLISHCHAPTER - CO-ORDINATION COMPOUNDSEXERCISE - SUBJECTIVE PROBLEMS42videos
CO-ORDINATION COMPOUNDS
- BOOK - VK JAISWAL ENGLISHCHAPTER - CHEMICAL BONDING (BASIC)EXERCISE - SUBJECTIVE PROBLEMS54videos
CHEMICAL BONDING (BASIC)
- BOOK - VK JAISWAL ENGLISHCHAPTER - d-BLOCK ELEMENTSEXERCISE - ASSERTION-REASON TYPE QUESTIONS32videos
d-BLOCK ELEMENTS
Similar Questions
Nickel (Z=28) combines with a uninegative monodentate ligand X− to form a paramagnetic complex [NiX4]2−. The number of unpaired electron(s) in the nickel and geometry of this complex ion are, respectively:
View SolutionHomoleptic octahedral complexes of a metal ion 'M3+' with three monodentate ligands L1,L2 and L3 absorb wavelengths in the region of green, blue and red respectively. The increasing order of the ligand strength is :
View SolutionHomoleptic octahedral complexes of a metal ion 'M3+' with three monodentate ligands L1,L2 and L3 absorb wavelengths in the region of green, blue and red respectively. The increasing order of the ligand strength is :
View SolutionThe maximum number of electrons that can be accomoddated in dx2−y2 orbital is
View SolutionThe maximum number of electrons that can be accomoddated in dx2−y2 orbital is
View SolutionFor the square planar complex [M(a) (b) (c ) (d)] (where M = central metal and a, b, c and d are monodentate ligands), the number of possible geometrical isomers are
View SolutionVelence bond theroy describes the bonding in complexs in terms of coordinate -covalent bond resulting from overlap filled ligand orbitals with vacant metal hybrid orbitals This theory explains magnetic behaviour and geometrical shape of coordination compounds Magnetic moment of a complex compound can be determined experimentally and theoretically by using spin only formula
Magnetic moment √n(n+2)BM (where n = No. unpaired electrons) .
Ni2+ cation combines with a uninegative monodentate ligand XΘ to form paramagnetic complex [NiCI4]2− The number of unpaired electrons(s) in central metal cation and geometry of this complex respectively are
(a) One,tetrahedral
(b) Two,tetrahedral
(c ) One,square planar
(d) Two, square planar .View SolutionAssertion : Tetrahedral complexes having two different types of unidentate ligands coordinated with central metal ion will show geometrical isomerism .
Reason : Geometrical isomerism arises in homoleptic complexes due to different possible geometric arrangement of the ligands .View SolutionAn aqueous solution of metal ion MI reacts separately with reagents Q and R in excess to give tetrahedral and square planar complexes, respectively An aqueous solution of another metal ion M2 always forms tetrahedral complexs with theses reagents. Aqueous solution of M2 on reaction with reagent S gives white precipitate which dissolves in excess of S The reactions are summarised in the scheme given below: SCHEME :
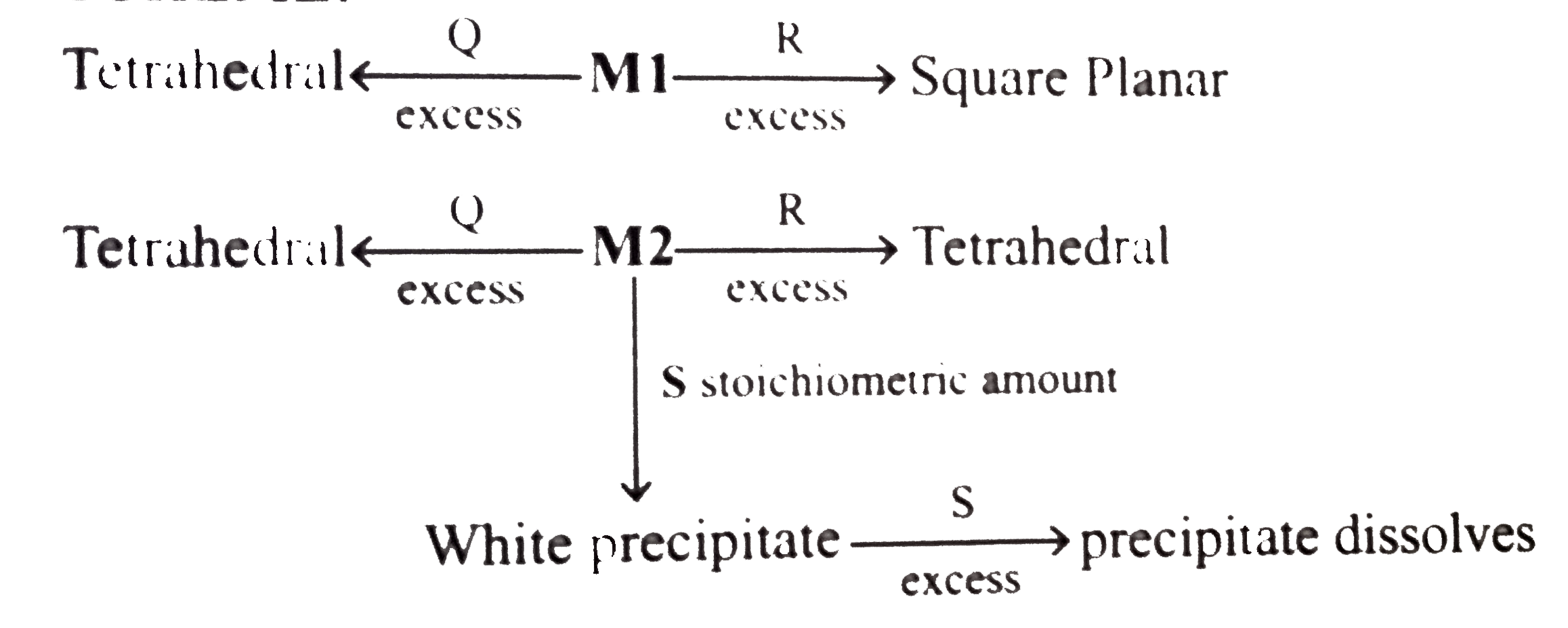
What is M2View SolutionA spinal is an important class of oxides consisting of two types of metal ions with oxides ions arranged in CCP layer. The normal spinal has one-eighth of the tetrahedral holes occupied by one type of metal ion and one-half of the octahedral holes occupied by another type of metal ion. such a spinal is formed by Zn2+,Al3+andO2− in the tetrahedral holes. if formula of the compound is ZnxAlyOz, then find the value of (x+y+z) ?
View Solution