The trajectory of a projectile in a vertical plane is .
![The trajectory of a projectile in a vertical plane is y=sqrt(3)x-2x^(2). [g=10 m//s^(2)] Angle of projection theta is :-](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_C02_E01_146_Q01.png)
Angle of projection is :-
rad
The correct Answer is:B
Trajectory equation is
&
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#43videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#56videos
KINEMATICS
- BOOK - ALLENCHAPTER - KINEMATICSEXERCISE - Comprehension#25videos
KINEMATICS
- BOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)22videos
ERROR AND MEASUREMENT
- BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-78videos
KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)
Similar Questions
The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
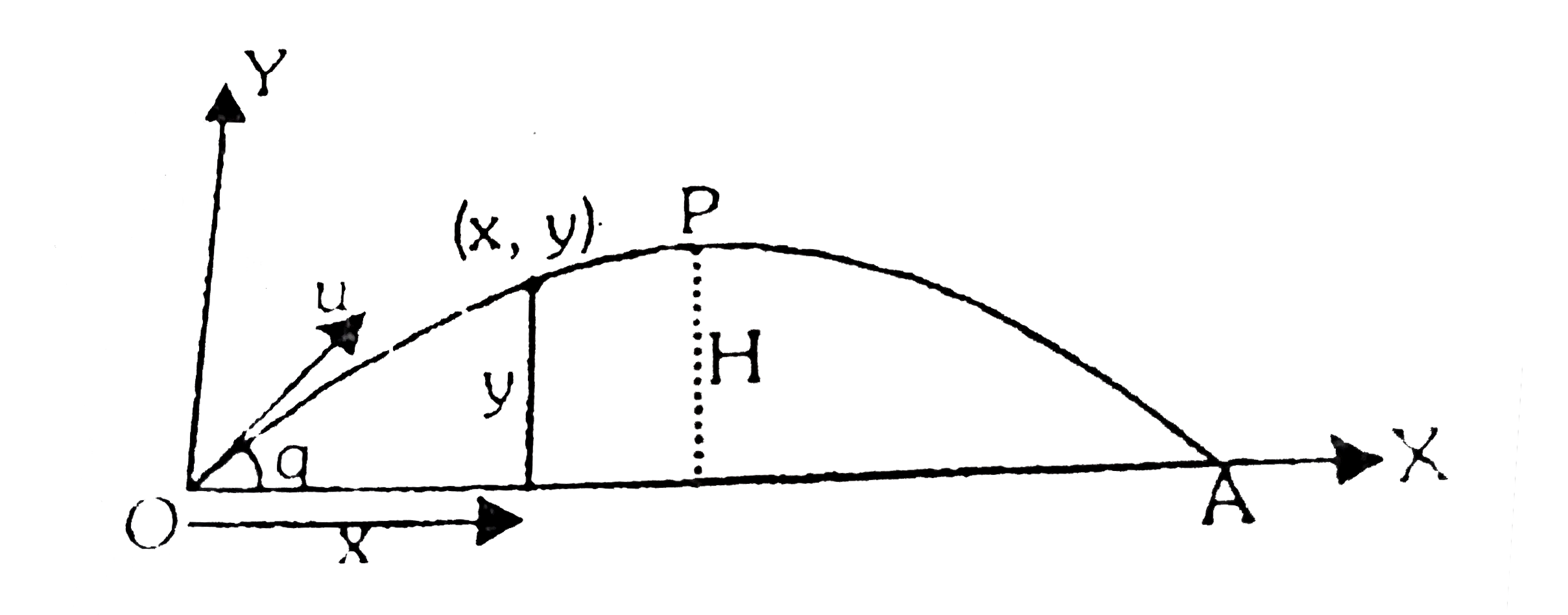
Range OA is :-View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
Time of flight of the projectile is :-View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
Maximum height H is :-View SolutionThe equation of a projectile is y=√3x−gx22
the angle of projection is:-View SolutionThe equation of trajectory of an oblique projectile y=√3x−gx22. The angle of projection is
View SolutionThe equation of trajectory ofa projectile is y=10x−59x2 If we assume g=10ms−2, the range of projectile (in metre) is
View SolutionThe trajectory of a projectile in a vertical plane is y=ax−bx2, where aandb are constant and xandy are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
View SolutionThe trajectory of a projectile in a vertical plane is y=ax−bx2, where aandb are constant and xandy are, respectively, horizontal and vertical distances of the projectile from the point of projection. The maximum height attained by the particle and the angle of projectile from the horizontal are.
View SolutionA particle is projected in x−y plane with y−axis along vertical, the point of projection being origin. The equation of projectile is y=√3x−gx22. The angle of projectile is ……………..and initial velocity is ………………… .
View SolutionA particle is projected in x−y plane with y−axis along vertical, the point of projection being origin. The equation of projectile is y=√3x−gx22. The angle of projectile is ……………..and initial velocity is ………………… .
View Solution