If the velocity of the particle is given by v=√x and initially particle was at x=4m then which of the following are correct.
At t=2s, the position of the particle is at x=9m
Particle acceleration at t=2s is 1m/s2
Particle acceleration is 1/2m/s2 through out the motion
Particle will never go in negative direction from it's starting position
The correct Answer is:A, C, D
To solve the problem step by step, we will analyze the given information and derive the necessary equations.
Step 1: Understand the relationship between velocity and position
The velocity of the particle is given by the equation:
v=√x
We know that velocity v can also be expressed as:
v=dxdt
Thus, we can equate the two expressions:
dxdt=√x
Step 2: Rearrange the equation for integration
Rearranging the equation gives:
dx=√xdt
To facilitate integration, we can express this as:
dx√x=dt
Step 3: Integrate both sides
Now, we will integrate both sides:
- The left side will be integrated from the initial position x=4 to x.
- The right side will be integrated from t=0 to t.
The integration gives:
∫x4dx√x=∫t0dt
Calculating the integrals:
- The left side:
2√x∣∣∣x4=2√x−4
- The right side:
t−0=t
Setting these equal gives us:
2√x−4=t
Step 4: Solve for x
Rearranging the equation:
2√x=t+4
√x=t+42
Squaring both sides yields:
x=(t+42)2
Step 5: Substitute t=2 seconds to find x
Now, we can substitute t=2 seconds into the equation:
x=(2+42)2=(62)2=32=9meters
Step 6: Determine the acceleration
To find the acceleration, we first need to find the velocity as a function of time:
From the expression for x:
x=(t+42)2
Differentiating x with respect to t:
v=dxdt=ddt(t+42)2=12⋅2(t+42)⋅12=t+42
Now, differentiating v with respect to t to find acceleration:
a=dvdt=12
Step 7: Analyze the results
1. At t=2 seconds, the position x=9 meters (Correct).
2. The acceleration a=12m/s2 (Incorrect statement in the question).
3. The acceleration is constant at 12m/s2 (Correct).
4. The particle will never go in the negative direction from its starting point (Correct).
Final Answers:
- The correct options are:
- 1st option: Correct (9 meters at t=2 seconds).
- 2nd option: Incorrect (acceleration is 12m/s2).
- 3rd option: Correct (acceleration is 12m/s2).
- 4th option: Correct (particle never goes negative).
The velocity of the particle is given by the equation:
v=√x
We know that velocity v can also be expressed as:
v=dxdt
Thus, we can equate the two expressions:
dxdt=√x
Rearranging the equation gives:
dx=√xdt
To facilitate integration, we can express this as:
dx√x=dt
Now, we will integrate both sides:
- The left side will be integrated from the initial position x=4 to x.
- The right side will be integrated from t=0 to t.
∫x4dx√x=∫t0dt
- The left side:
2√x∣∣∣x4=2√x−4
- The right side:
t−0=t
2√x−4=t
Rearranging the equation:
2√x=t+4
√x=t+42
Squaring both sides yields:
x=(t+42)2
Now, we can substitute t=2 seconds into the equation:
x=(2+42)2=(62)2=32=9meters
To find the acceleration, we first need to find the velocity as a function of time:
From the expression for x:
x=(t+42)2
Differentiating x with respect to t:
v=dxdt=ddt(t+42)2=12⋅2(t+42)⋅12=t+42
a=dvdt=12
1. At t=2 seconds, the position x=9 meters (Correct).
2. The acceleration a=12m/s2 (Incorrect statement in the question).
3. The acceleration is constant at 12m/s2 (Correct).
4. The particle will never go in the negative direction from its starting point (Correct).
- The correct options are:
- 1st option: Correct (9 meters at t=2 seconds).
- 2nd option: Incorrect (acceleration is 12m/s2).
- 3rd option: Correct (acceleration is 12m/s2).
- 4th option: Correct (particle never goes negative).
Topper's Solved these Questions
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-03
Explore 6 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:Assertion-Reason
Explore 20 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-01
Explore 55 Videos
- ERROR AND MEASUREMENTBook:ALLENChapter:ERROR AND MEASUREMENTExercise:Part-2(Exercise-2)(B)
Explore 22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
Similar Questions
Knowledge Check
The potential energy function for a particle executing linear SHM is given by V(x)=12kx2 where k is the force constant of the oscillator. For k=0.5Nm−1, the graph of V(x) versus x is shown in the figure A particle of total energy E turns back when it reaches x=±xm.if V and K indicate the potential energy and kinetic energy respectively of the particle at x=+xm,then which of the following is correct?
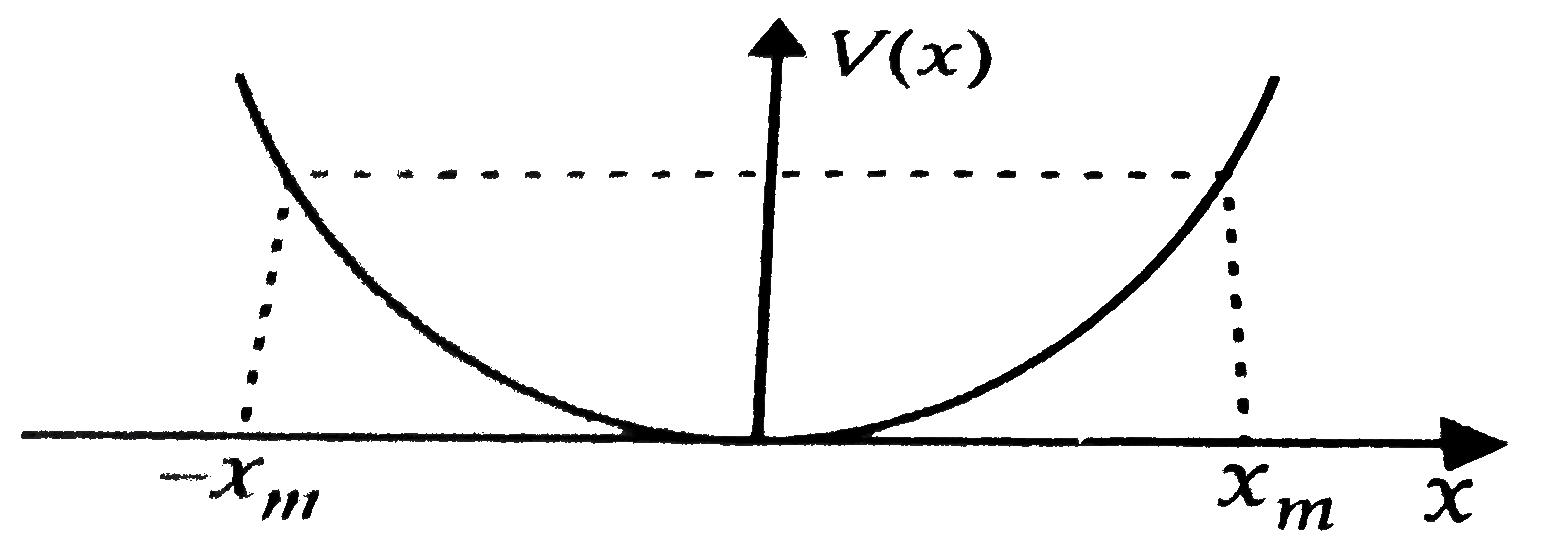 AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
AV=0, K=EBV=E, K=0CV lt K, K=0DV=0, K lt E
Velocity of a particle is given as v=(2t2−3)m/s. The acceleration of particle at t = 3s will be :
View SolutionThe initial velocity of a particle is u (at t = 0) and the acceleration f is given by f = at. Which of the following relation is valid?
View SolutionA particle of mass m with an initial velocity uˆi+2uˆj collides with a particle of mass 3m at rest. After collision, the two particles stick together and the combined particle moves with a velocity vˆi+v'ˆj. Which of the following is incorrect?
View SolutionThe initial velocity of a particle is x ms−1 (at t=0) and acceleration a is function for time, given by, a= 6t. Which of the following relation is correct for final velocity y after time t?
View SolutionThe initial velocity of a particle is u (at t = 0) and the acceleration f is given by f=αt. Which of the following relation is valid?
View Solution
For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as
v=u+at, (u=initial velocity)
Draw the velocity-time graph of the particle in following situations.
(i) Velocity is decresing with time (i.e., acceleration in negative)
(ii) Initial velocity is negative but acceleration is positive
View SolutionIf velocity of a particle is given by v=(2t+3)m/s. Then average velocity in interval 0≤t≤1 s is :
View Solution

