
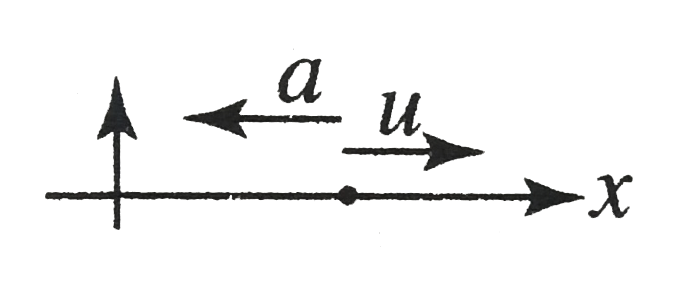
For a particle moving along straight line with constant acceleration (a), we define velocity of the particle with time as
v=u+at, (u=initial velocity)
Draw the velocity-time graph of the particle in following situations.
(i) Velocity is decresing with time (i.e., acceleration in negative)
(ii) Initial velocity is negative but acceleration is positive


We have the relation v=ut+at. If are compare this relation with v=mx+c=c+mx, it is straight line
(i) We have v=u+at.
Compare weith y=c+mx
Have u is positive and a in negative. Hence the straight line should have positive intercept and negative slope.
The graph should be
(ii) Here initial velocity in negative and acceleration is should have positive slope and negative intercept.
Similar Questions
If a particle starts moving with initial velocity u=1ms−1 and acceleration a=2ms−2, the veloctiy of the particle at any time is given by v=u+at=1+2t. Plot the velocity-time graph of the particle.
View SolutionA particle of mass m is moving along the line y-b with constant acceleration a. The areal velocity of the position vector of the particle at time t is (u=0)
View Solution
Knowledge Check
A particle moves in a plane with a constant acceleration in a direction different from the initial velocity. The path of the particle is
Astraight lineBarc of circleCparabolaDellipse
A particle moves in a straight line with a uniform acceleration a. Initial velocity of the particle is zero. Find the average velocity of the particle in first 's' distance.
View SolutionDraw the velocity-time graph of an object moving with uniform negative acceleration.
View SolutionA particle starting from rest moves along a straight line with constant acceleration for this velocity displacement graph will have the form-
View SolutionDraw the velocity-time graph of an object whose speed is increasing at uniform rate but moving with negative acceleration.
View SolutionA particle is moving along x-direction with a constant acceleration a. The particle starts from x=x0 position with initial velocity u. We can define the position of the particle with time by the relation
x=x0+ut+12at2
plot the position of the particle in relation with time is following situations
(i) If initial position of the particle is on negativ x-axis, initial velocity is positive and acceleration is negative.
(ii) If initial position is positive, initial velocity is negative and acceleration is positive.
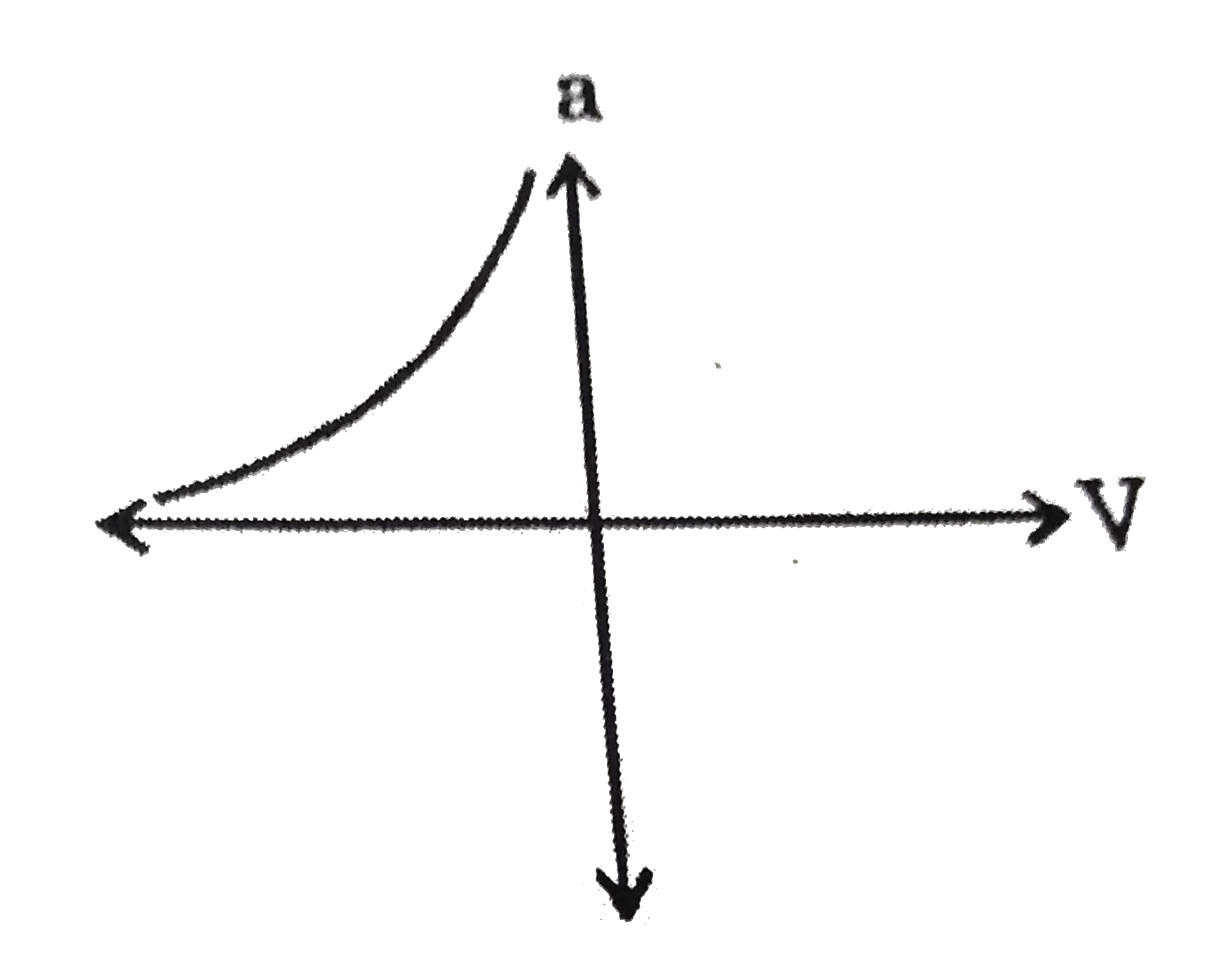
View SolutionA particle moves in straight line. Acceleration of particle changes with velocity as showns in graph:
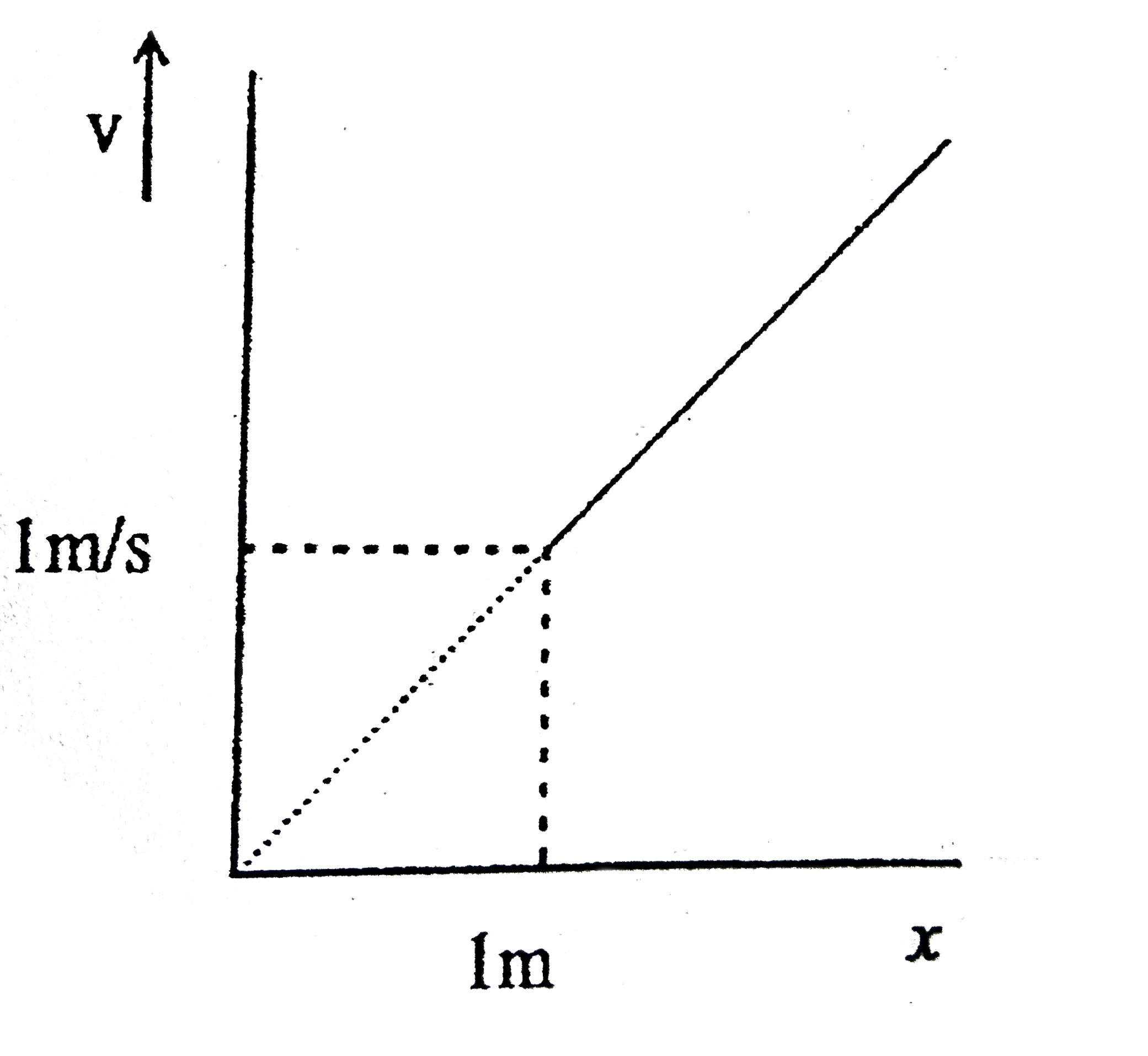
View SolutionA particle is moving in a straight line according to graph given below : (a is acceleration, v is velocity, x is position, t is time) :
View Solution