If the instanetaneous velocity of a particle projected as shown in figure is given by v=aˆi+(b−ct)ˆj where a,b, and c are positive constants, the range on the horizontal plane will be
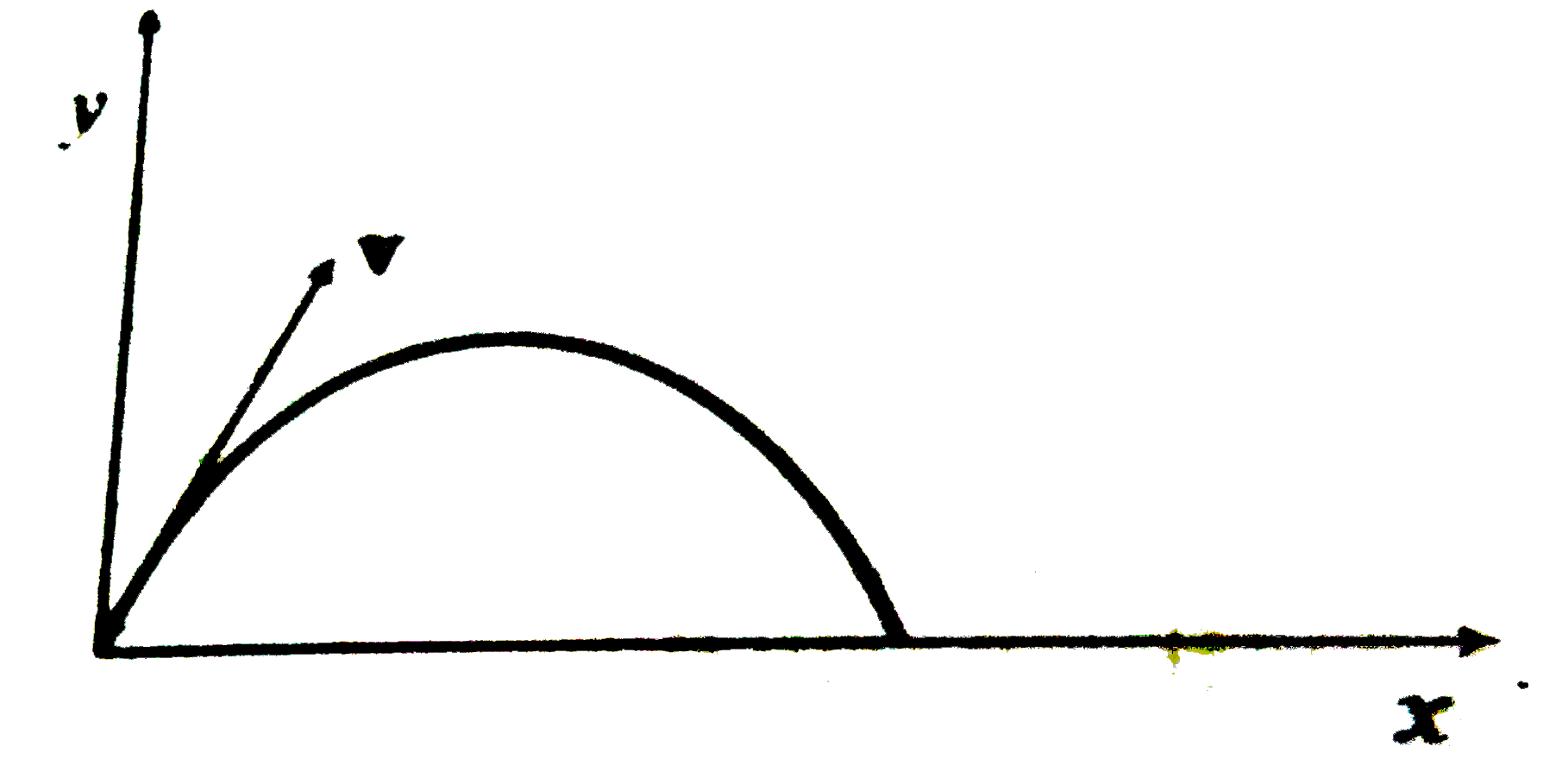
bac
2bac
3bac
None
The correct Answer is:B
→v=aˆi+(b−ct)ˆj
Time to reach maximum height (when ˆj comp. of velocity becomes zero)
∴B−ct=0⇒t=bc∴ Time of fight =2bc
range= horizontal velocity × Time of flight =a×2bc
Topper's Solved these Questions
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-02
Explore 57 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-03
Explore 6 Videos
- KINEMATICSBook:ALLENChapter:KINEMATICSExercise:EXERCISE-2
Explore 89 Videos
- ERROR AND MEASUREMENTBook:ALLENChapter:ERROR AND MEASUREMENTExercise:Part-2(Exercise-2)(B)
Explore 22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
Similar Questions
The linear momentum of a particle as a fuction of time 't' is given by , p = a +bt , where a and b are positive constants . What is the force acting on the particle ?
View SolutionThe velocity vector at a point A varies with time as →v=aˆi+btˆj , where a and b are positive constants. The equation of trajectory of the point would be
View SolutionThe velocity varies with time as →v=aˆi+btˆj , where a and b are positive constants. The magnitude of instantaneous velocity and acceleration would be
View SolutionThe position of a particle as a function of time t, is given by x(t)=at+bt2−ct3 where a,b and c are constants. When the particle attains zero acceleration, then its velocity will be :
View SolutionThe velocity v of a particle at time t is given by v=at+bt+c, where a, b and c are constants. The dimensions of a, b, c are respectively :-
View SolutionThe displacement x of a particle varies with time t as x=ae−αt+beβt. Where a,b,α and β positive constant.
The velocity of the particle will.
View SolutionThe displacement x of a particle varies with time t as x=ae−αt+beβt. Where a,b,α and β positive constant.
The velocity of the particle will.
View SolutionThe coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then
View SolutionThe coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then
View SolutionA particle is projected form a horizontal plane (x−z plane) such that its velocity vector at time t is gives by →V=aˆi+(b−ct)ˆj. Its range on the horizontal plane is given by
View Solution
