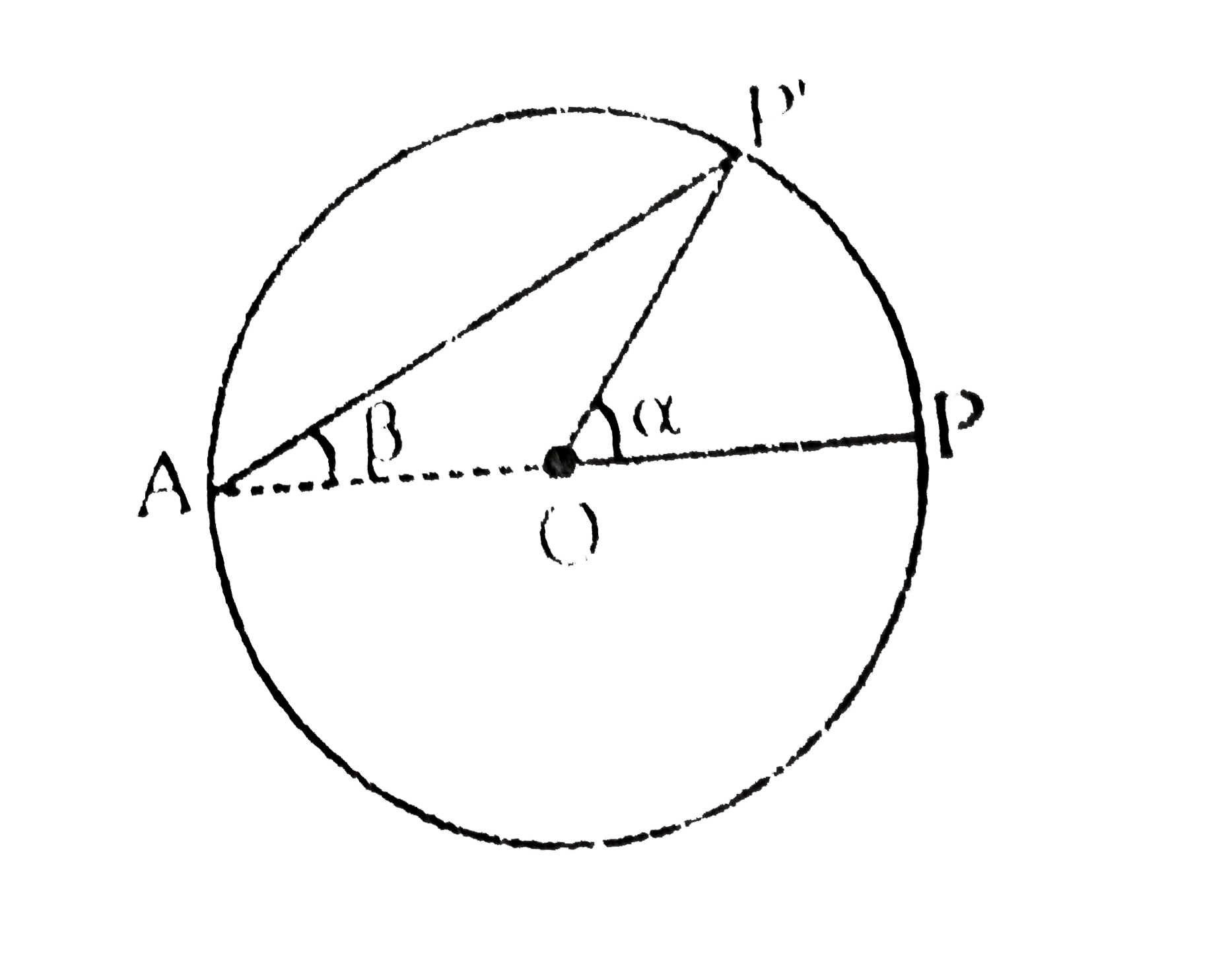
Angular velocity of a particle is given w.r.t. the point which the position vector of particle is considered.
Here ωPO=dαdt
ωPA=dβdt
Prove that ωPO=2ωPA
Step by step video, text & image solution for Angular velocity of a particle is given w.r.t. the point which the position vector of particle is considered. Here omega_(PO)=(dalpha)/(dt) omega_(PA)=(dbeta)/(dt) Prove that omega_(PO)=2omega_(PA) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-01
55 Videos
- KINEMATICSBOOK - ALLENCHAPTER - KINEMATICSEXERCISE - EXERCISE-02
57 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
The angular velocity of a particle is given by ω=1.5t−3t∘+2, Find the time when its angular acceleration becomes zero.
View SolutionThe angular velocity of a particle is →w=4ˆi+ˆj−2ˆk about the origin. If the position vector of the particle is 2ˆi+3ˆj−3ˆk, then its linear velocity is
View SolutionThe position vector of a particle is r=asinωtˆi+acosωtˆj
The velocity of the particle is
View SolutionThe displacement of a particle along the x- axis it given by x=asin2ωt The motion of the particle corresponds to
View SolutionFor a particle of a rotating rigid body, v=rω, which of the following are correct ?
View SolutionThe displacement of a particle along the x-axis is given by x=asin2ωt. The motion of the particle corresponds to
View SolutionA particle, with restoring force proportional to displacement and resulting force proportional to velocity is subjected to a force Fsinωt. If the amplitude of the particle is maximum for ω=ω1, and the energy of the particle is maximum for ω=ω2, then
View SolutionA particle, with restoring force proportional to displacement and resulting force proportional to velocity is subjected to a force Fsinωt. If the amplitude of the particle is maximum for ω=ω1, and the energy of the particle is maximum for ω=ω2, then
View SolutionPosition vector of a particle moving in x−y plane at time t is r=a(1−cosωt)ˆi+asinωtˆj. The path of the particle is
View Solutionthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
View Solution
