Find the value of $x_{1}$ , so that $\int_{0}^{x_{1}} y d x = 5$

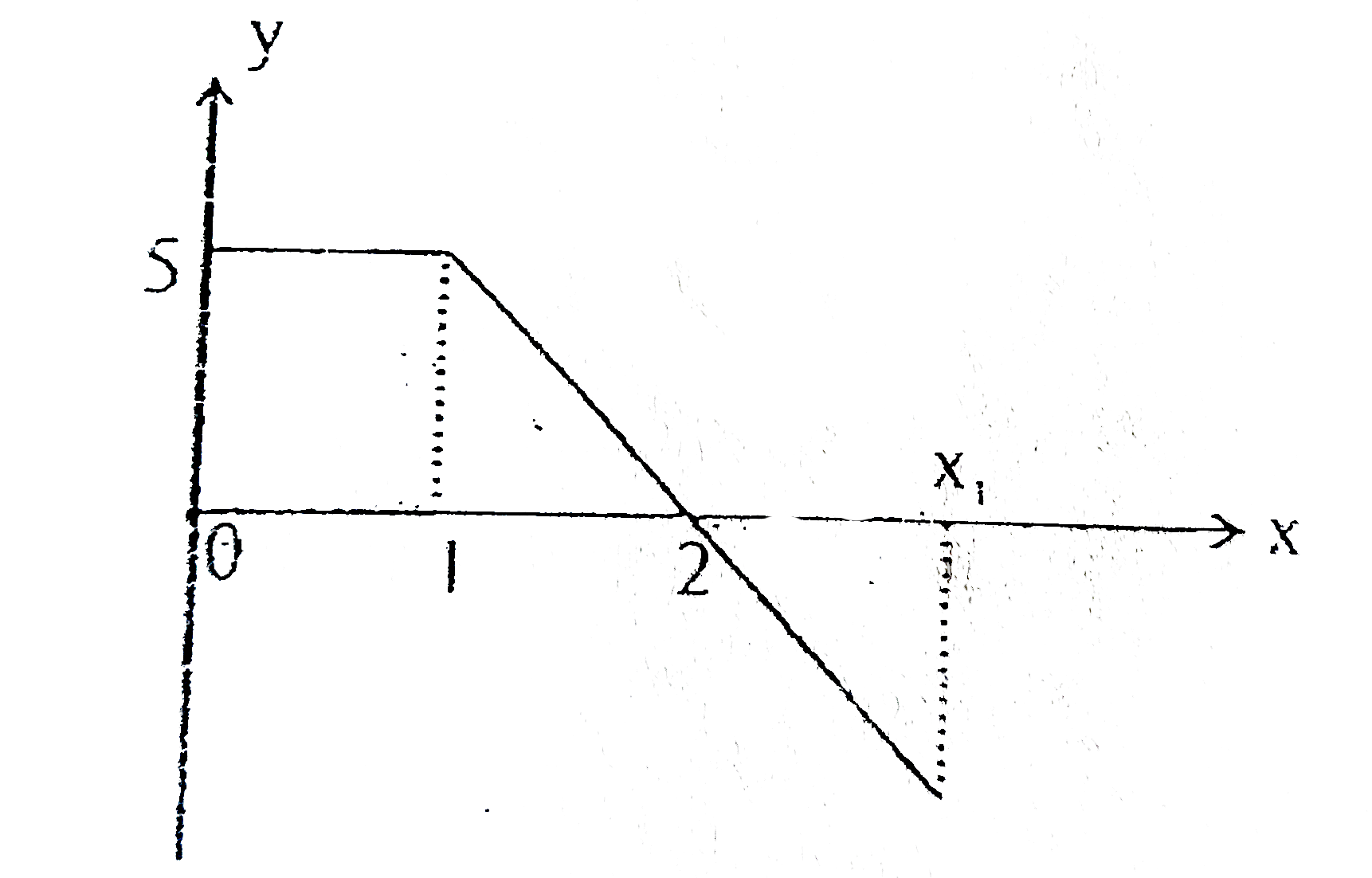
A

$5$

B

$3$

C

$2$

D

$1$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

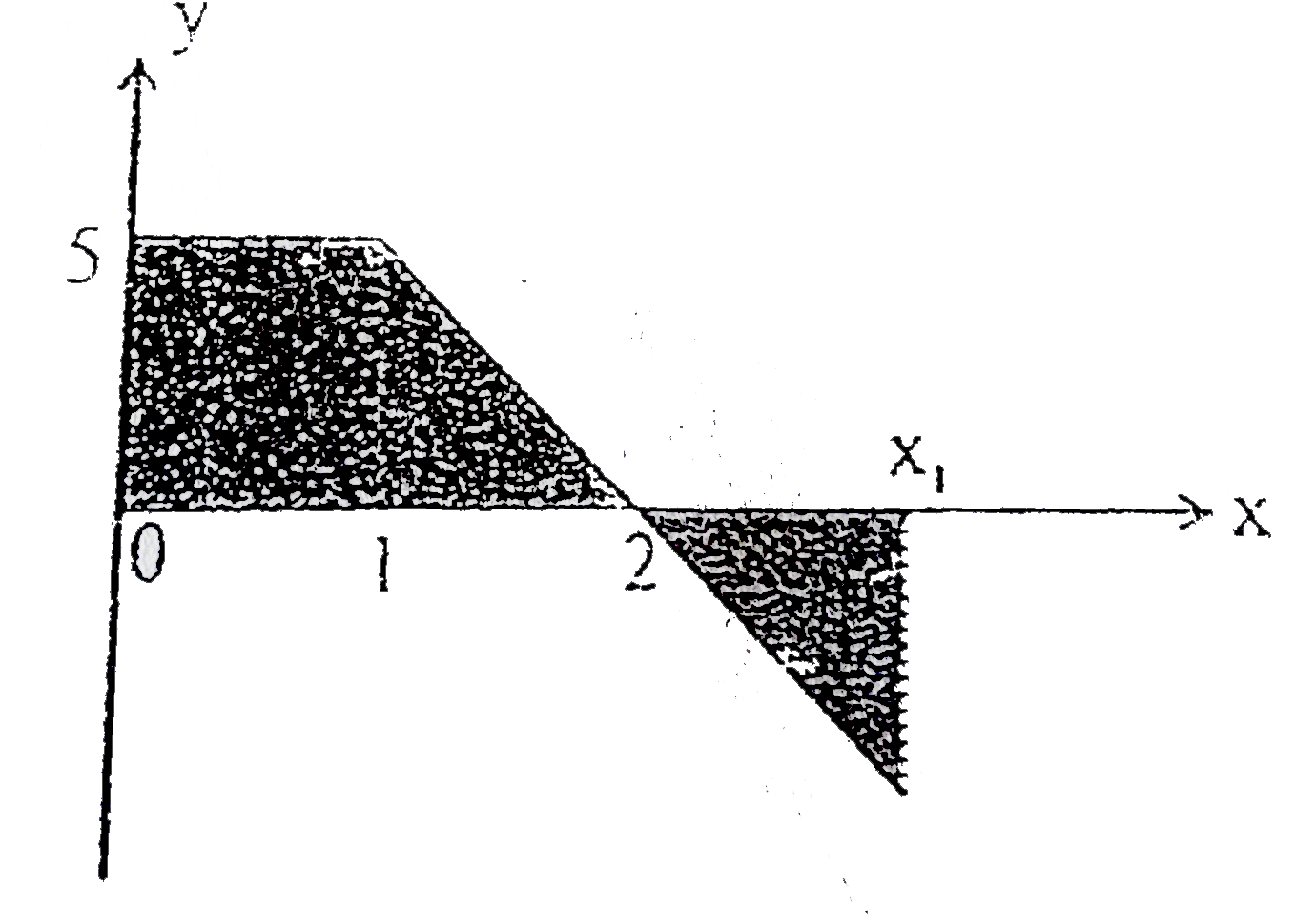
$\int_{0}^{x_{1}} y d x =$ shadded area
$(5 \times 1) + \frac{1}{2} \times (1 + 5) - \frac{1}{2} \times (x_{1} - 2) \times 5 (x_{1} - 2)$
$x_{1} = 3$

Updated on:21/07/2023

|

Class 12 PHYSICS TEST PAPER

Topper's Solved these Questions

Similar Questions

Find the value of $\int_{0}^{1} x (1 - x) d x$
View Solution
If $f (0) = 1, f (2) = 3, f' (2) = 5$ ,then find the value of $I_{1} = \int_{0}^{1} x f'' (2 x) d x$
View Solution
Find the value of $\int_{0}^{1} x {(1 - x)}^{n} d x$
View Solution
The value of the integral $\int_{0}^{1} x {(1 - x)}^{n} d x$ is -
View Solution
Find the value of k, so that the function $f (x) = {\begin{matrix} k x^{2} + 5 & if x \leq 1 2 & if x > 1 \end{matrix}$ is continuous at $x = 1$
View Solution
Find the value of $k$ , so that the function $f (x) = {\begin{matrix} k x^{2} + 5 & if x \leq 1 2 & if x > 1 \end{matrix}$ is continuous at $x = 1$
View Solution
(1) Evaluate $\int_{0}^{1} x^{7} \cdot d x$
View Solution
Find the value of the following: $\int_{0}^{1} \frac{d x}{1 + x^{2}}$
View Solution
Find the value of $\int_{0}^{2 π} \frac{1}{1 + {tan}^{4} x} d x$
View Solution
(i) If $f (x) = \int_{0}^{{sin}^{2} x} {sin}^{- 1} \sqrt{t} d t + \int_{0}^{{cos}^{2} x} {cos}^{- 1} \sqrt{t}$ dt, then prove that $f' (x) = 0 \forall x \in R$ .
(ii) Find the value of x for which function $f (x) = \int_{- 1}^{x} t (e^{t} - 1) (t - 1) {(t - 2)}^{3} {(t - 3)}^{5} d t$ has a local minimum.
View Solution

ALLEN-TEST PAPER-Exercise (Physics)

Home
Ask Doubt
Profile