For conservative force field, $\to F = - \frac{\partial U}{\partial x} ˆ i - \frac{\partial U}{d y} ˆ j - \frac{\partial U}{\partial z} ˆ k$ where $F \to$ Maginitude of Force. $U \to$ Potential energy and $\frac{\partial U}{\partial x} =$ Differentiation of $U$ w.r.t. $x$ keeping $y$ and $z$ constant and so on.

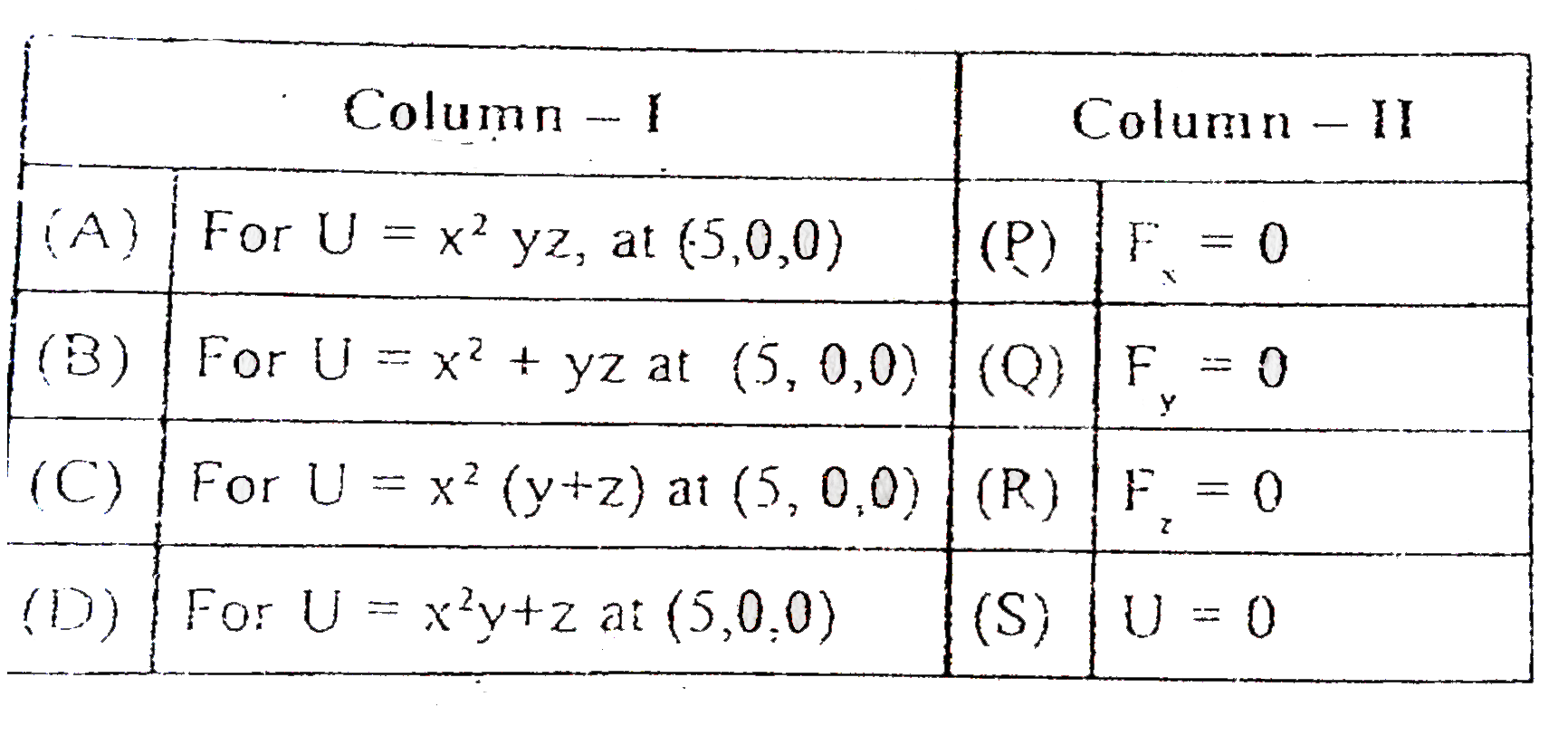
Choose incorrect matching $: -$

A

$(A) \to (P, Q, R, S)$

B

$(B) \to (Q, R)$

C

$(C) \to (P, S)$

D

$(D) \to (P, R, S)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:D

For $(A)$ $:$ $\to F = - 2 x y z ˆ i - x^{2} z ˆ j - x^{2} y ˆ k \Rightarrow F_{x} = 0$ ,
$F_{y} = 0, F_{z} = 0, U = 0$
For $(B)$ : $\to F = - 2 x ˆ i - z ˆ j - y ˆ k \Rightarrow F_{x} \neq 0, F_{y} = 0, F_{z} = 0, U \neq 0$
For $(C)$ $:$ $\to F = - 2 x (y + z) ˆ i - x^{2} ˆ j - x^{2} ˆ k \Rightarrow F_{x} = 0, F_{y} \neq 0, F_{z} \neq 0, U = 0$
For $(D)$ $:$ $\to F = - 2 x y ˆ i - x^{2} ˆ j - ˆ k \Rightarrow F_{x} = 0, F_{y} \neq 0, F_{z} \neq 0, U = 0$

Updated on:21/07/2023

|

Class 12 PHYSICS TEST PAPER

Topper's Solved these Questions

Similar Questions

ALLEN-TEST PAPER-Exercise (Physics)

Home
Ask Doubt
Profile