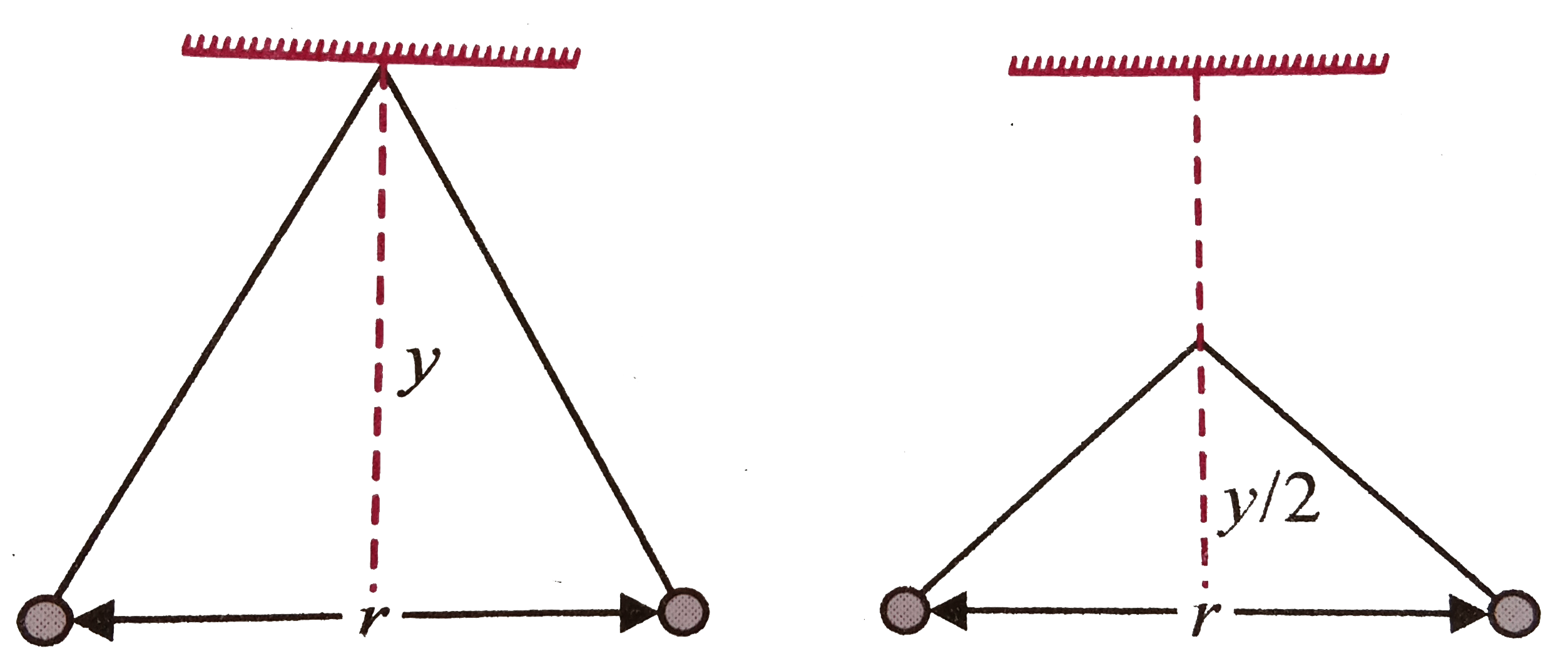
Two identical charged spheres suspended from a common point by two massless strings of length l are initially a distance d(d<<l) apart because of their mutual repulsion. The charge begins to leak from both the spheres at a constant rate. As a result the charges approach each other with a velocity v. then, as a function of distance x between them
v∝x1/2
v∝x
v∝x−1/2
v∝x−1
The correct Answer is:C
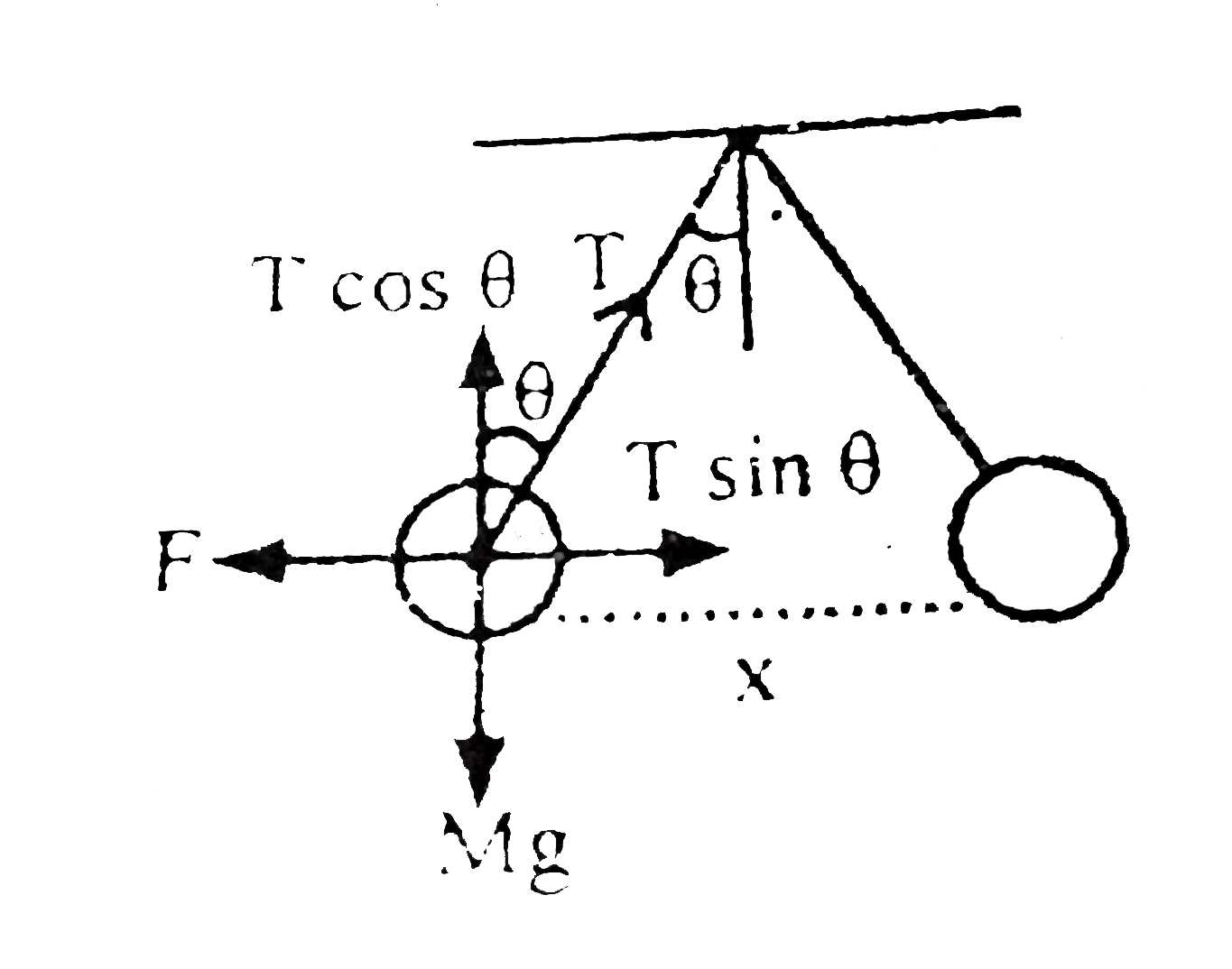
tanθ=FMg (since θ small)
θ=FMg⇒F=Mgθ
KQ2x2=Mgxl
Q2=MgKlx3⇒Q=√MgKlx3/2
(dQdt)=√Mgkl(32x1/2)(dxdt)= constant
so dxdt∝x−1/2 or V∝x−1/2⇒v∝x−1/2
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-05(B)
19 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - MCQ s WITH ONE OR MORE THAN ONE CORRECT ANSWER
6 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice-04[B]
16 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
Two identical charged spheres suspended from a common point by two mass-less strings of length l are initially at a distance d ( d<<l) apart because of their mutual repulsion . The charge begins to leak from both the spheres at a constant rate. As a result the charge approach each other with a velocity v. Then as a function of distance x between them .
View SolutionTwo identical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo indentical pith balls, each carrying charge q, are suspended from a common point by two strings of equal length l. Find the mass of each ball if the angle between the strings is 2θ in equilibrium.
View SolutionTwo path balls carrying equal charges are suspended from a common point by strings of equal length, the strings are rightly clamped at half the height. The equilibrium separation between the balls, now becomes :
View SolutionTwo small spheres, each having a mass of 20 g, are suspended form a common point by two insulating strings of length 40 cm each. The spheres are identically charged and the speration between the balls at equilibrium is found to be 4 cm . Find the charge on each sphere.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo identical balls each having a density ρ are suspended from as common point by two insulating strings of equal length. Both the balls have equal mass and charge. In equilibrium each string makes an angle θ with vertical. Now, both the balls are immersed in a liquid. As a result the angle θ does not change. The density of the liquid is σ. Find the dielectric constant of the liquid.
View SolutionTwo positively charged sphere of masses m1 and m2 are suspended from a common point at the ceiling by identical insulating massless strings of length l. Charges on the two spheres are q1 and q2 respectively. Equilibrium both strings make the same angle θ with the vertical. then
View SolutionTwo identical charged spheres of material density ρ, suspended from the same point by inextensible strings of equal length make an angle θ between the string. When suspended in a liquid of density σ the angle θ remains the same. The dielectric constant K of the liquid is
View SolutionThree paricles, each of mass m and carrying a charge q each, are suspended from a common pointby insulating massless strings each of length L. If the particles are in equilibrium and are located at the corners of an equilateral triangle of side a, calculate the charge q on each particle. Assume L>>a.
View Solution
