Show that, for a given dipole, V & E cannot have the same magnitude at distance less than 2m from the dipole. Suppose that the distance is √5m, determine the directions along which V & E are equal in magnitude.
The correct Answer is:45∘,135∘,225∘,315∘
To solve the problem, we will break it down into two parts as outlined in the question.
Part 1: Show that V and E cannot have the same magnitude at a distance less than 2m from the dipole.
1. Understanding the formulas:
- The electric potential V due to a dipole is given by:
V=kpcosθr2
- The electric field E due to a dipole is given by:
E=kp√1+3cos2θr3
2. Setting the magnitudes equal:
- We want to find when |V|=|E|:
kpcosθr2=kp√1+3cos2θr3
3. Canceling common terms:
- Cancel kp from both sides (assuming kp≠0):
cosθr2=√1+3cos2θr3
4. Rearranging the equation:
- Multiply both sides by r3:
rcosθ=√1+3cos2θ
5. Squaring both sides:
- To eliminate the square root, square both sides:
r2cos2θ=1+3cos2θ
6. Rearranging the equation:
- Rearranging gives:
r2cos2θ−3cos2θ=1
cos2θ(r2−3)=1
7. Finding the condition for r:
- This implies:
cos2θ=1r2−3
- For cos2θ to be valid, r2−3 must be positive, which means:
r2>3⇒r>√3≈1.732
- Therefore, the minimum distance r must be at least 2 meters.
Conclusion for Part 1:
Thus, we have shown that for a given dipole, V and E cannot have the same magnitude at a distance less than 2 meters from the dipole.
---
Part 2: Determine the directions along which V and E are equal in magnitude at r=√5 m.
1. Using the derived equation:
- We will use the equation:
cos2θ=1r2−3
- Substitute r=√5:
cos2θ=1(√5)2−3=15−3=12
2. Finding cosθ:
- Taking the square root gives:
cosθ=±1√2=±√22
3. Finding the angles:
- The angles corresponding to cosθ=√22 are:
θ=π4andθ=7π4
Conclusion for Part 2:
Thus, the directions along which the magnitudes of V and E are equal at a distance of √5 meters are θ=π4 and θ=7π4.
---
- The electric potential V due to a dipole is given by:
V=kpcosθr2
- The electric field E due to a dipole is given by:
E=kp√1+3cos2θr3
- We want to find when |V|=|E|:
kpcosθr2=kp√1+3cos2θr3
- Cancel kp from both sides (assuming kp≠0):
cosθr2=√1+3cos2θr3
- Multiply both sides by r3:
rcosθ=√1+3cos2θ
- To eliminate the square root, square both sides:
r2cos2θ=1+3cos2θ
- Rearranging gives:
r2cos2θ−3cos2θ=1
cos2θ(r2−3)=1
- This implies:
cos2θ=1r2−3
- For cos2θ to be valid, r2−3 must be positive, which means:
r2>3⇒r>√3≈1.732
- Therefore, the minimum distance r must be at least 2 meters.
Thus, we have shown that for a given dipole, V and E cannot have the same magnitude at a distance less than 2 meters from the dipole.
- We will use the equation:
cos2θ=1r2−3
- Substitute r=√5:
cos2θ=1(√5)2−3=15−3=12
- Taking the square root gives:
cosθ=±1√2=±√22
- The angles corresponding to cosθ=√22 are:
θ=π4andθ=7π4
Thus, the directions along which the magnitudes of V and E are equal at a distance of √5 meters are θ=π4 and θ=7π4.
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exersice-04[B]
Explore 16 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-05(A)
Explore 35 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Comprehension 9
Explore 2 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
Describe the locus of point at distances less than or equal to 2.5 cm from a given point.
View SolutionA short electric dipole is situated at the origin of coordinate axis with its axis along x-axis and equator along y-axis. It is found that the magnitudes of the electric intensity and electric potential due to the dipole are equal at a point distance r=√5m from origin. Find the position vector of the point in first quadrant.
View Solution
Knowledge Check
In a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges are placed at (n−1) corners. At the centre, the intensity is E and the potential is V. The ratio V/E has magnitude
ArnBr(n−1)C(n−1)/rDr(n−1)/n
If the force exerted by an electric dipole on a charge q at distance of 1 m is F, the force at a point 2 m away in the same direction will be
View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign saperated by a distance 2 a as shown in figure . The dipole is along the x axis and is centered at the origin
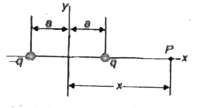
(A) Calculate the electric potential at point P .
(B ) Calculate V at a point far from the dipole .
View SolutionAn electric dipole consists of two charges of equal magnitude and opposite sign separately by a distance 2a. The dipole is along the X-axis and is centred at the origin
(i) Calculate the electric potential at point P
(ii) Calculate V at a point far from the dipole.
View SolutionAn electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field, the force on it and its potential energy are respectively
View SolutionAn electric dipole is formed by +4μC and −4μCcharges at 5 m m distance. Calculate the dipole moment and give its direction.
View SolutionIn a regular polygon of n sides, each corner is at a distance r from the centre. Identical charges are placed at (n−1) corners. At the centre, the intensity is E and the potential is V. The ratio V/E has magnitude
View SolutionAn electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field, the force on it and its potential energy are respectively
(a) 2qE and minimum (b) qE and pE
(c) zero and minimum (d) qE and maximum
View Solution