An electric dipole is formed by +4μC and −4μCcharges at 5 m m distance. Calculate the dipole moment and give its direction.
To solve the problem of calculating the dipole moment of an electric dipole formed by charges of +4 µC and -4 µC separated by a distance of 5 mm, we can follow these steps:
Step 1: Understand the formula for dipole moment
The dipole moment (P) is given by the formula:
P=q⋅d
where:
- q is the magnitude of one of the charges,
- d is the separation distance between the charges.
Step 2: Convert the given values to SI units
- The charge q=4μC=4×10−6C
- The separation distance d=5mm=5×10−3m
Step 3: Calculate the dipole moment
Substituting the values into the formula:
P=(4×10−6C)⋅(5×10−3m)
Step 4: Perform the multiplication
Calculating the numerical part:
P=4×5×10−6×10−3
P=20×10−9C⋅m
P=2.0×10−8C⋅m
Step 5: Determine the direction of the dipole moment
The direction of the dipole moment is defined as pointing from the negative charge to the positive charge. Therefore, in this case, the direction is from -4 µC to +4 µC.
Final Answer
The dipole moment is 2.0×10−8C⋅m and its direction is from -4 µC to +4 µC.
---
The dipole moment (P) is given by the formula:
P=q⋅d
where:
- q is the magnitude of one of the charges,
- d is the separation distance between the charges.
- The charge q=4μC=4×10−6C
- The separation distance d=5mm=5×10−3m
Substituting the values into the formula:
P=(4×10−6C)⋅(5×10−3m)
Calculating the numerical part:
P=4×5×10−6×10−3
P=20×10−9C⋅m
P=2.0×10−8C⋅m
The direction of the dipole moment is defined as pointing from the negative charge to the positive charge. Therefore, in this case, the direction is from -4 µC to +4 µC.
The dipole moment is 2.0×10−8C⋅m and its direction is from -4 µC to +4 µC.
Topper's Solved these Questions
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:TRY YOURSELF
Explore 33 Videos
- ELECTRIC CHARGES AND FIELDS Book:AAKASH INSTITUTE ENGLISHChapter:ELECTRIC CHARGES AND FIELDS Exercise:ASSIGNMENT(SECTION-A) Objective Type Question
Explore 45 Videos
- DUAL NATURE OF RADIATION AND MATTER Book:AAKASH INSTITUTE ENGLISHChapter:DUAL NATURE OF RADIATION AND MATTER Exercise:ASSIGNMENT (SECTION-D)
Explore 10 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
Explore 15 Videos
Similar Questions
4 charges are placed each at a distance a from origin . The dipole moment of configuration is .
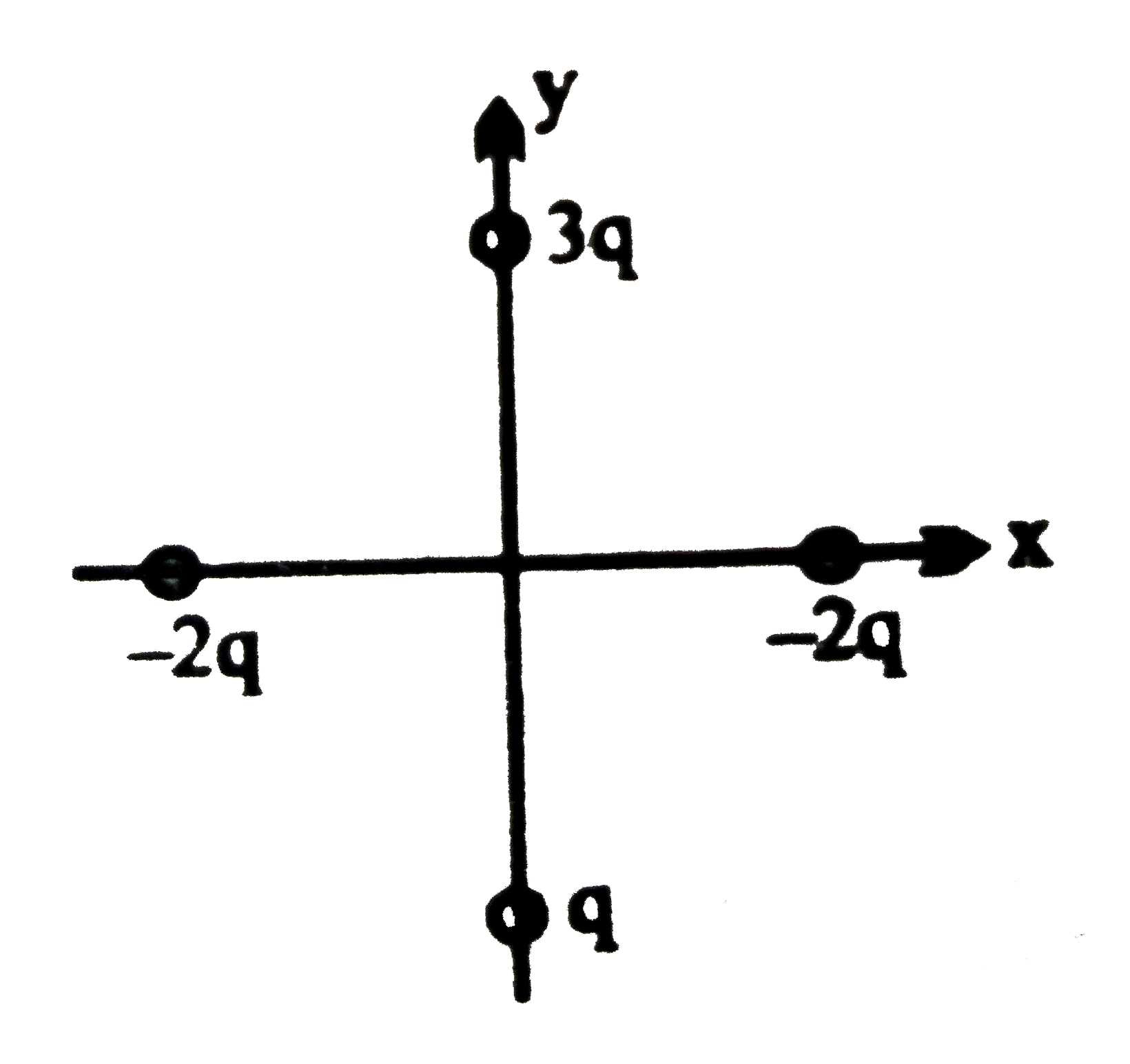 .
.
View SolutionAn electric dipole is kept on the axis of a uniformly charged ring at distance from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is p, charge of the ring is Q & radius of the ring is R. The force on the dipole is
View SolutionCharges ±20nC are separated by 5mm. Calculate the magnitude and direction of dipole moment.
View SolutionAn electric dipole consists of two opposite charges each of magnitude 2 μC separated by a distance 1 cm. The dipole is placed in an external field of 103 N/C. The maximum torque on the dipole is
View SolutionAn electric dipole consists of two opposite charges of magnitude 1μC separated by a distance of 2cm.The dipole is placed in an electric filled 10−5Vm−1.The maximum torque that the field exert on the dipole is
View SolutionA small electric dipole is kept on the axis of a uniformly charged ring at distance R/√2 from the centre of the ring. The direction of the dipole moment is along the axis. The dipole moment is P, charge of the ring is Q and radius of the ring is R. The force on the dipole is nearly _____
View SolutionTwo point charges 4μCand−2μC are separated by a distance of 1m in air. Calculate at what point on the line joining the two charges is the electric potential zero ?
View SolutionAn electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field, the force on it and its potential energy are respectively
View SolutionAn electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field, the force on it and its potential energy are respectively
(a) 2qE and minimum (b) qE and pE
(c) zero and minimum (d) qE and maximum
View Solution
Two point electric dipoles with dipole moment P1 and P2 are separated by a distance r with their dipole axes mutually perpendicular as shown. The force of interaction between the dipoles is (where k=14πε0)
View Solution