An infinite, uniformly charged sheet with surface charge density cuts through a spherical Gaussian surface of radius R at a distance x from its center, as shown in the figure. The electric flux through the Gaussian surface is :

The correct Answer is:D
∵ Electric field
=σ∈0 due to infinitely uniform charged.
Electric flux
=Σenclosed∈0=∫σ∈0×[πR2−πx2]
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-03
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-04
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)
19 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
An infinite, uniformly charged sheet with surface charge density σ cuts through a spherical Gaussian surface of radius R at a distance X from its center, as shown in the figure. The electric flux Φ through the Gaussian surface is .

View SolutionThe electric flux through the surface

View SolutionThe electric flux through the surface

View SolutionThe electric flux through the surface

View SolutionFind out flux through the given Gaussian surface.

View SolutionWhich of the following is true for electric-flux through a Gaussian surface ?
View SolutionA hemispherical surface of radius R is kept in a uniform electric field E as shown in figure. The flux through the curved surface is

View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.

View SolutionA non - conducting disc of radius R is uniformly charged with surface charge density σ. A disc of radius R2 is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be

View SolutionRefer to the arrangement of charges in Fig and a Gaussian surface of radius R with Q at the centre. Then
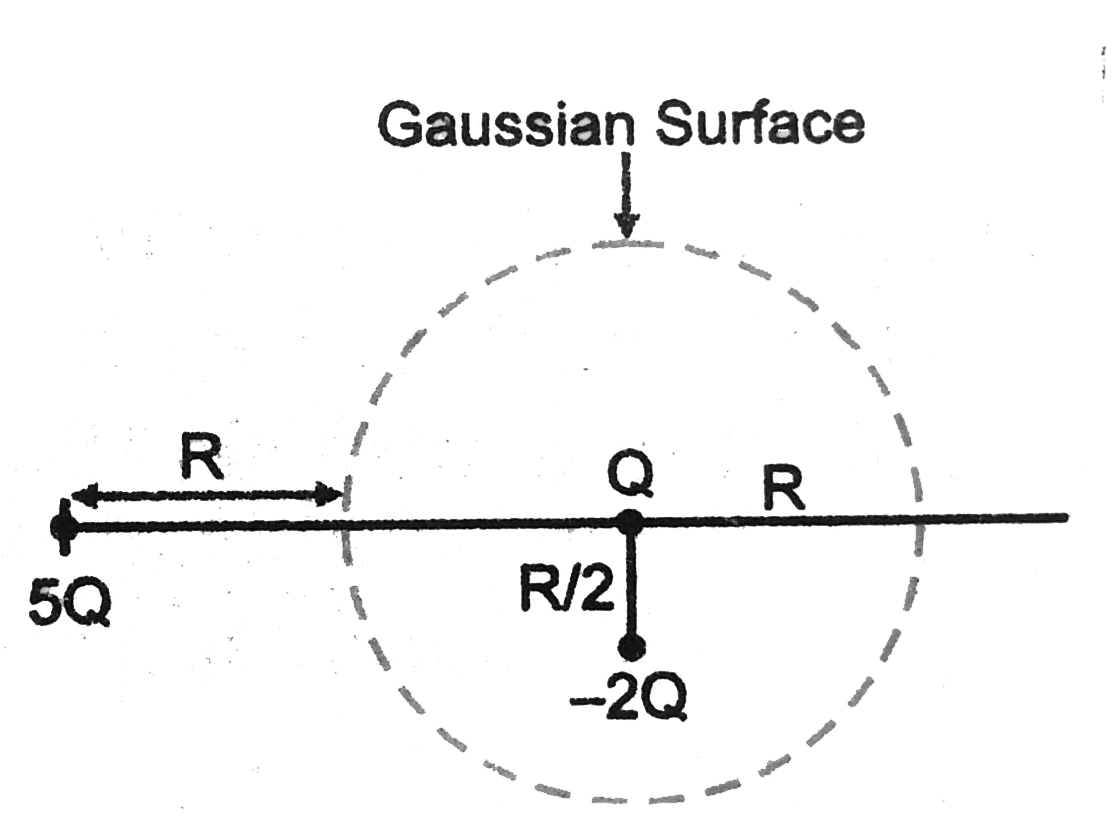
View Solution
