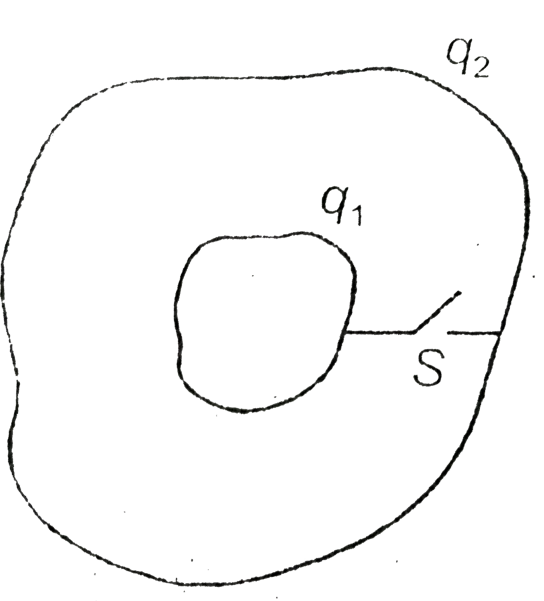
Charges Q1 and Q2 lie inside and outside respectively of a closed surface S. Let E be the field at any point S and ϕ be the flux of E over S.
The correct Answer is:A, B, C
Electric flux depends on the total charge enclosed by the closed surface S. Hence flux is related with charge Q1. Electric field at a point is the vector sum of the all electric field intensities due to all charges.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-03
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-04
1 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exersice -05(B)
19 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
Charges Q1andQ2 lie inside and outside, respectively, of a closed surface S. Let E be the field at any point on S and ϕ be the flux of E over S.
View SolutionCharges Q1andQ2 lie inside and outside, respectively, of a closed surface S. Let E be the field at any point on S and ϕ be the flux of E over S.
View SolutionIf charge q1 and q2 lies inside and outside respectively of a closed surface S. Let E be the electric field at any point on S and ϕ be the electric flux over S. Select the incorrect option.
View SolutionTwo conducting closed surfaced shells are shown in figure. They are connected by wire through switch S. If q1 and q2 charges are given to inner and outer shells respectively . The switch is closed find the ratio of final charge to initial charge for each shell.
View SolutionLet E1 and E2, be two ellipses whose centers are at the origin.The major axes of E1 and E2, lie along the x-axis and the y-axis, respectively. Let S be the circle x2+(y−1)2=2. The straight line x+ y =3 touches the curves S, E1 and E2 at P,Q and R, respectively. Suppose that PQ=PR=2√23.If e1 and e2 are the eccentricities of E1 and E2, respectively, then the correct expression(s) is(are):
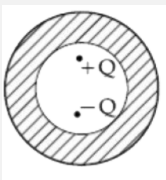
View SolutionShow in the figure are two point charge + Q and - Q inside the cavity of the Spherical .shell the changes are kept near the surface of the cavity on opposite sides of the centre of the shell if σ1 is the surface charge on the inner surface and Q1 net charge on it and σ2 the surface charge on the outer surface and Q2 net charge on it then :
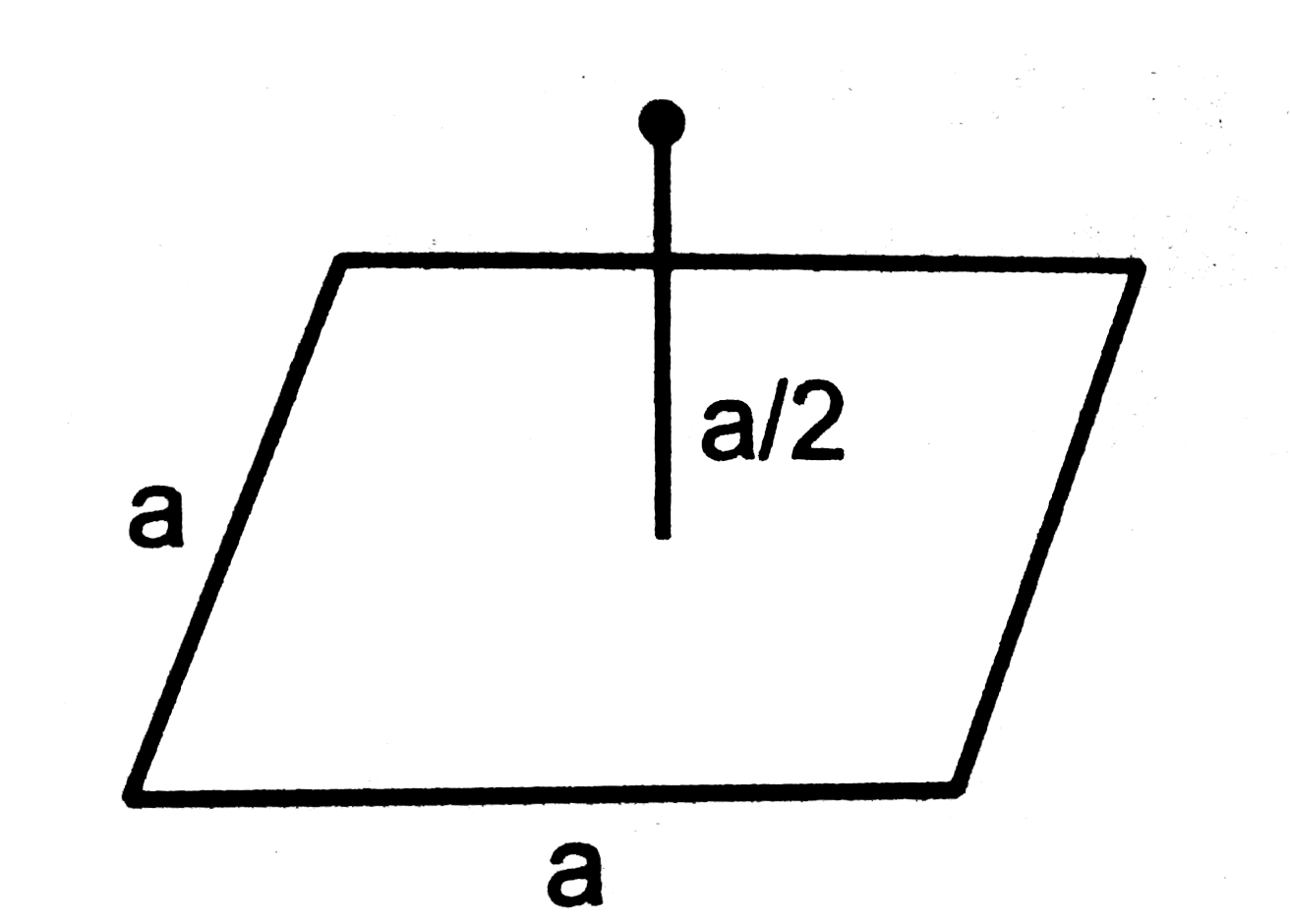
View SolutionA charge Q is placed at a distance a2 above the centre of a horizontal, spuare surface of edge a as shown in figure (30-E1). Find the flux of the electric field through the square surface.
View SolutionIf an isolated infinite plate contains a charge Q1 on one of its surfaces and a charge Q2 on its other surface, then prove that electric field intensity at a point in front of the plate will be Q/2Aε0, where Q=Q1+Q2
View SolutionIn figure (a), a charge q is placed just outside the centre of a closed hemisphere. In figure (b), the same charge q is placed just inside the centre of the closed hemisphere and in figure (c), the charge is placed at the centre of hemisphere open from the base. Find the electric flux passing through the hemisphere in all the three cases.

View SolutionAs shown in Figure, charge Q is kept in the inner cavity and a charge of 2Q and 3Q are imparted to the inner and outermost shells.
(a) Find charge at each of the surface .
(b) Find E in the first annular region and outside.
View Solution
