In a certain system of absolute units the acceleration produced by gravity in a body falling freely is denoted by 3, the kinetic energy of a 272.1kg shot moving with velocity 448 metres per second is denoted by 100, and its momentum by 10.
The unit of length is
15.36 m
153.6 m
68.57 m
None of these
The correct Answer is:B
To solve the problem step by step, we will analyze the given information and derive the unit of length in the specified system of absolute units.
Step 1: Understanding the Given Information
We have three pieces of information:
1. The acceleration due to gravity is denoted by 3.
2. The kinetic energy of a 272.1kg shot moving with a velocity of 448ms is denoted by 100.
3. The momentum of the shot is denoted by 10.
Step 2: Define the Units
Let:
- \( L_1 \) = unit of length in the new system
- \( m_1 \) = unit of mass in the new system
- \( t_1 \) = unit of time in the new system
Step 3: Write the Equations Based on Given Information
Equation 1: Acceleration
The acceleration \( a \) is given by:
\(
a = \frac{L_1}{t_1^2}
\)
In the new system, this is denoted by 3, so we have:
\(
\frac{L_1}{t_1^2} = 3 \quad \text{(1)}
\)
Equation 2: Kinetic Energy
The kinetic energy \( KE \) is given by:
\(
KE = \frac{1}{2} m v^2
\)
Substituting the values:
\(
KE = \frac{1}{2} \times 272.1 \times (448)^2
\)
The unit of kinetic energy is \( m_1 L_1^2 t_1^{-2} \). In the new system, this is denoted by 100, so we have:
\(
\frac{1}{2} \times 272.1 \times (448)^2 = 100 \quad \text{(2)}
\)
Equation 3: Momentum
The momentum \( p \) is given by:
\(
p = m v
\)
Substituting the values:
\(
p = 272.1 \times 448
\)
The unit of momentum is \( m_1 L_1 t_1^{-1} \). In the new system, this is denoted by 10, so we have:
\(
272.1 \times 448 = 10 \quad \text{(3)}
\)
Step 4: Solve the Equations
From Equation 1:
Rearranging gives:
\(
L_1 = 3 t_1^2 \quad \text{(4)}
\)
From Equation 2:
Calculating the left side:
\(
KE = \frac{1}{2} \times 272.1 \times 448^2 = 272.1 \times 100224 \approx 136,00000
\)
Setting this equal to 100:
\(
13600000 = 100 m_1 L_1^2 t_1^{-2} \quad \text{(5)}
\)
From Equation 3:
Calculating the left side:
\(
p = 272.1 \times 448 \approx 121,000.8
\)
Setting this equal to 10:
\(
121000.8 = 10 m_1 L_1 t_1^{-1} \quad \text{(6)}
\)
Step 5: Substitute and Solve for \( L_1 \)
From equations (5) and (6), we can express \( m_1 \) in terms of \( L_1 \) and \( t_1 \).
Substituting \( L_1 \) from equation (4) into equation (5) and (6) and solving will give us the value of \( L_1 \).
After performing the calculations, we find:
\(
L_1 = 153.6 \text{ meters}
\)
Final Answer
The unit of length \( L_1 \) in the new system is 153.6 meters.
---
We have three pieces of information:
1. The acceleration due to gravity is denoted by 3.
2. The kinetic energy of a 272.1kg shot moving with a velocity of 448ms is denoted by 100.
3. The momentum of the shot is denoted by 10.
Let:
- \( L_1 \) = unit of length in the new system
- \( m_1 \) = unit of mass in the new system
- \( t_1 \) = unit of time in the new system
The acceleration \( a \) is given by:
\(
a = \frac{L_1}{t_1^2}
\)
In the new system, this is denoted by 3, so we have:
\(
\frac{L_1}{t_1^2} = 3 \quad \text{(1)}
\)
The kinetic energy \( KE \) is given by:
\(
KE = \frac{1}{2} m v^2
\)
Substituting the values:
\(
KE = \frac{1}{2} \times 272.1 \times (448)^2
\)
The unit of kinetic energy is \( m_1 L_1^2 t_1^{-2} \). In the new system, this is denoted by 100, so we have:
\(
\frac{1}{2} \times 272.1 \times (448)^2 = 100 \quad \text{(2)}
\)
The momentum \( p \) is given by:
\(
p = m v
\)
Substituting the values:
\(
p = 272.1 \times 448
\)
The unit of momentum is \( m_1 L_1 t_1^{-1} \). In the new system, this is denoted by 10, so we have:
\(
272.1 \times 448 = 10 \quad \text{(3)}
\)
Rearranging gives:
\(
L_1 = 3 t_1^2 \quad \text{(4)}
\)
Calculating the left side:
\(
KE = \frac{1}{2} \times 272.1 \times 448^2 = 272.1 \times 100224 \approx 136,00000
\)
Setting this equal to 100:
\(
13600000 = 100 m_1 L_1^2 t_1^{-2} \quad \text{(5)}
\)
Calculating the left side:
\(
p = 272.1 \times 448 \approx 121,000.8
\)
Setting this equal to 10:
\(
121000.8 = 10 m_1 L_1 t_1^{-1} \quad \text{(6)}
\)
From equations (5) and (6), we can express \( m_1 \) in terms of \( L_1 \) and \( t_1 \).
\(
L_1 = 153.6 \text{ meters}
\)
The unit of length \( L_1 \) in the new system is 153.6 meters.
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:DATA SUFFICIENCY QUESTIONS
Explore 3 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-04 [A]
Explore 28 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Comprehension 3
Explore 5 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
In a certain system of absolute units the acceleration produced by gravity in a body falling freely is denoted by 3, the kinetic energy of a 272.1kg shot moving with velocity 448 metres per second is denoted by 100, and its momentum by 10.
the unit of mass is
View SolutionIn a certain system of absolute units the acceleration produced by gravity in a body falling freely is denoted by 5, the kinetic energy of a 500 kg shot moving with velocity 400 metres per second is denoted by 2000 & its momentum by 100
The unit of mass is :-
View SolutionIn a certain system of absoulte units the acceleration produced by gravity in a body falling freely is denoted by 5, the kinetic energy of a 500 kg shot moving with velocity 400 metres per second is denoted by 2000 & its momentum by 100
The unit of length is :-
View Solutionn a certain system of absoulte units the acceleration produced by gravity in a body falling freely is denoted by 5, the kinetic energy of a 500 kg shot moving with velocity 400 metres per second is denoted by 2000 & its momentum by 100
The unit of time is :-
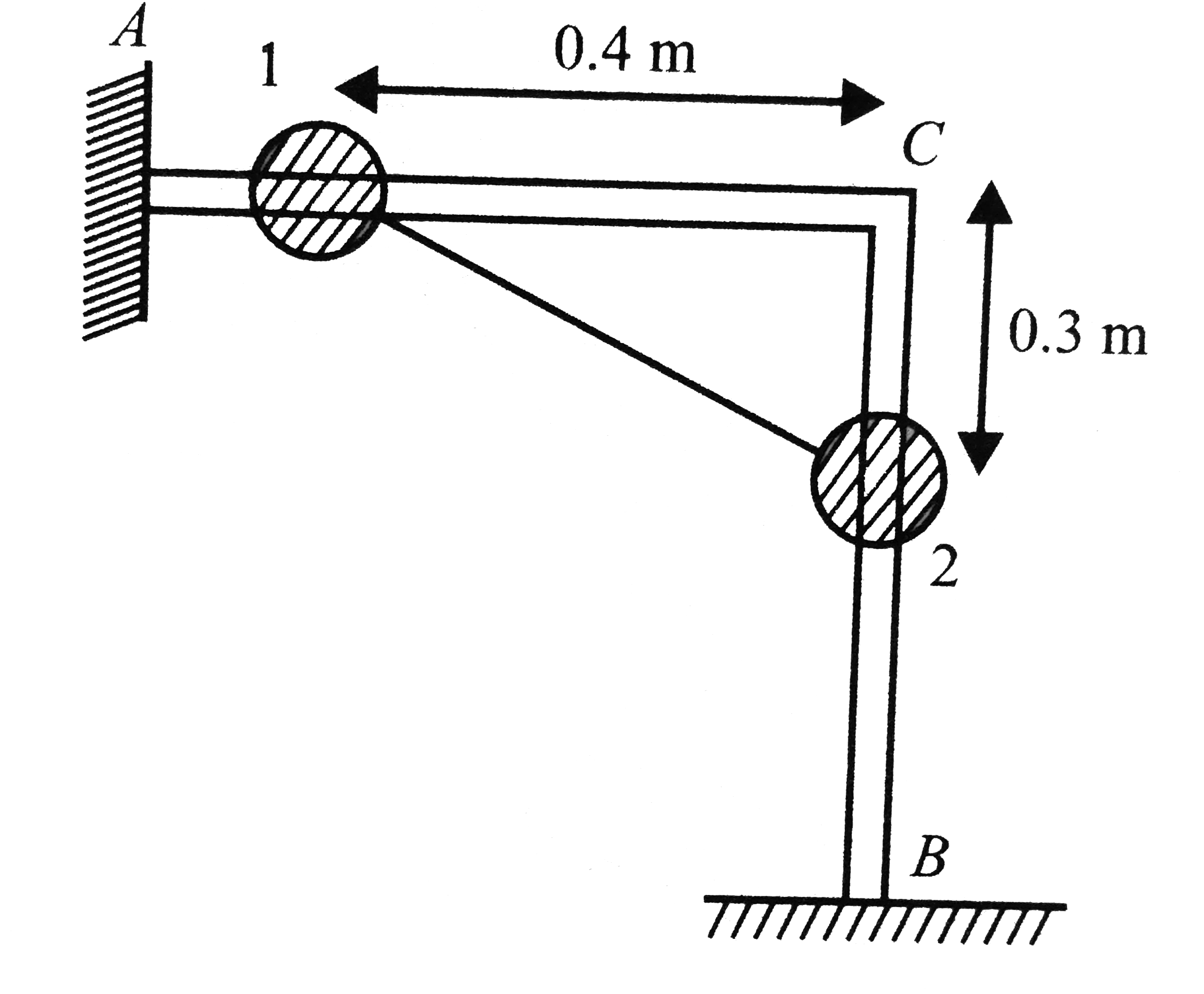
View SolutionTwo identical beads, each of m=100g, are connected by an inextensible massless string, which can slide along the two arms AC and BC of a rigid smooth wire frame in a vertical plane. If the system is released from rest, the kinetic energy of the first bead when the second bead has moved down by a distance of 0.1m is ×x10−3J. Find the value of x(g=10ms−2) (shown situation is after movement of 0.1m).
View Solution1 joule of energy is to be converted into new system of units in which length is measured in 10 metre, mass in 10 kg and time in 1 minute. The numerical value of 1 J in the new system is :-
View SolutionIn ancient time, deffernt system of units was following in which unit of mass was "ser", unit of length was "gaj" & unit of time was "kall" 1ser=900gm, 1gaj=90cm, 1kaal=3hr. A ball of mass 9kg is moving with velocity 10m/s. Then its momentum (mv) in ancient system will be :−
View SolutionThree spheres, each of mass m, can slide freely on a frictionless, horizontal surface. Spheres A and B are attached to an inextensible, inelastic cord of length l and are at rest in the position shown where sphere B is struck by sphere C which is moving to the right with a velocity v0. Knowing that the cord is taut where sphere B is struck by sphere C and assuming 'head on' inelastic impact between B and C, we cannot conserve kinetic energy of the entire system.
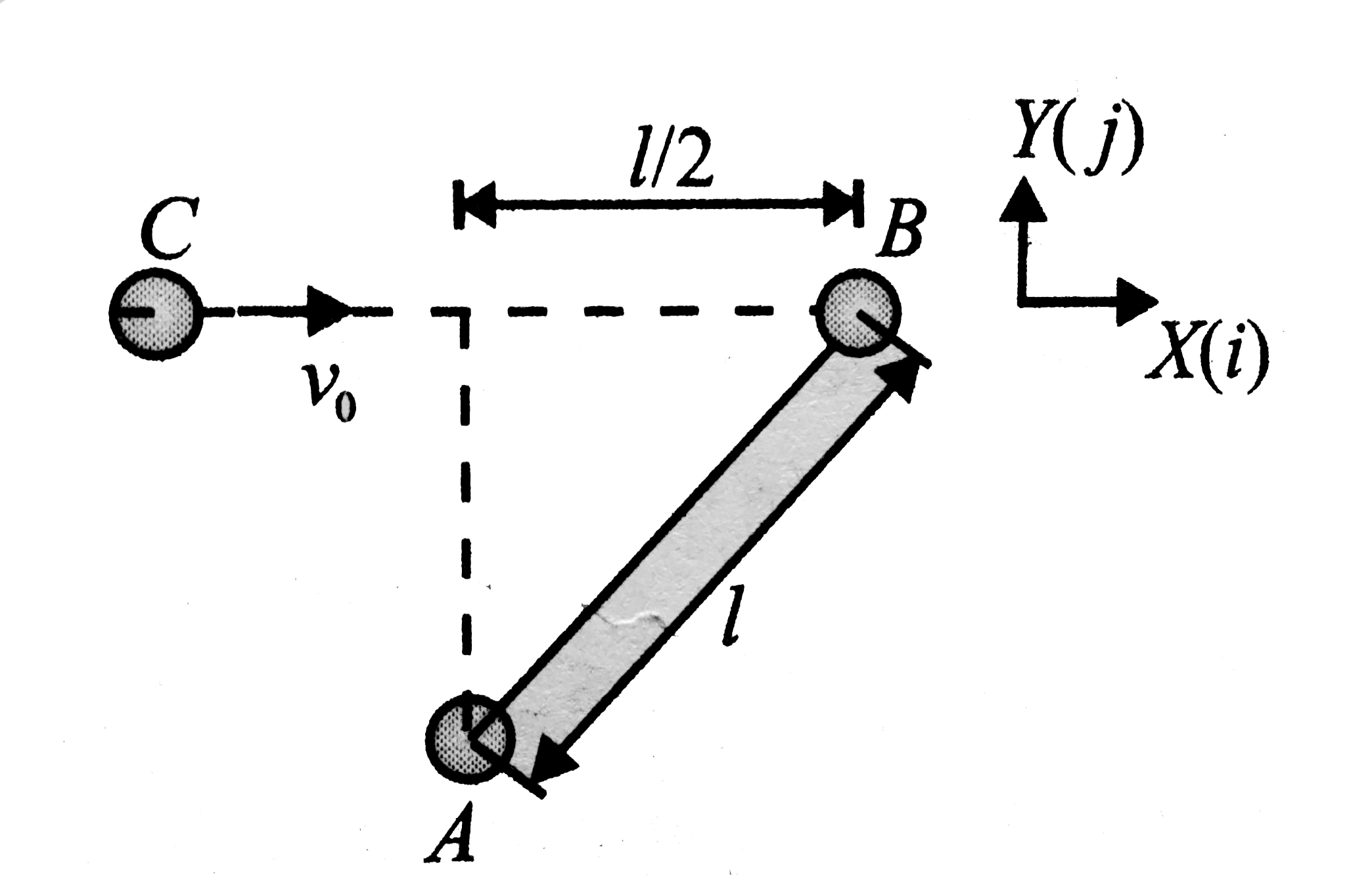 The velocity of B immediately after collision is along unit vector
The velocity of B immediately after collision is along unit vector
View SolutionTwo block A and B of masses m1=3kg and m2=6kg respectively are connected with each other by a spring of force constant k=200N/m as shown in figure. Blocks are pulled away from each other by x0=3cm and then released. When spring is in its natural length and block are moving towards each other, another block C of mass m=3kg moving with velocity v0=0.4m/s (towards right) collides with A and gets stuck to it. Neglecting friction, calculate

(a) velocity v1 and v2 of the blocks A and B respectively just before collision and their angular frequency .
(b) velocity of centre of mass of the system, after collision,
( c) amplitude of oscillation of combined body,
(d) loss of energy during collision.
View SolutionIn a new system of units, unit of mass is taken as 50 kg. unit of length as 100 m and unit of time is 1 minute. What will be the weight of a body in this system, if in SI sysem, its weight is 10 N?
View Solution
