Path traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
In above question initial acceleration (i.e.d2→rdt2) of particle is, if
r
=at
i
^
−bt
2
j
^:-
2bˆj
aˆi
−2bˆj
None of these
The correct Answer is:C
d2→rdt2=−2bˆj
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 4
6 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - DATA SUFFICIENCY QUESTIONS
3 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Comprehension 2
8 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
Path traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
In above the velocity (i.e.d→rdt) at t=0 is, if r =at i ^ −bt 2 j ^ :-
View SolutionPath traced by a moving particle in space is called trajectory of the particle. Shape of trajectiry is decided by the forces acting on the particle. When a coordinate system is associated with a particle motion, the curve equation in which the particle moves [y=f(x)] is called equation of trajectory. It is just giving us the relation among x and y coordinates of the particle i.e. the locus of particle. To find equation of trajectory of a particle, find first x and y coordinates of the particle as a function of time eliminate the time factor.
The position vector of car w.r.t. its starting point is given as →r=atˆi−bt2ˆj where a and b are positive constants. The locus of a particle is:-
View SolutionA particle moves along the curve y=x2+2x. At what point(s) on the curve are the x and y coordinates of the particle changing at the same rate?
View SolutionA particle moves along the curve y=x2+2x. At what point(s) on the curve are the x and y coordinates of the particle changing at the same rate?
View SolutionConsider the motion of a particle described by x=acost,y=asintandz=t . The trajectory traced by the particle as a function of time is
View SolutionThe x and y coordinates of the center of mass of the three-particle system shown below are :
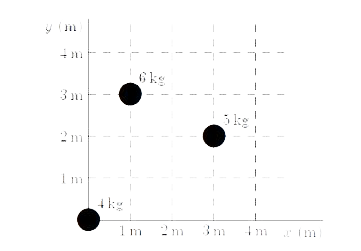
View SolutionThe momentum of a moving particle given by p=tlnt. Net force acting on this particle is defined by equation F=dpdt. The net force acting on the particle is zero at time
View SolutionThe coordinates of a particle moving in x-y plane at any time t are (2t,t2). Find (a) the trajectory of the particle, (b) velocity of particle at time t and (c) acceleration of particle at any time t.
View SolutionA particle moves along the curve y=x2+2x . At what point(s) on the curve are x and y coordinates of the particle changing at the same rate?
View SolutionA particle moves under force F=5(x−2)3 .Motion of the particle is
View Solution
