The energy density u is plotted against the distance r from the centre of a spherical charge distribution on a log-log scale. Find the magnitude of slope of obtained straight line.
The correct Answer is:4
To solve the problem, we need to find the slope of the line when the energy density u is plotted against the distance r from the center of a spherical charge distribution on a log-log scale.
1. Understand the Energy Density Formula:
The energy density u in an electric field is given by:
u=12ϵ0E2
where ϵ0 is the permittivity of free space and E is the electric field.
2. Electric Field for a Spherical Charge Distribution:
For a spherical charge distribution with total charge Q, the electric field E at a distance r from the center (for r greater than the radius of the sphere) is given by:
E=kQr2
where k is Coulomb's constant.
3. Substituting the Electric Field into the Energy Density Formula:
Substitute the expression for E into the energy density formula:
u=12ϵ0(kQr2)2
Simplifying this gives:
u=12ϵ0k2Q2r4
This can be rewritten as:
u=C⋅1r4
where C=12ϵ0k2Q2 is a constant.
4. Taking the Logarithm of Both Sides:
To analyze the relationship on a log-log scale, take the logarithm of both sides:
logu=logC−4logr
5. Identifying the Linear Relationship:
The equation can be rearranged to resemble the linear form y=mx+b:
logu=−4logr+logC
Here, y=logu, x=logr, and the slope m=−4.
6. Finding the Magnitude of the Slope:
The magnitude of the slope is simply the absolute value of −4:
Magnitude of the slope=4
Final Answer:
The magnitude of the slope of the obtained straight line is 4.
The energy density u in an electric field is given by:
u=12ϵ0E2
where ϵ0 is the permittivity of free space and E is the electric field.
For a spherical charge distribution with total charge Q, the electric field E at a distance r from the center (for r greater than the radius of the sphere) is given by:
E=kQr2
where k is Coulomb's constant.
Substitute the expression for E into the energy density formula:
u=12ϵ0(kQr2)2
Simplifying this gives:
u=12ϵ0k2Q2r4
This can be rewritten as:
u=C⋅1r4
where C=12ϵ0k2Q2 is a constant.
To analyze the relationship on a log-log scale, take the logarithm of both sides:
logu=logC−4logr
The equation can be rearranged to resemble the linear form y=mx+b:
logu=−4logr+logC
Here, y=logu, x=logr, and the slope m=−4.
The magnitude of the slope is simply the absolute value of −4:
Magnitude of the slope=4
The magnitude of the slope of the obtained straight line is 4.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Video
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Exercise-01
87 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Question
1 Video
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
_S01_027_Q01.png)
If the law of gravitation be such that the force of attraction between two particles vary inversely as the 5/2th powr of their separation then the graph of orbital velocity v0 plotted against the distance r of a satellite from the earth's centre on a log-log scale is shown alongside the slope oline will be
View SolutionFor spherical charge distribution gives as .
⎧⎨⎩ρ=ρ0(1−r3)whenr≤3mρ=0whenr>3m
( where x is the distance form the centre of spherical charge distribution)
The electric field intensity is maximum for the value of r=_______m.
View Solution
Knowledge Check
The correct plot of the magnitude of magnetic field →B vs distance r from centre of the wire is, if the radius of wire is R
A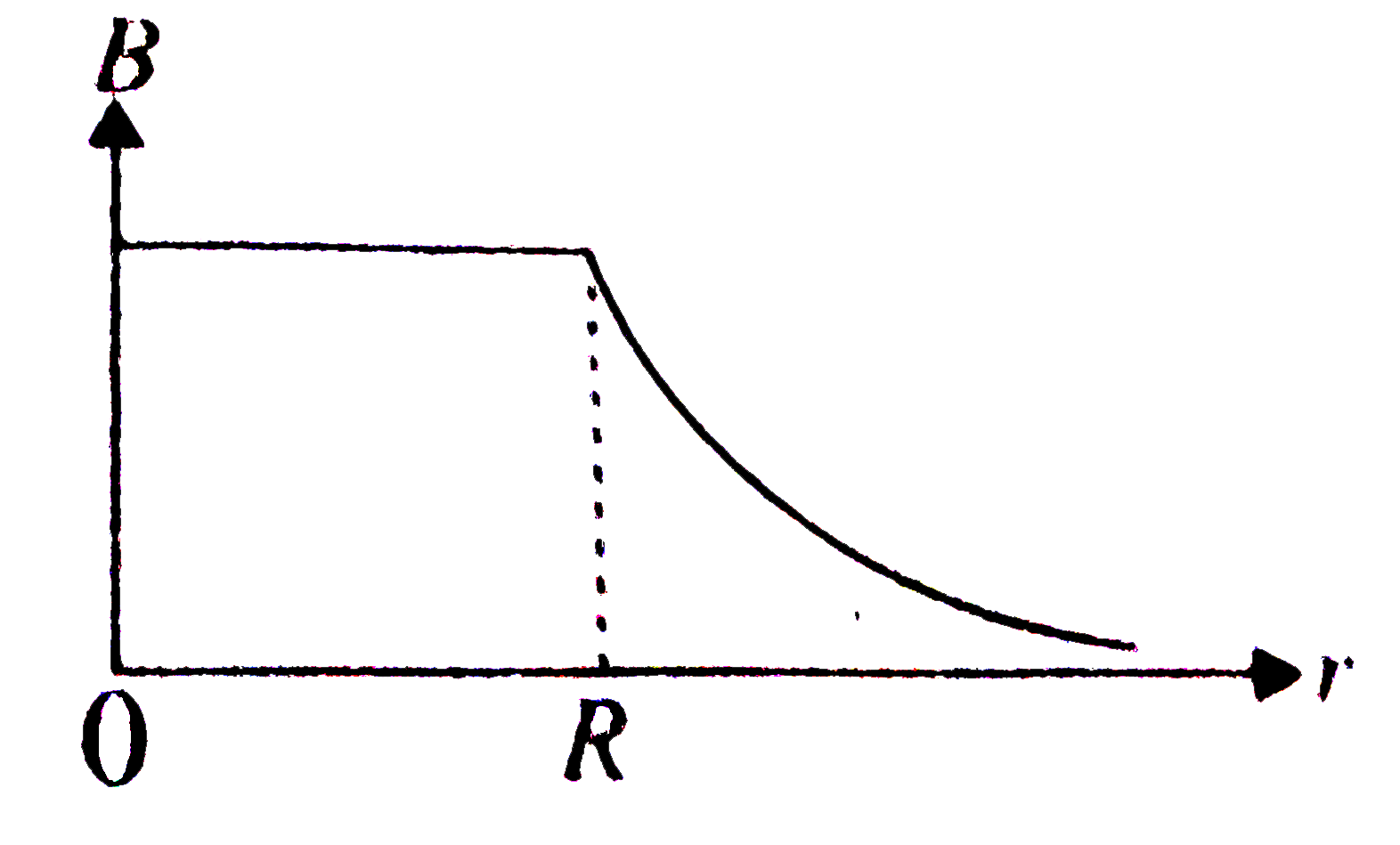 B
B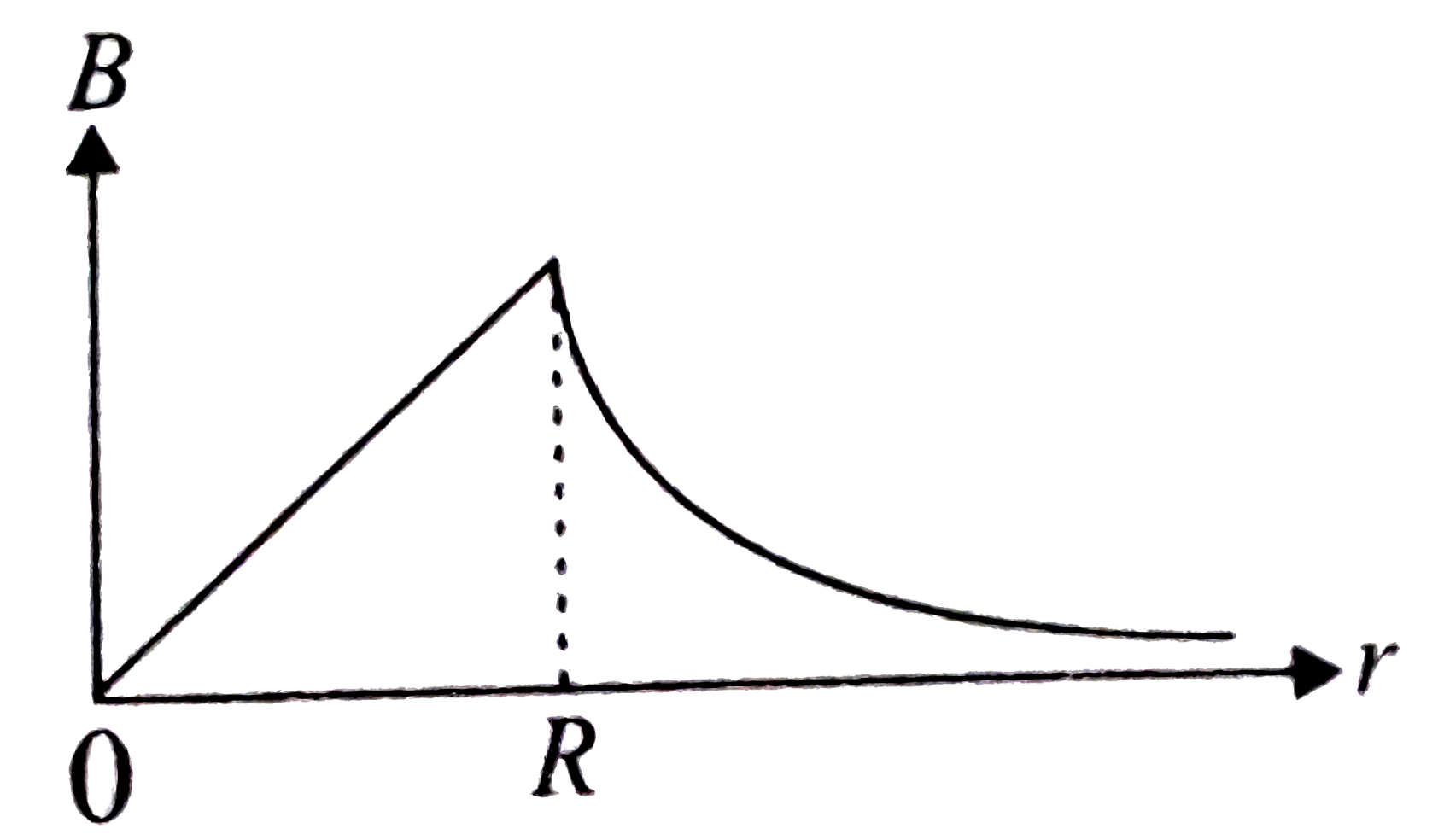 C
C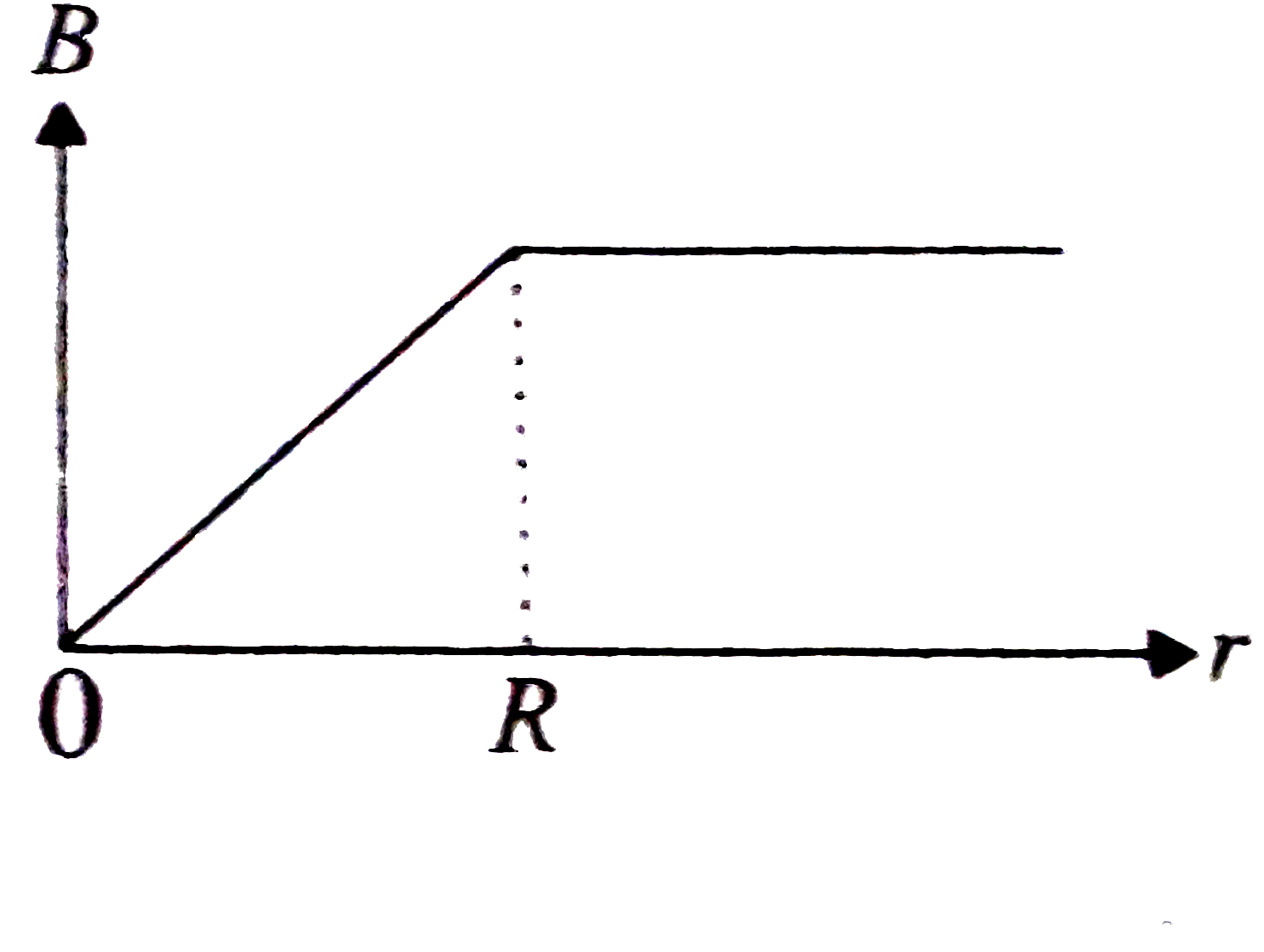 D
D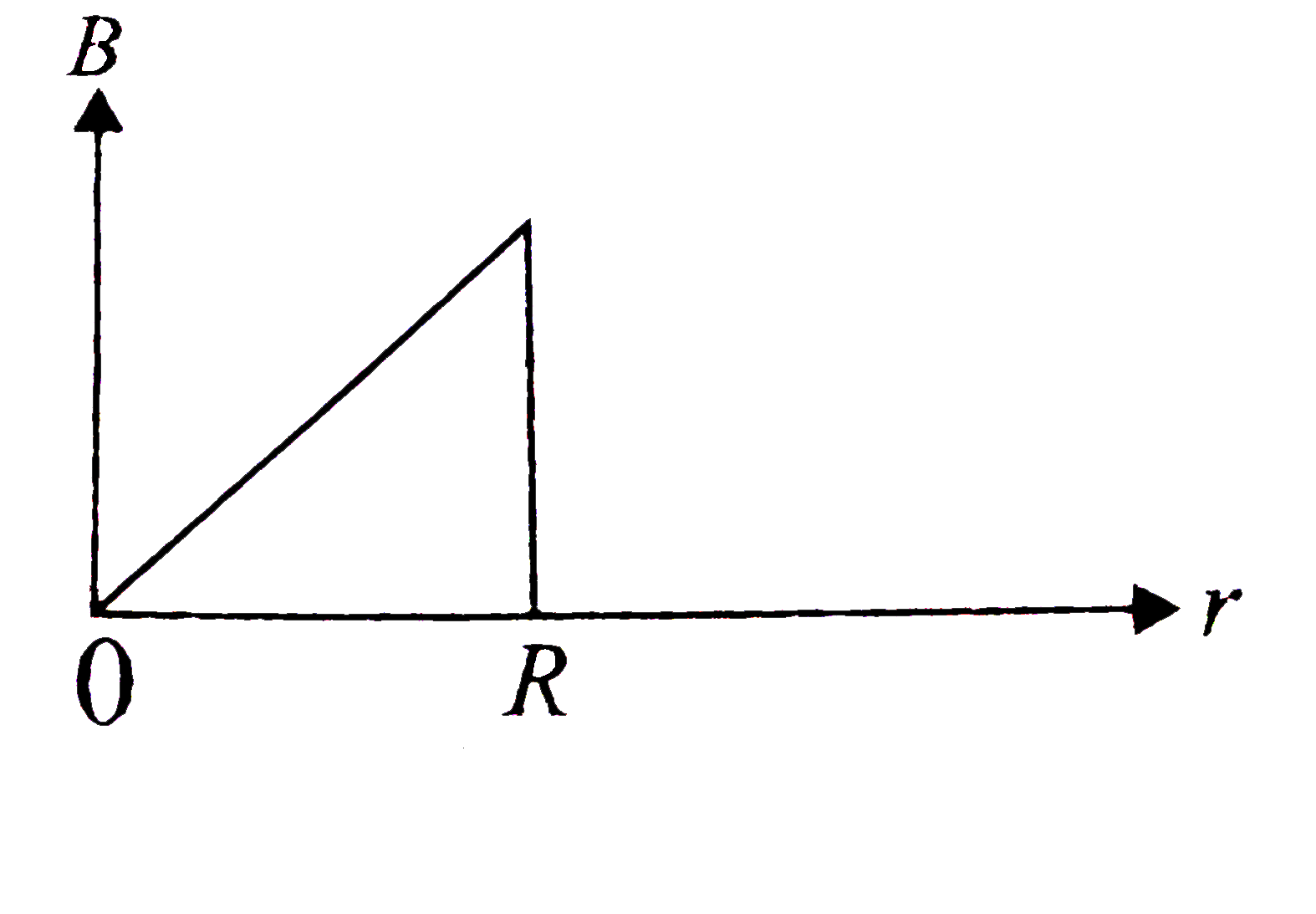
A point charge q is situated at a distance r from one end of a thin conduction rod of length L having a charge Q (uniformly distributed a long its length).find the magnitudes of electric force between the two.
View SolutionA sphere of radius R carries charge such that its volume charge density is proportional to the square of the distance from the centre. What is the ratio of the magnitude of the electric field at a distance 2 R from the centre to the magnitude of the electric field at a distance of R/2 from the centre?
View SolutionIntensity of electric field at a point at a perpendicular distance .r. from an infinite line charge, having linear charge density .λ. is given by :
View SolutionCharge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionA charge q is placed at a distance of 2R from the centre of a spherical conducting shell of radius R. What is electrical potential, due to charges induced on the shell, at a point which is farthest from the point charge ?
View SolutionA point charge q is located at the centre fo a thin ring of radius R with uniformly distributed charge −q, find the magnitude of the electric field strength vectro at the point lying on the axis of the ring at a distance x from its centre, if x>>R.
View SolutionA point charge q is placed at a distance of r from the centre O of an uncharged spherical shell of inner radius R and outer radius 2R. The electric potential at the centre of the shell will be

View Solution

