Calculate the electric field at origin due to infinite number of charges as shown in figure below.
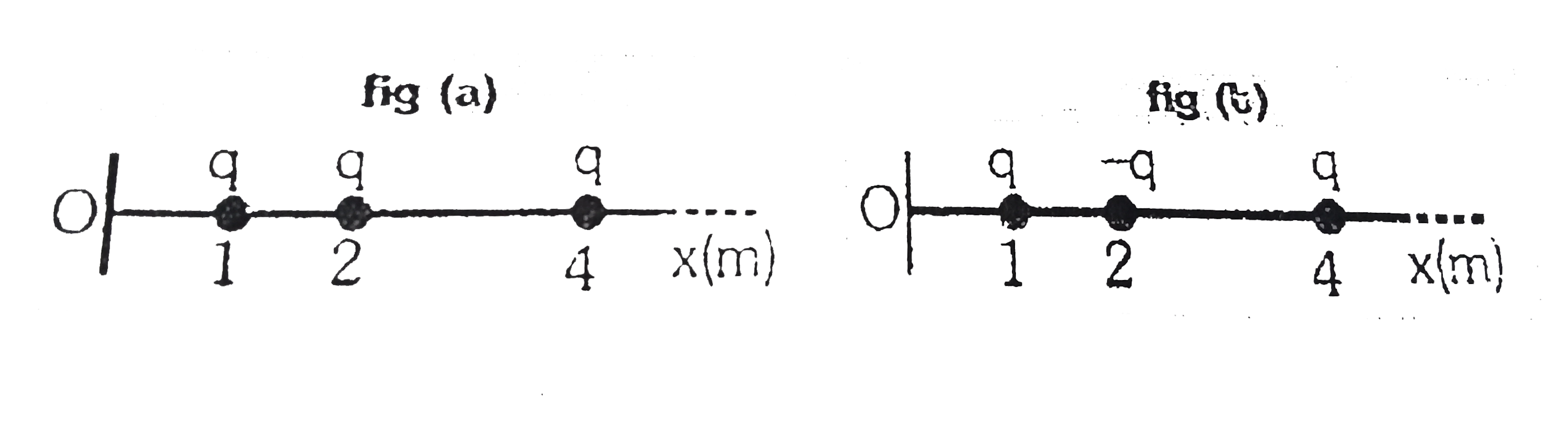
(a)
(b)
Topper's Solved these Questions
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Part -II Example Some worked out Examples
Explore 1 Video
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Exercise-01
Explore 87 Videos
- MISCELLANEOUSBook:ALLENChapter:MISCELLANEOUSExercise:Question
Explore 1 Video
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Book:ALLENChapter:KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)Exercise:BEGINNER S BOX-7
Explore 8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Book:ALLENChapter:PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT Exercise:EXERCISE-IV
Explore 8 Videos
Similar Questions
the electric field at origin due to infinite number of changes as shown in figure is

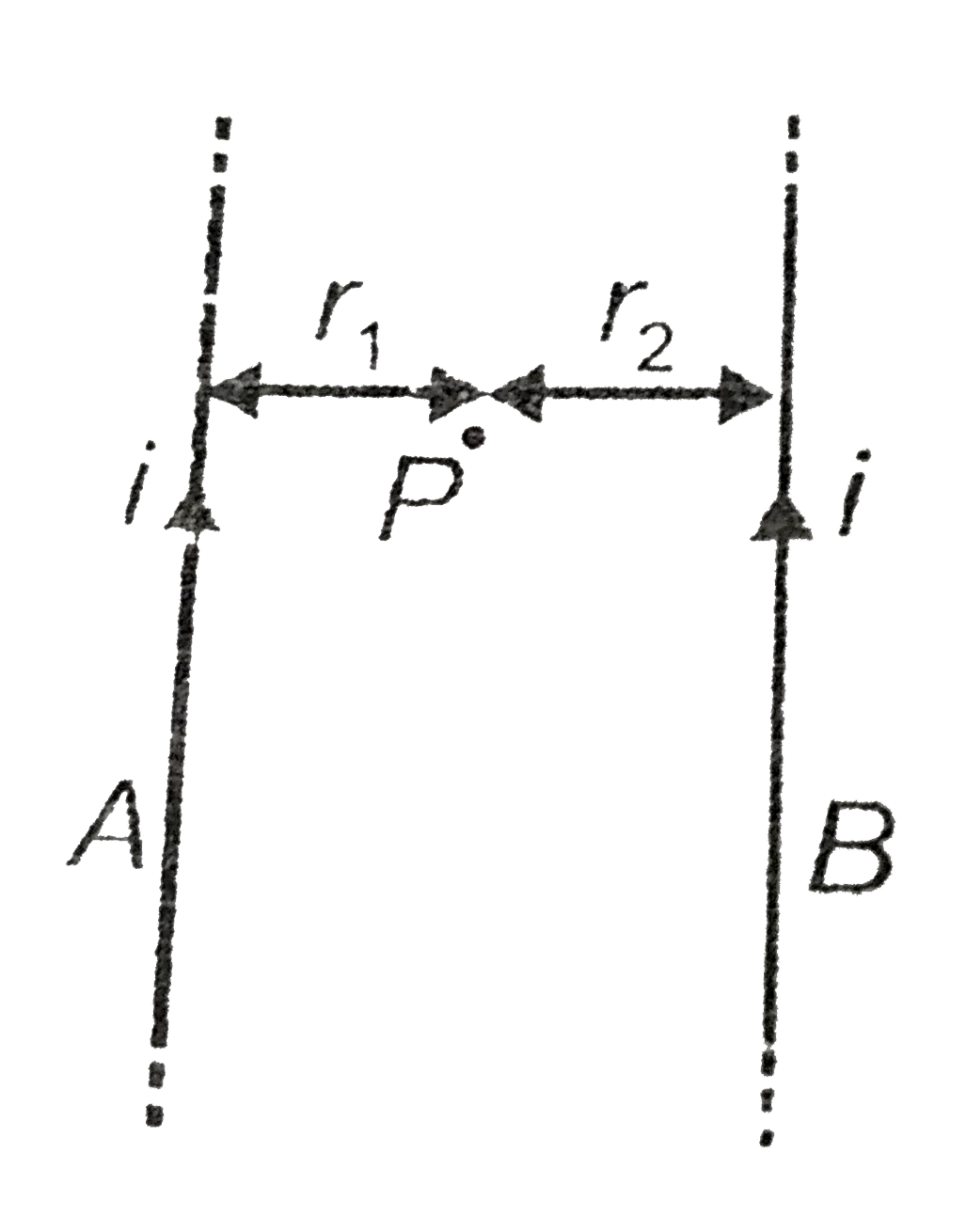
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure below

View SolutionAn infinite number of charges, each of coulomb, are placed along x-axis at x=1m,3m,9m and so on. Calculate the electric field at the point x = 0 due to these charges if all the charges are of the same sign.
View SolutionFind the direction of magnetic field at a point P due to two infinite current carrying wires shown in the figure. Given r1>r2
View SolutionThe electric field on two sides of a thin sheet of charge is shown in the figure. The charge density on the sheet is
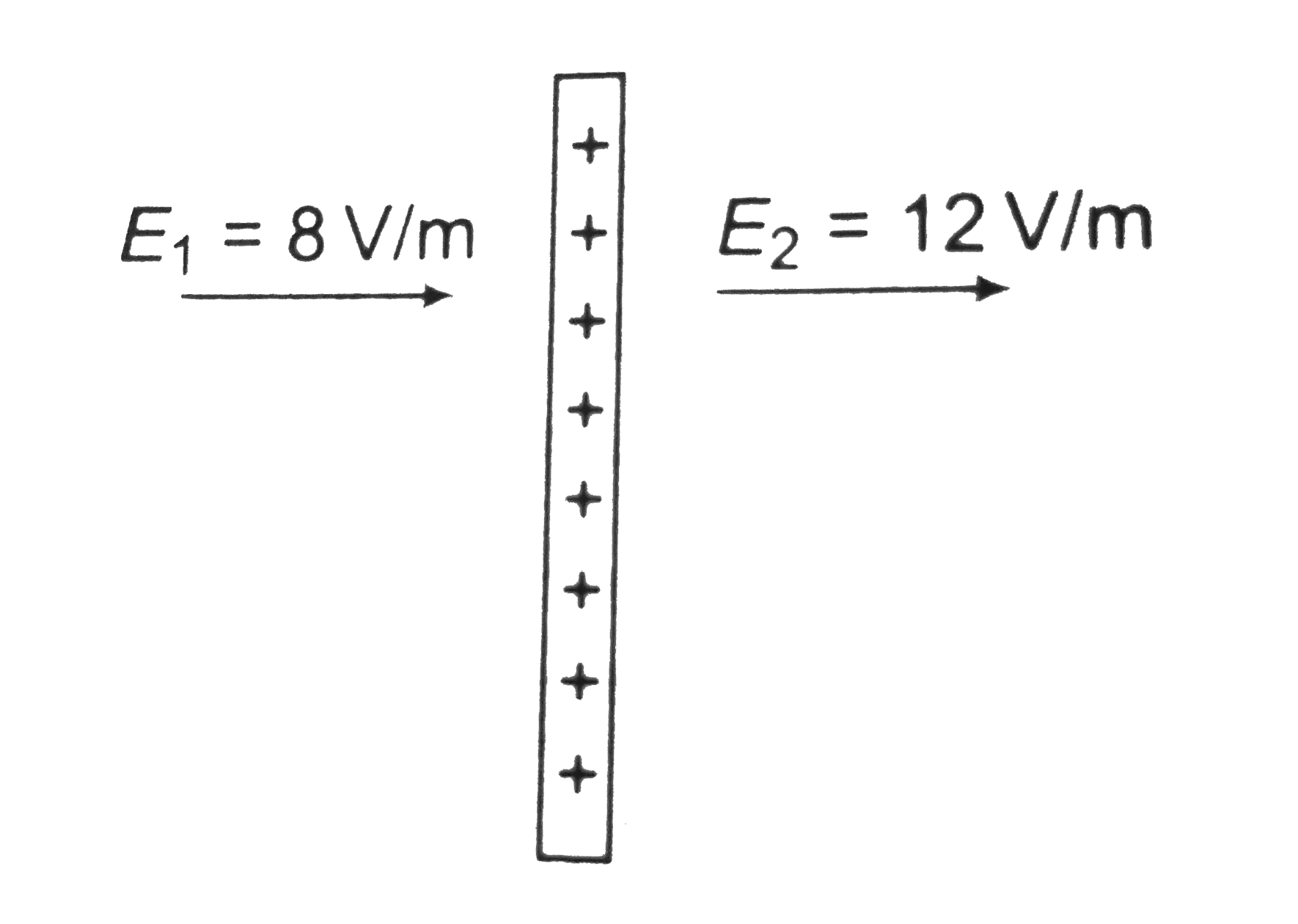
View SolutionThe spatial distribution of the electric field due to charges (A,B) is shown in figure. Which of the following statements is correct?

View SolutionA charge particle q is projected in an electric field produced by a fixed point charge Q as shown in figure. Mark the correct statements.

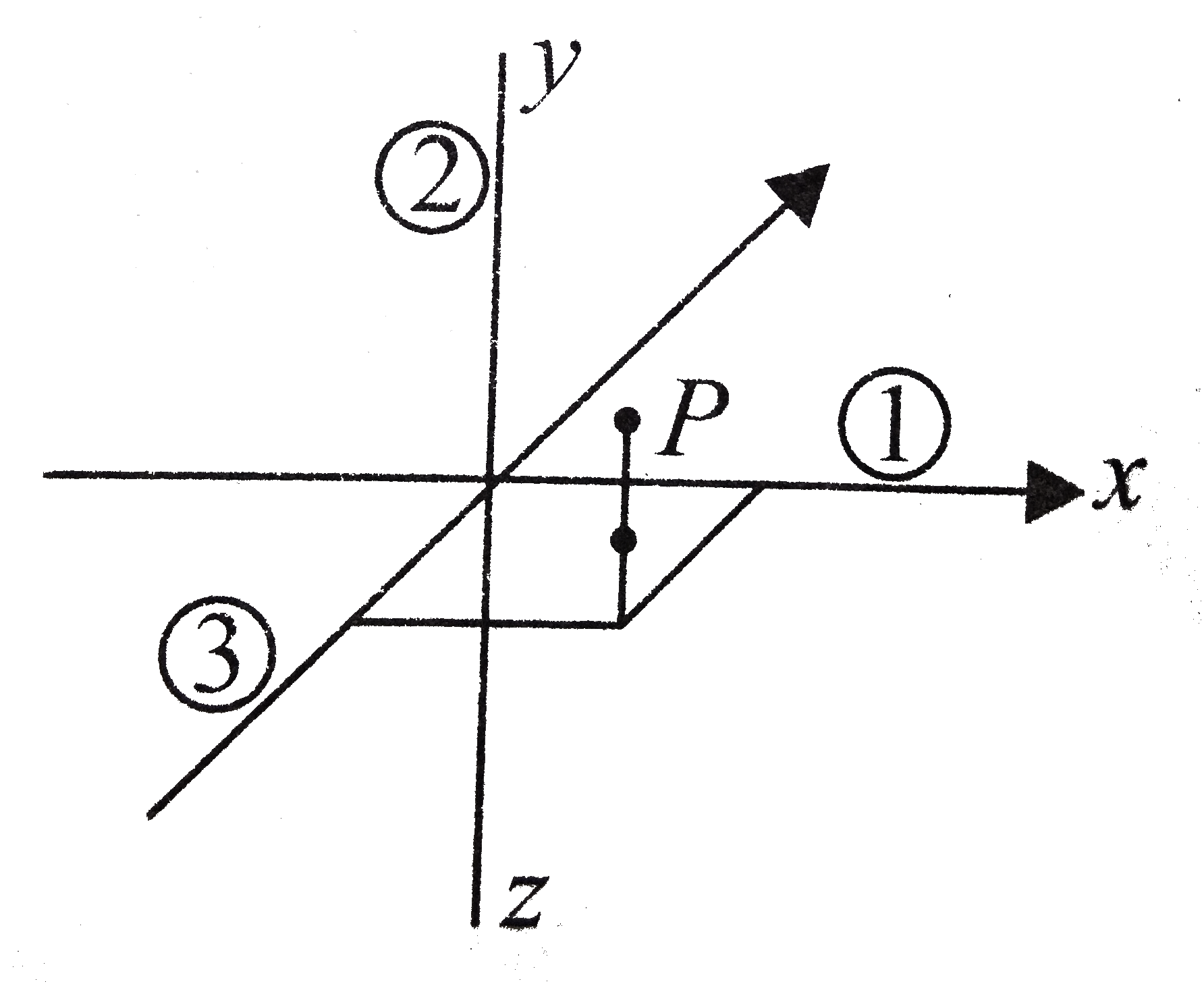
View SolutionFind the electric field vector at P (a,a,a) due to three infinitely long lines of charges along the x-, y- and z-axis, respectively. The charge density i.e. charge per unit length of each wire is (λ),
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in figure. The y−andz−compo≠nts of the electric field are zero in this region. If the electric potential is 10 V at the origin, then the potential at x = 2.0 m is
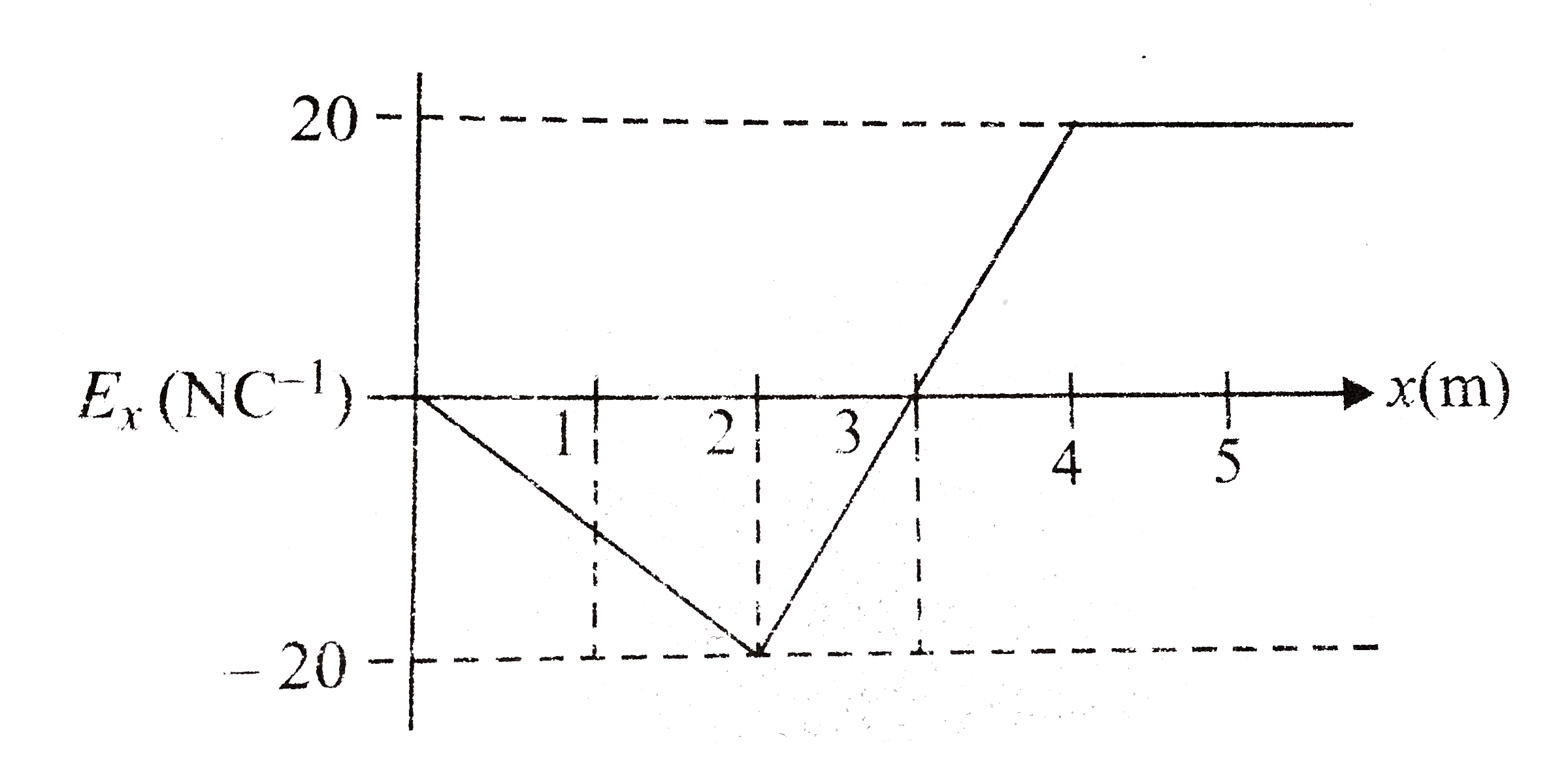
View SolutionA graph of the x-component of the electric field as a function of x in a region of space is shown in the figure. They y and z-components of the electric field are zero in this region. The electric potential at the origin is 10 V. The value of x for which potential is zero is
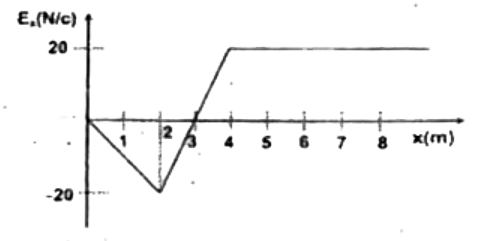
View Solution