It is known that the time of revolution T of a satellite around the earth depends on the universal gravitational constant G, the mass of the earth M, and the radius of the circular orbit R. Obtain an expression for T, dimensional analysis.
We have [T]=[G]a[M]a[R]c
[M]0[L]0[T]1=[M]−a[L]3a[T]−2a×[M]b×[L]c=[M]b−a[L]c+3a[T]−2a
Comparing the exponents
For [T]:1=−2a⇒a=−12
For [M]:0=b−a⇒b=a=−12
For [L]:0=c+3a⇒c=−3a=32
Putting the values we get T∝G−1/2M−1/2R3/2∝√R3GM
The actual expression is T=2π√R3GM
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example
61 Videos
- MISCELLANEOUSBOOK - ALLENCHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Video
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLENCHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLENCHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
8 Videos
Similar Questions
It is known that the time of revolution T of a satellite around the earth depends on the universal gravitational constant G, the mass of the earth M, and the radius of the circular orbit R. Obtain an expression for T using dimensional analysis.
View SolutionThe escape velocity of a sphere of mass m is given by (G= univesal gravitational constant, Me= mass of the earth and Re= radius of the earth)
View Solution
Knowledge Check
Match the Column I with Column II
For a satellite in circular orbit
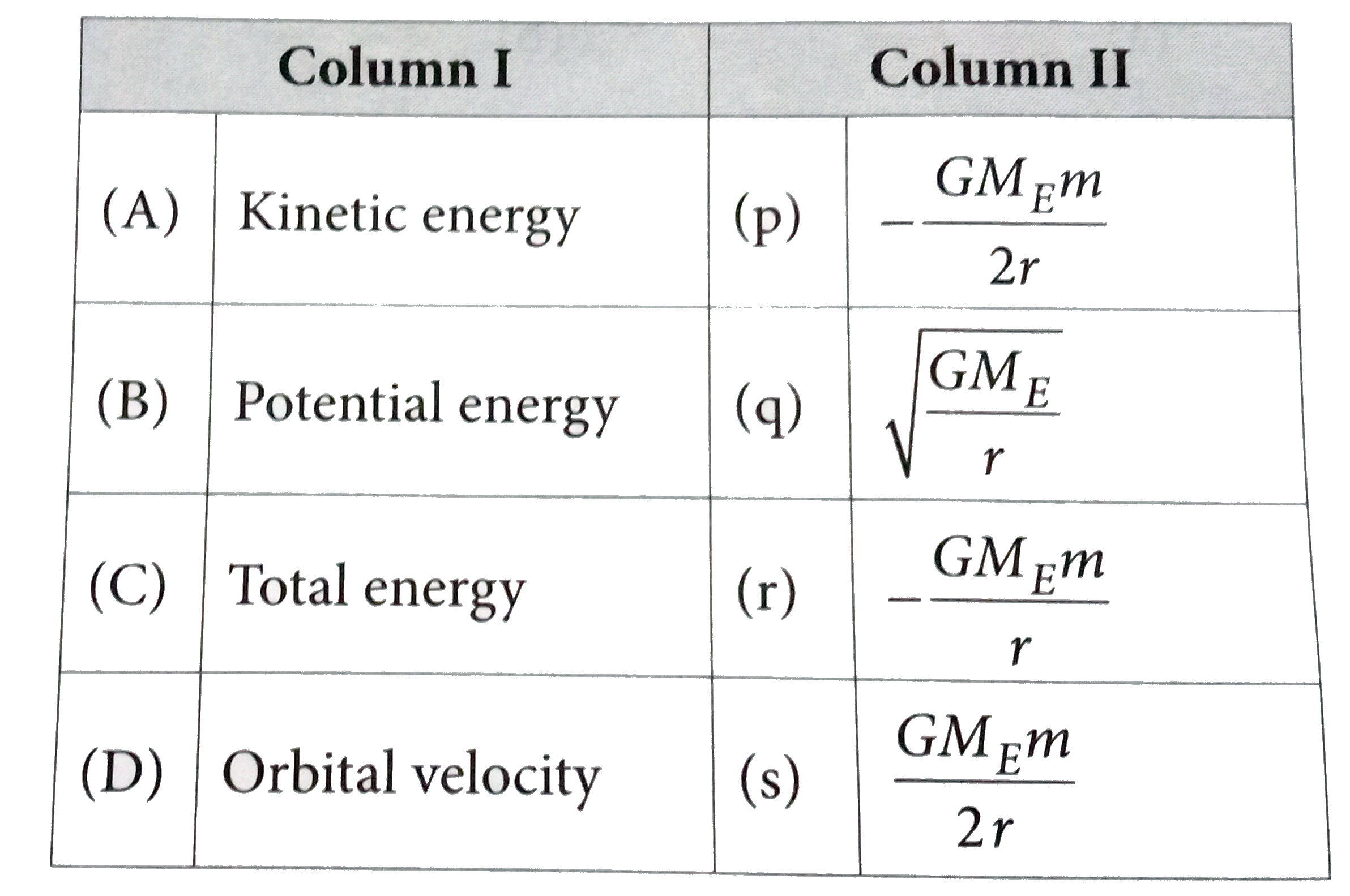
(where ME is the mass of the earth , m is the mass of the satellite and r is the radius of the orbit )AA-r, B-s,C-q,D-pBA-q,B-p,C-r,D-sCA-p,B-q,C-s,D-rDA-s,B-r,C-p,D-qA satellite is orbiting the earth in a circular orbit of radius r. Its
AKnetic enegy varies as rBangular momentum varies as 1√rClinear momentum varies as 1rDfrequency of revolution varies as 1r3/2
Length of a year on a planet is the duration in which it completes one revolution around the sun. Assume path of the planet known as orbit to be circular with sun at the centre. The length T of a year of a planet orbiting around the sun in circular orbit depends on universal gravitational constant G, mass ms of the sun and radius r of the orbit. if T∝Gambsrc find value of a+b+2c.
View SolutionThe acceleration due to gravity at a piece depends on the mass of the earth M, radius of the earth R and the gravitational constant G. Derive an expression for g?
View SolutionThe period of revolution of a satellite depends upon the radius of the orbit, the mass of the planet and the gravitational constant. Prove that the square of the period varies as the cube of the radius.
View SolutionThe escape velocity of a body from the surface of the earth depends upon (i) the mass of the earth M, (ii) The radius of the eath R, and (iii) the gravitational constnat G. Show that v=k√GMR, using the dimensional analysis.
View SolutionA satellite moves around the earth in a circular orbit with speed v. If m is the mass of the satellite, its total energy is
View SolutionA satellite of mass m goes round the earth along a circular path of radius r. Let mE be the mass of the earth and RE its radius then the linear speed of the satellite depends on.
View Solution
