A particle of mass 2 kg moving with a velocity 5ˆims−1 collides head-on with another particle of mass 3kg moving with a velocity −2ˆims−1. After the collision the first particle has speed of 1.6ms−1 in negative x-direction. Find
(i) velocity of the center of mass after the collision
(ii) velocity of the second particle after the collision
(iii) coefficient of restitution.
The correct Answer is:(i) 0.8ˆims−1 (ii) 2.4ˆims−1 (c ) 47
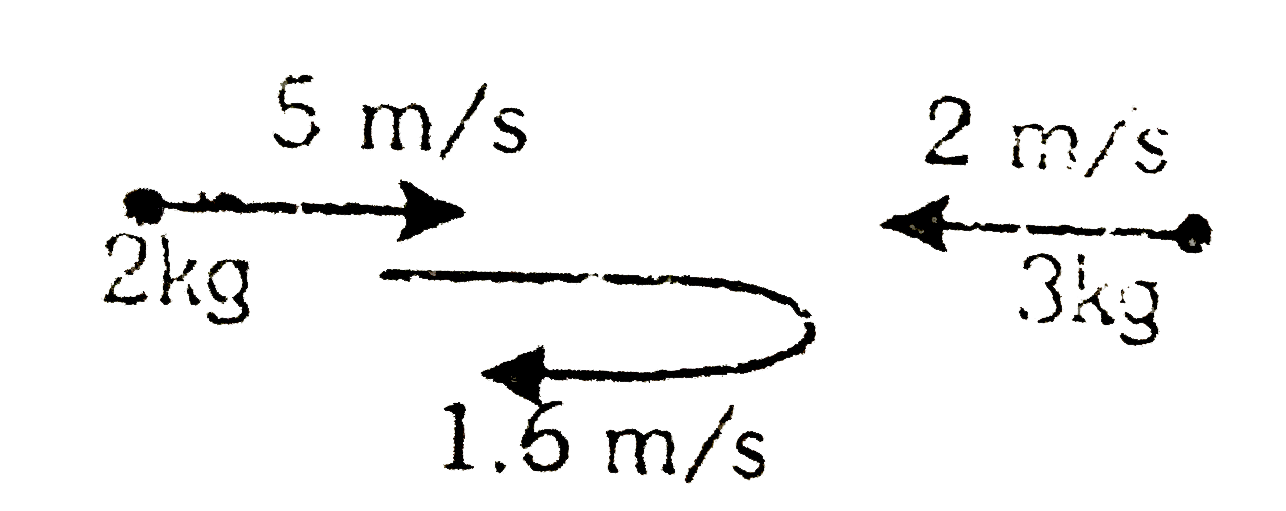
(A) vcm=[(2×5)−(3×2)2+3]ˆi=45ˆim/s
(B) COLM⇒(2×5)+3(−2)=+2(−1.6)+3v2⇒v2=2.4m/s
(C ) e=−(v2−v1u2−u1)=47
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
42 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A particle of mass 2kg moving with a velocity 5ˆim/s collides head-on with another particle of mass 3kg moving with a velocity −2ˆim/s. After the collision the first particle has speed of 1.6m/s in negative x-direction, Find
(a) velocity of the centre of mass after the collision,
(b) velocity of the second particle after the collision.
(c) coefficient of restitution.
View SolutionA particle of mass 2kg moving with a velocity 5ˆim/s collides head-on with another particle of mass 3kg moving with a velocity −2ˆim/s. After the collision the first particle has speed of 1.6m/s in negative x-direction, Find
(a) velocity of the centre of mass after the collision,
(b) velocity of the second particle after the collision.
(c) coefficient of restitution.
View Solution
Knowledge Check
A particle of mass 1 g moving with a velocity →v1=3ˆi−2ˆjms−1 experiences a perfectly in elastic collision with another particle of mass 2 g and velocity →v2=4ˆj−6ˆkms−1. The velocity of the particle is
A2.3ms−1B4.6ms−1C9.2ms−1D6ms−1
A particle of mass m moving with a velocity (3ˆi+2ˆj)ms−1 collides with another body of mass M and finally moves with velocity (−2ˆi+ˆj)ms−1. Then during the collision
View SolutionA particle of mass 1031kg is moving with a velocity equal to 105ms−1. The wavelength of the particle is equal to
View SolutionA ball of mass m moving with velocity v collides head on elastically with another identical ball moving with velocity - V. After collision
View SolutionA particle of mass m1=4kg moving at 6ˆims−1 collides perfectly elastically with a particle of mass m2=2 moving at 3ˆims−1
View SolutionAn object of mass 80 kg moving with velocity 2ms−1 hit by collides with another object of mass 20 kg moving with velocity 4ms−1 Find the loss of energy assuming a perfectly, inelastic collision
View SolutionAn object of mass 80 kg moving with velocity 2ms−1 hit by collides with another object of mass 20 kg moving with velocity 4ms−1 Find the loss of energy assuming a perfectly, inelastic collision
View SolutionA body of mass 2kg moving with a velocity 3m/s collides with a body of mass 1kg moving with a velocity of 4m/s in opposite direction. If the collision is head on and completely inelastic, then
View Solution
