One particle of mass 1 kg is moving along positive x-axis with velocity 3 m/s. Another particle of mass 2 kg is moving along y-axis with 6 m/s. At time t=0, 1 kg mass is at (3 m,0) and 2 kg at (0,9 m). x-y plane is the horizontal plane. (surface is smooth for question 15 and rough for questions 16 and 17).
The centre of mass of the two particles is moving in a straight line
y=x+2
y=4x+2
y=2x−4
y=2x+4
The correct Answer is:B
→rcm=m1→r10+m2→r2m1+m2=1(3ˆi)+2(9ˆj)1+2=(ˆi+6ˆj)m
→vcm=m1→v1+m2→v2m1+m2=1(3ˆi)+2(6ˆj)1+2(ˆi+4ˆj)m/s
Now Δ→rcm=→vcmt⇒→rcm−→rcm0=→vcmt
⇒(x−1)ˆi+(y−6)ˆj=(ˆi+4ˆj)t
⇒x=1+t and y=6+4t⇒y=4x+2
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Comprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
The centre of mass of the two particles is moving in a straight line for which equation is :
View SolutionComprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is smooth for question 1 and rough for question 2 and 3)
If both the particles have the same value of coefficient of friction μ=0.2. The centre of mass will stop at time t= ..........s :-
View SolutionComprehension # 5
One particle of mass 1kg is moving along positive x-axis with velocity 3m/s. Another particle of mass 2kg is moving along y-axis with 6m/s. At time t=0,1kg mass is at (3m,0) and 2kg at (0,9m),x−y plane is the horizontal plane. (Surface is rough for question, if cofficient of friction is 0.2 in both axis)
Co-ordinates of center of mass where it will stop finally are :-
View SolutionA particle of mass m1=4kg moving at 6ˆims−1 collides perfectly elastically with a particle of mass m2=2 moving at 3ˆims−1
View SolutionA block of mass 1kg is at x=10m and moving towards negative x−aξs with velocity 6m/s. Another block of mass 2kg is at x=12m and moving towards positive x−axis with velocity 4m/s at the same instant. Find position of their centre of mass after 2s.
View SolutionThe position (X)-time (t) graph for a particle of mass 1 kg moving along x-axis is shown in figure. Find impulse on particle at t = 4 s.
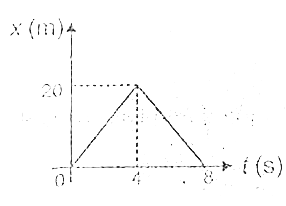
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionTwo particles of masses 1kg and 2kg are located at x=0 and x=3m. Find the position of their centre of mass.
View SolutionA particle of mass 2 kg moving with a speed of 6 m/s collides elastically with another particle of mass 4 kg travelling in same direction with a speed of 2m/s. The maximum possible deflection of the 2 kg particle is
View SolutionA ball of mass 1kg moving with 4m−1 along +x-axis collides elastically with an another ball of mass 2kg moving with 6m/s is opposite direction. Find their velocities after collision.
View Solution