An impulse changes the velocity of a particle from to . Kinetic energy gained by the particle is :-
The correct Answer is:A
To solve the problem of finding the kinetic energy gained by a particle when its velocity changes from →v1 to →v2 due to an impulse →I, we can follow these steps:
Step 1: Understand the formula for kinetic energy
The kinetic energy (KE) of a particle is given by the formula:
KE=12mv2
where m is the mass of the particle and v is its velocity.
Step 2: Write the expression for initial and final kinetic energy
The initial kinetic energy (KE1) when the particle has velocity →v1 is:
KE1=12mv21
The final kinetic energy (KE2) when the particle has velocity →v2 is:
KE2=12mv22
Step 3: Calculate the change in kinetic energy
The change in kinetic energy (ΔKE) is given by:
ΔKE=KE2−KE1=12mv22−12mv21
This can be factored as:
ΔKE=12m(v22−v21)
Step 4: Use the identity for the difference of squares
We can use the identity a2−b2=(a−b)(a+b) to rewrite the expression:
v22−v21=(v2−v1)(v2+v1)
Thus, we can express the change in kinetic energy as:
ΔKE=12m(v2−v1)(v2+v1)
Step 5: Relate impulse to change in momentum
Impulse →I is defined as the change in momentum:
→I=m→v2−m→v1=m(→v2−→v1)
From this, we can express the change in velocity in terms of impulse:
→v2−→v1=→Im
Step 6: Substitute impulse into the kinetic energy equation
Substituting →v2−→v1 into the change in kinetic energy equation gives:
ΔKE=12m(→Im)(→v2+→v1)
This simplifies to:
ΔKE=12→I(→v2+→v1)
Conclusion
Thus, the kinetic energy gained by the particle is:
ΔKE=12→I(→v2+→v1)
The kinetic energy (KE) of a particle is given by the formula:
KE=12mv2
where m is the mass of the particle and v is its velocity.
The initial kinetic energy (KE1) when the particle has velocity →v1 is:
KE1=12mv21
The final kinetic energy (KE2) when the particle has velocity →v2 is:
KE2=12mv22
The change in kinetic energy (ΔKE) is given by:
ΔKE=KE2−KE1=12mv22−12mv21
This can be factored as:
ΔKE=12m(v22−v21)
We can use the identity a2−b2=(a−b)(a+b) to rewrite the expression:
v22−v21=(v2−v1)(v2+v1)
Thus, we can express the change in kinetic energy as:
ΔKE=12m(v2−v1)(v2+v1)
Impulse →I is defined as the change in momentum:
→I=m→v2−m→v1=m(→v2−→v1)
From this, we can express the change in velocity in terms of impulse:
→v2−→v1=→Im
Substituting →v2−→v1 into the change in kinetic energy equation gives:
ΔKE=12m(→Im)(→v2+→v1)
This simplifies to:
ΔKE=12→I(→v2+→v1)
Thus, the kinetic energy gained by the particle is:
ΔKE=12→I(→v2+→v1)
Topper's Solved these Questions
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-II
Explore 43 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-III
Explore 42 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-V B
Explore 19 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS Book:ALLENChapter:BASIC MATHEMATICS USED IN PHYSICS &VECTORS Exercise:EXERCISE-IV ASSERTION & REASON
Explore 11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 5 B (Integer Type Questions)
Explore 3 Videos
Similar Questions
If a particle is moving as →r=(→i+2→j)cosω0t then,motion of the particleis
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View Solution
Knowledge Check
A charged particle with charge q enters a region of constant, uniform and mututally orthogonal fields →Eand→B with a velocity →v perpendicular to both →Eand→B, and comes out without any change in magnitude or direction of →v. Then
A→v=→B×→E/E2B→v=→E×→B/B2C→v=→B×→E/B2D→v=→E×→B/E2
If →v1+→v2 is perpendicular to →v1−→v2, then
View SolutionA particle is moving on a circular path such that at any instant its position vector, linear velocity. Angular velocity, angular acceleration with respect to centre are →r,→v,→w,→α respectively. Net acceleration of the particle is :−
View SolutionThe position vector of a particle of mass m= 6kg is given as →r=[(3t2−6t)ˆi+(−4t3)ˆj]m. Find:
(i) The force (→F=m→a) acting on the particle.
(ii) The torque (→τ=→r×→F) with respect to the origin, acting on the particle.
(iii) The momentum (→p=m→v) of the particle.
(iv) The angular momentum (→L=→r×→p) of the particle with respect to the origin.
View SolutionA particle of m=5kg is momentarily at rest at x=att=. It is acted upon by two forces →F1 and →F2. Vec(F)1=70ˆj N. The direction and manitude of →F2 are unknown. The particle experiences a constant acceleration, →a,in the direction as shown in (figure) Neglect gravity.
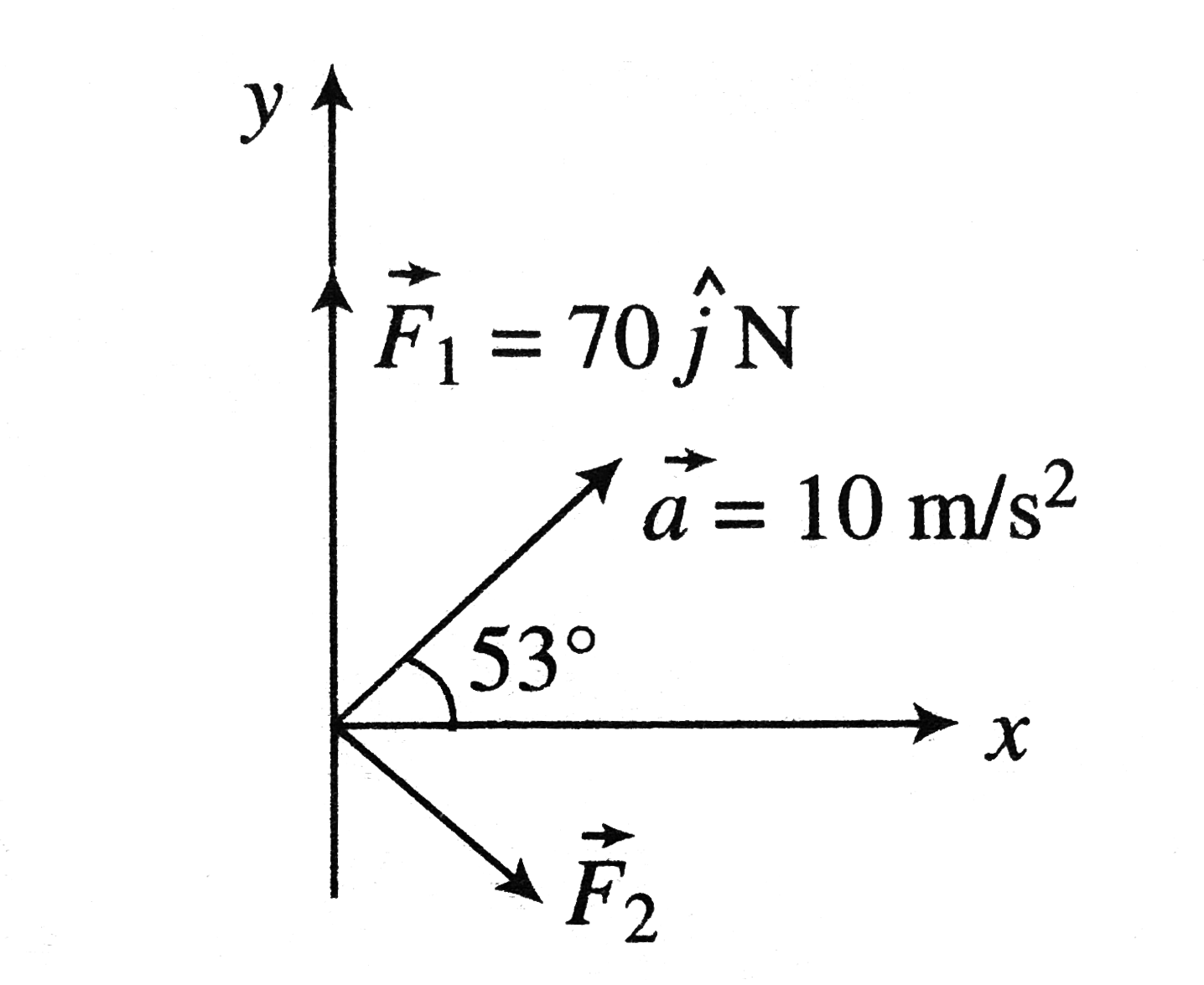
a.Find the missing force →F2.
b. What is the velocity vector of the particle at t=10s?
c. What third force, →F3 is required to make the acceleration of the particle zero? Either give magnitude and direction of →F3 or its components.
View SolutionA particle moves with a tangential acceleration at=→a.ˆv where →a=(5ˆi)m/s2. If the speed of the particle is zero at x=0, then find v (in m/s) at x=4.9m.

View SolutionA particle of specific charge q/m=(π)C/kg is projected from the origin towards positive x-axis with a velocity of 10m/s in a uniform magnetic field →B=−2ˆK Tesla. The velocity →V of the particle after time t=1/6 s will be
View SolutionA particle of specific charge q/m=(π)C/kg is projected from the origin towards positive x-axis with a velocity of 10m/s in a uniform magnetic field →B=−2ˆK Tesla. The velocity →V of the particle after time t=1/6 s will be
View Solution