Considering a system having two masses m1 and m2 in which first mass is pushed towards centre of mass by a distance a, the distance required to be moved for second mass to keep centre of mass at same position is :-

m1m2a
m1m2a
m2m1a
(m2m1m1+m2)a
The correct Answer is:A
Δ¯x=m1.Δx1+m2.Δx2m1+m2
⇒0=m1a+m2Δx2m1+m2
⇒Δx2=−m1am2
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-II
43 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
42 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLENCHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Consider a two particle system with the particles having masses m1andm2. If the first particles pushed towards the centre of mass through a distance d, by what distance should the second particle be moved so as the keep the centre of mass at the same position?
View SolutionConsider a system of two particles having masses m1 and m2. If the particle of mass m1 is pushed towards the centre of mass of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the mass centre of particles at the original position?
View Solution
Knowledge Check
Two stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
A2π√r32G(m1+m2)B2π√r3(m1+m2)2G(m1m2)C2π√2r3G(m1+m2)D2π√r3G(m1+m2)
Consider a sytem of two particles having masses m1 and m2. If the particle of mass m1 is pushed towards the centre of mass of particles through a distance d, by what distance would the particle of mass m2 move so as to keep the mass centre of particles at the original position?
View SolutionConsider a system of two particles having masses 2kg and 5 kg the particle of mass 2 kg is pushed towards the centre of mass of particles through a distance 5 m,by what distance would particle of mass 5kg move so as to keep the centre of mass of particles at the original position?
View SolutionCalculate centre of mass of the system
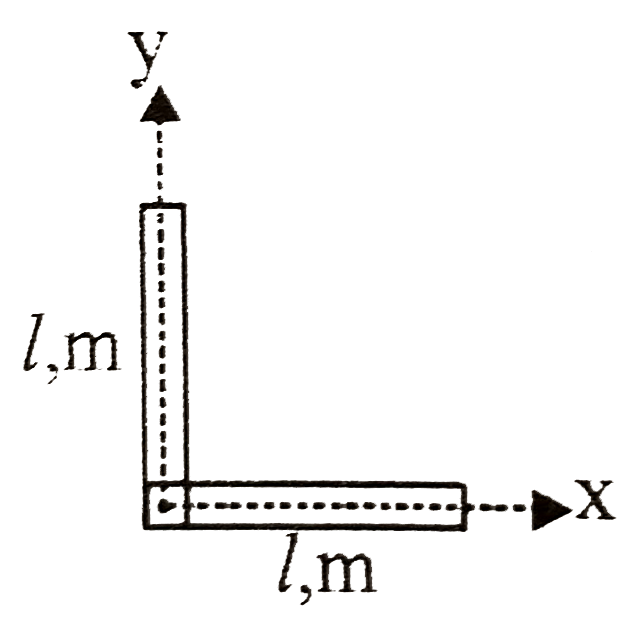
View SolutionTwo bocks of masses 10 g and 20 kg are plced on the X-axis. The first mass is moved on the axis by a distance of 2 cm. By what distance should the second mass be moved to keep the position of the centre of mass unchanged?
View SolutionTwo stars of masses m1 and m2 distance r apart, revolve about their centre of mass. The period of revolution is :
View SolutionAssertion : Position of centre of mass is independent of the reference frame
. Reason : Centre of mass is same for all bodies
View SolutionA body of mass m moving with a velocity v is approaching a second object of same mass but at rest. The kinetic energy of the two objects as viewed from the centre of mass is
View Solution
