If magnetic field in space is 1Tˆi, electric field is 10N/Cˆi, no gravitational field is present and a charged particle is released from rest from origin, it will
not move at all
move in circular path
move in a helical path
move on a straight line
The correct Answer is:D
To solve the problem, we need to analyze the forces acting on a charged particle released from rest in the presence of electric and magnetic fields.
1. Identify the Given Information:
- Magnetic field, →B=1Tesla in the direction of ^i.
- Electric field, →E=10N/C in the direction of ^i.
- The particle is released from rest at the origin.
2. Determine the Forces Acting on the Charged Particle:
- The force due to the electric field on a charge Q is given by:
→FE=Q→E=Q⋅10^i=10Q^i
- The magnetic force on a charge moving with velocity →V in a magnetic field →B is given by:
→FB=Q(→V×→B)
- Since the particle is released from rest, its initial velocity →V=0. Therefore, the magnetic force is:
→FB=Q(0×→B)=0
3. Analyze the Motion of the Charged Particle:
- The only force acting on the charged particle is the electric force →FE=10Q^i.
- Since there is no magnetic force acting on the particle (as it is at rest), the particle will start to accelerate in the direction of the electric field.
4. Conclusion:
- The charged particle will move in the direction of the electric field (along ^i) with an increasing velocity due to the constant electric force acting on it.
- Since there is no magnetic force acting on it, it will continue to move in a straight line.
Final Answer:
The charged particle will move in a straight line along the direction of the electric field.
- Magnetic field, →B=1Tesla in the direction of ^i.
- Electric field, →E=10N/C in the direction of ^i.
- The particle is released from rest at the origin.
- The force due to the electric field on a charge Q is given by:
→FE=Q→E=Q⋅10^i=10Q^i
- The magnetic force on a charge moving with velocity →V in a magnetic field →B is given by:
→FB=Q(→V×→B)
- Since the particle is released from rest, its initial velocity →V=0. Therefore, the magnetic force is:
→FB=Q(0×→B)=0
- The only force acting on the charged particle is the electric force →FE=10Q^i.
- Since there is no magnetic force acting on the particle (as it is at rest), the particle will start to accelerate in the direction of the electric field.
- The charged particle will move in the direction of the electric field (along ^i) with an increasing velocity due to the constant electric force acting on it.
- Since there is no magnetic force acting on it, it will continue to move in a straight line.
The charged particle will move in a straight line along the direction of the electric field.
Topper's Solved these Questions
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:Part-1 Physics
Explore 15 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:part-2 physics
Explore 71 Videos
- TEST PAPERSBook:ALLENChapter:TEST PAPERSExercise:PAPER 2
Explore 60 Videos
- TEST PAPER 4Book:ALLENChapter:TEST PAPER 4Exercise:PHYSICS
Explore 44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
Similar Questions
The acceleration of a charged particle in a uniform electric field is
View SolutionIn a region, steady and uniform electric and magnetic fields are present . These two fields are parallel to each other. A charged particle is released from rest in this region . The path of the particle will be a
View SolutionIn a region where both non-zero uniform electric field and magnetic field coexist, the path of a charged particle
View SolutionIn a region of space uniform electric field is present as →E=E0ˆi and uniform magnetci field is present as →B=−B0ˆj . An electron is released from rest at origin. What is the path followed by electron after released. (E0&B0are positive constants )
View SolutionElectric and magnetic field are directed as E0ˆi and B0ˆk, a particle of mass m and charge + q is released from position (0,2,0) from rest. The velocity of that particle at (x,5,0) is (5ˆi+12ˆj) the value of x will be
View SolutionElectric field and magnetic field n a region of space is given by E=E0ˆj and B=B0ˆj. A particle of specific charge alpha is released from origin with velocity v=v0ˆi. Then path of particle
View SolutionIn a region of crossed fields as shown, the strength of electric field is E and that of magnetic field is B. Three positively charged particles with speeds V1,V2andV3 are projected and their paths are shown. From this it implies that
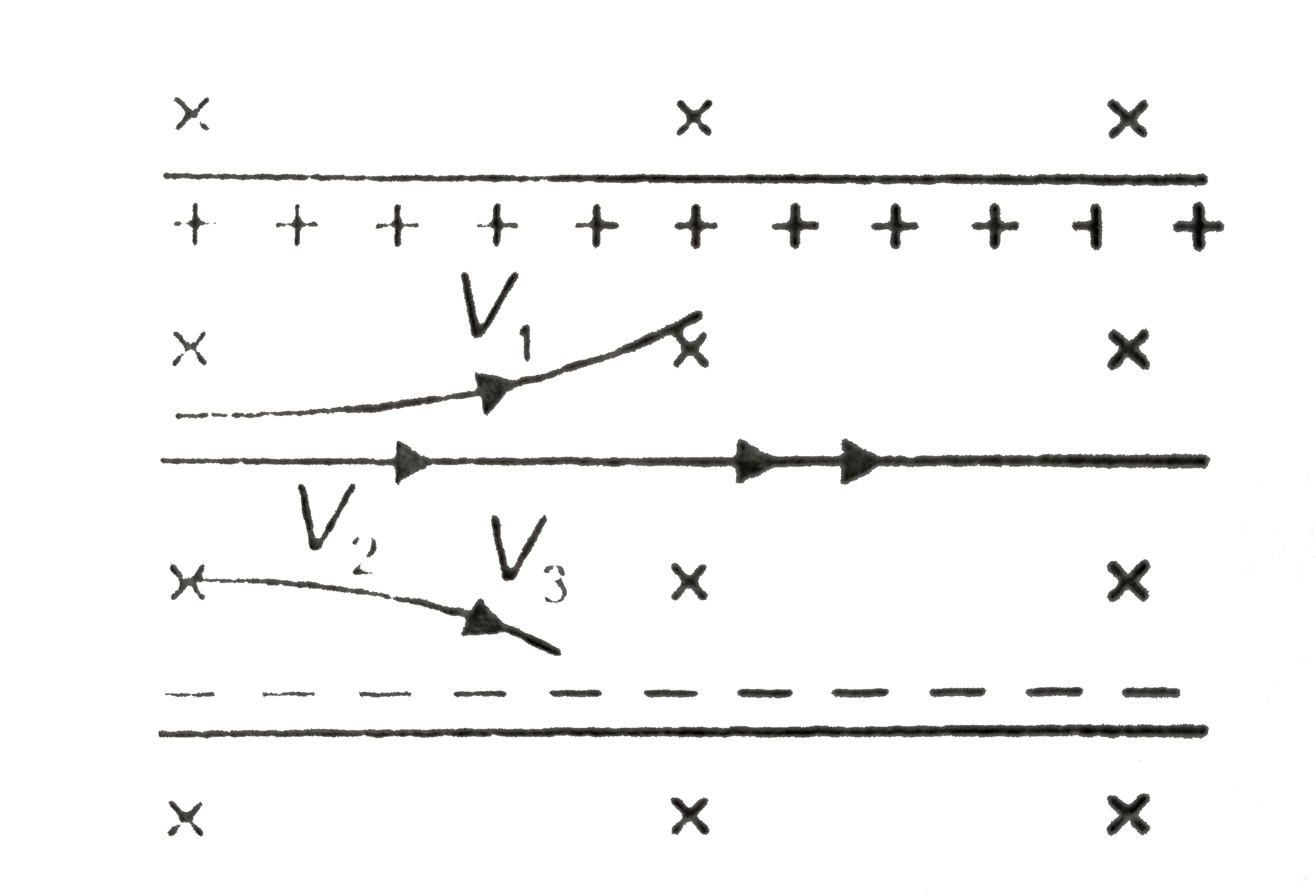
View SolutionElectric field and magnetic field in a region of space are given by(Ē=E0ˆj). and (¯¯¯B=B0ˆj). A charge particle is released at origin with velocity (¯v=v0ˆk) then path of particle is
View SolutionIf a charged particle enters perpendicular in the uniform magnetic field then
View SolutionA particle moves in a region having a uniform magnetic field and a parallel, uniform electric field. At some instant, the velocity of the particle is perpendicular to the field direction. The path of the particle will be
View Solution