Two bodies of masses 2kg and 3kg are connected by a metel wire of cross section 0.04 mm2. Breaking stress of metel wire is 2.5 Gpa. The maximum force F that can be applied to 3kg block so that wire does not break is :

100N
150N
200N
250N
The correct Answer is:D

TA=2.5×109
T=(2.5×109)A
T=2.5×109×0.04×10−6=100
Then maximum acceleration of block 2kg is = 50m/sec3
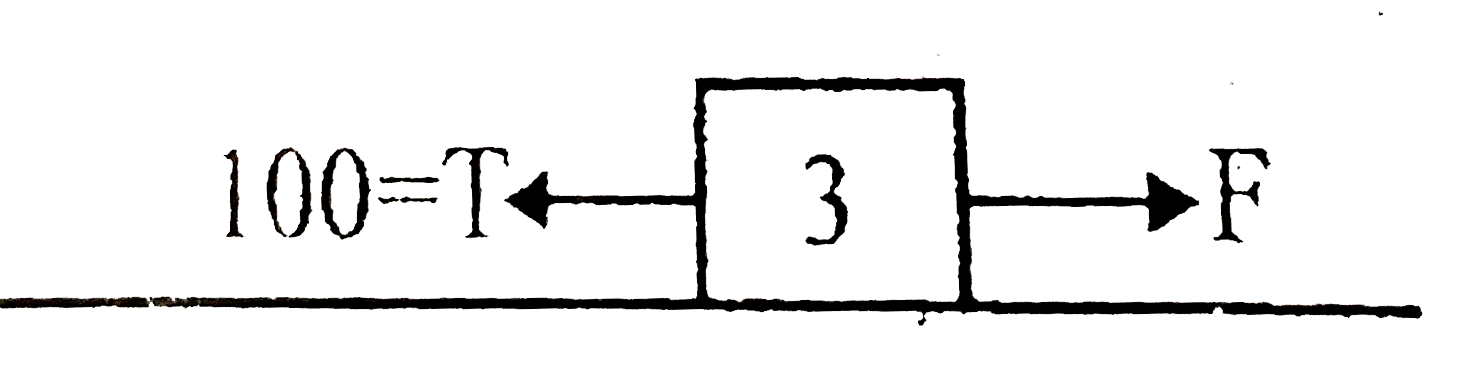
F-T=ma
F=T+ma=100+3×50=250N
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPERSBOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - PAPER 3
99 Videos
- TEST PAPER 4BOOK - ALLENCHAPTER - TEST PAPER 4EXERCISE - PHYSICS
44 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
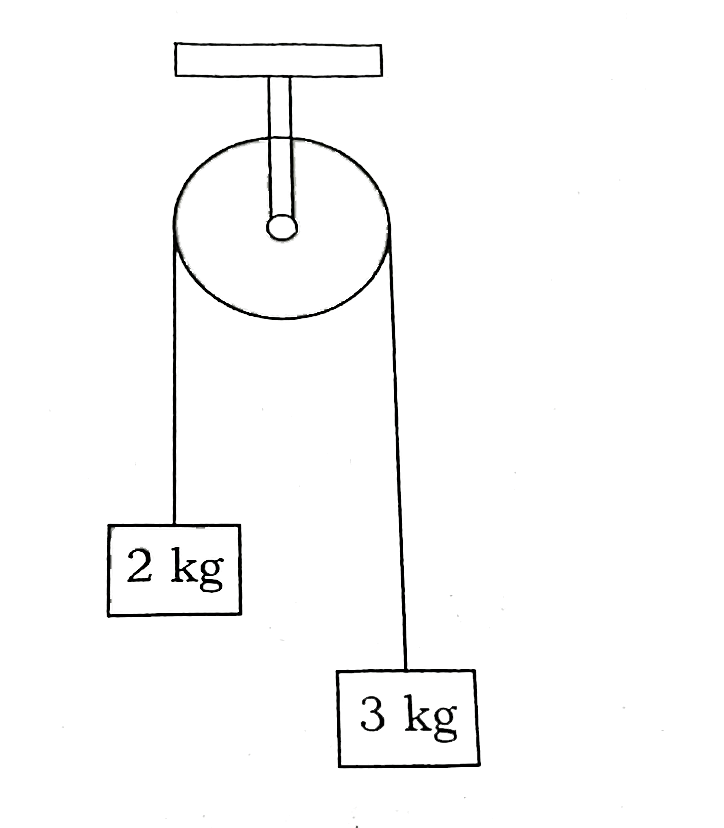
Two blocks of masses 2 kg and 3kg are connected by a metal wire going over a smoother pulley as shown in figure. The breaking stress of the steel is 2×109Nm−2. What would be the minimum radius of the wire used if it not to break ? Take ,g=10ms−2
View SolutionTwo blocks of masses 1 kg and 2kg are connect by a metal wire going over a smooth pulley as shown in figure. The breaking stress of the metal is 2×109Nm−2. What should be the minimum radius of the wire used if it is not to break? Take g=10ms−2
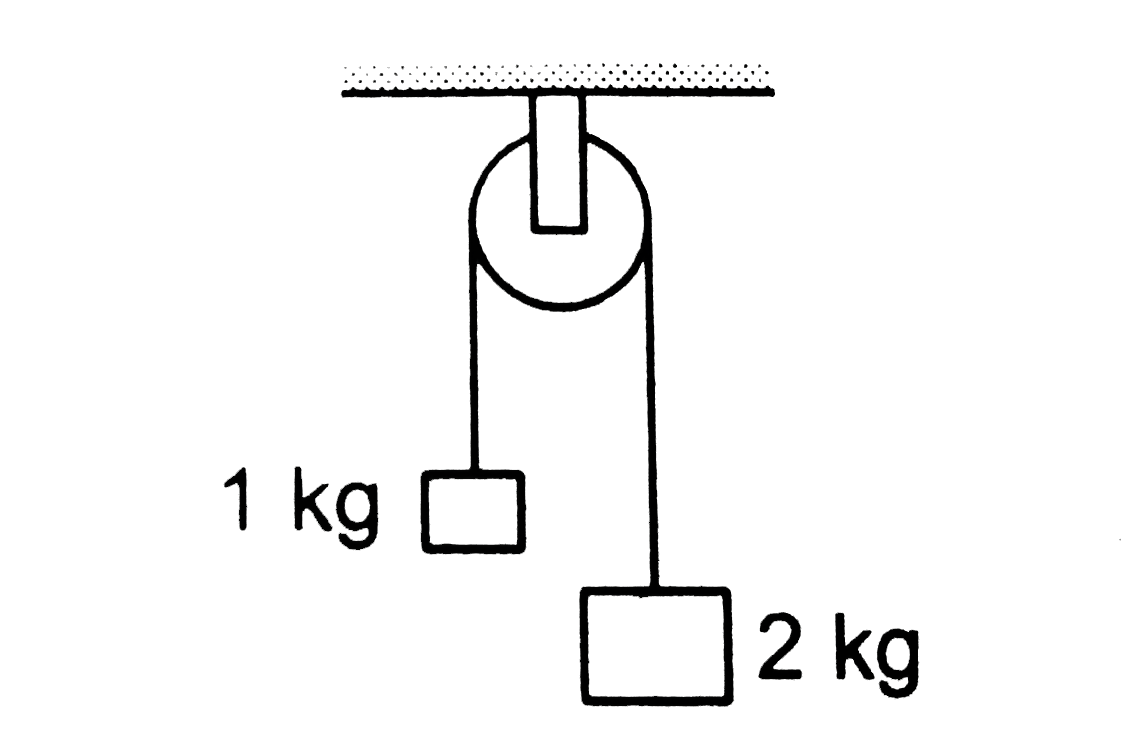
View Solution
Knowledge Check
Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
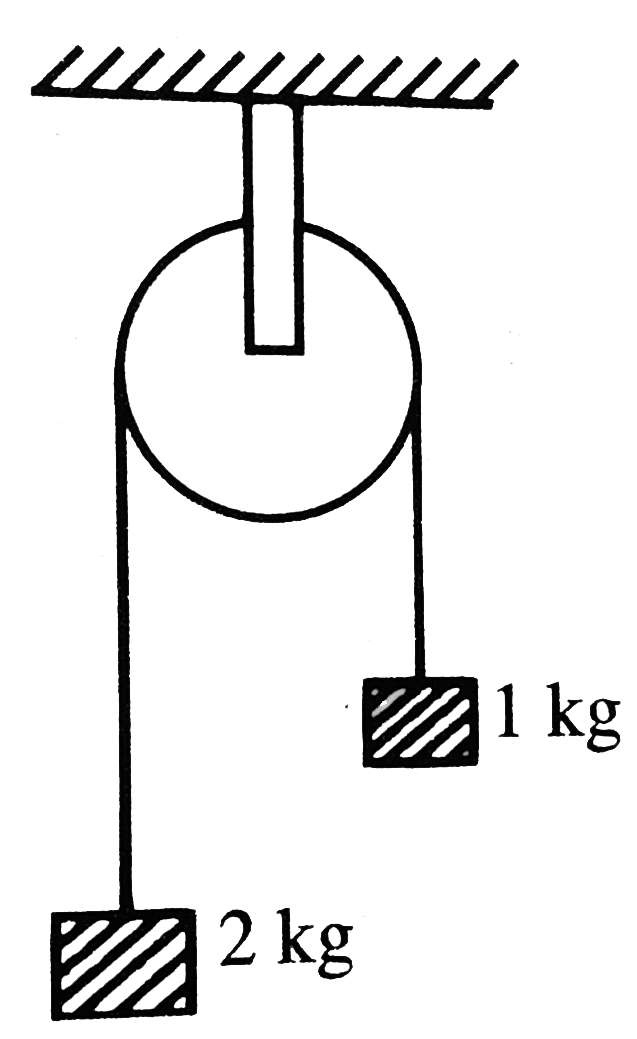
A100NB200NC300ND400NTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?
 A0.5 mmB1 mmC1.5 mmD2 mm
A0.5 mmB1 mmC1.5 mmD2 mm
Two blocks of masses 5 kg and 10 kg are connected by a metal wire going over a smooth pulley as shown in the figure. The breaking stress of the metal wire is 2×109N m−2. If g=10ms−2, then what is the minimum radius of the wire which will not break
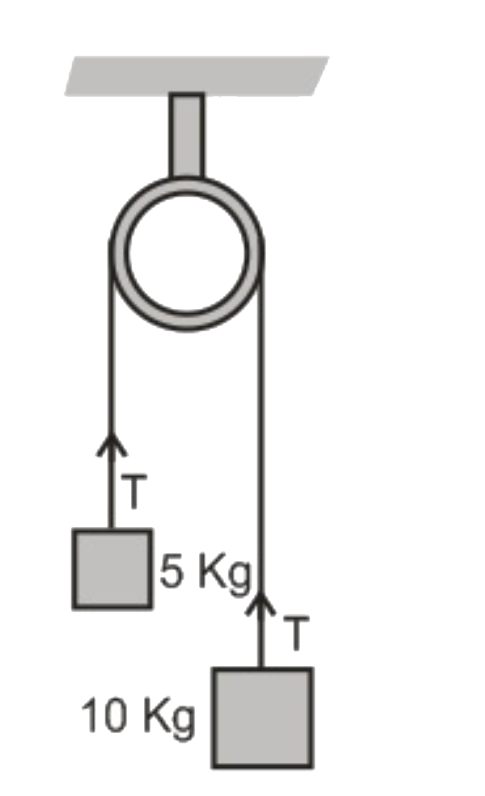
View SolutionOn a smooth table two blocks of masses 2.5kg and 1.5kg are placed one over the other as shown in figure. If the coefficient of static friction between two blocks is 0.2, the maximum horizontal force to be applied on the lower block so that the two blocks move together is (g = ms−2)
View SolutionTwo blocks of masses 1kg and 2kg are connected by a metal wire going over a smooth pulley as shown in figure.
The breaking stress of the metal is (40/3π)×106N/m2. If g=10ms−2, then what should be the minimum radius of the wire used if it is not to break?

View SolutionTwo masses 7 kg and 12 kg are connected at the two ends of a metal wire that goes ove a frictionless puulley. What should be in the minimum radius of the wire in order that the wire does not break,if the breaking stess of the metal is 1.3×108N/m2 ?
View SolutionTwo blocks of masses 40 kg and 20 kg are connected by a wire that has a linear mass density of 1g/m. These blocks are being pulled across horizontal frictionless floor by horizontal force F that is applied to 20 kg block. A transverse wave travels on the wave between the blocks with a speed of 400m/s (relative to the wire). the lmass of the wire is negligible compared to the mass of the blocks. the magnitude of F is
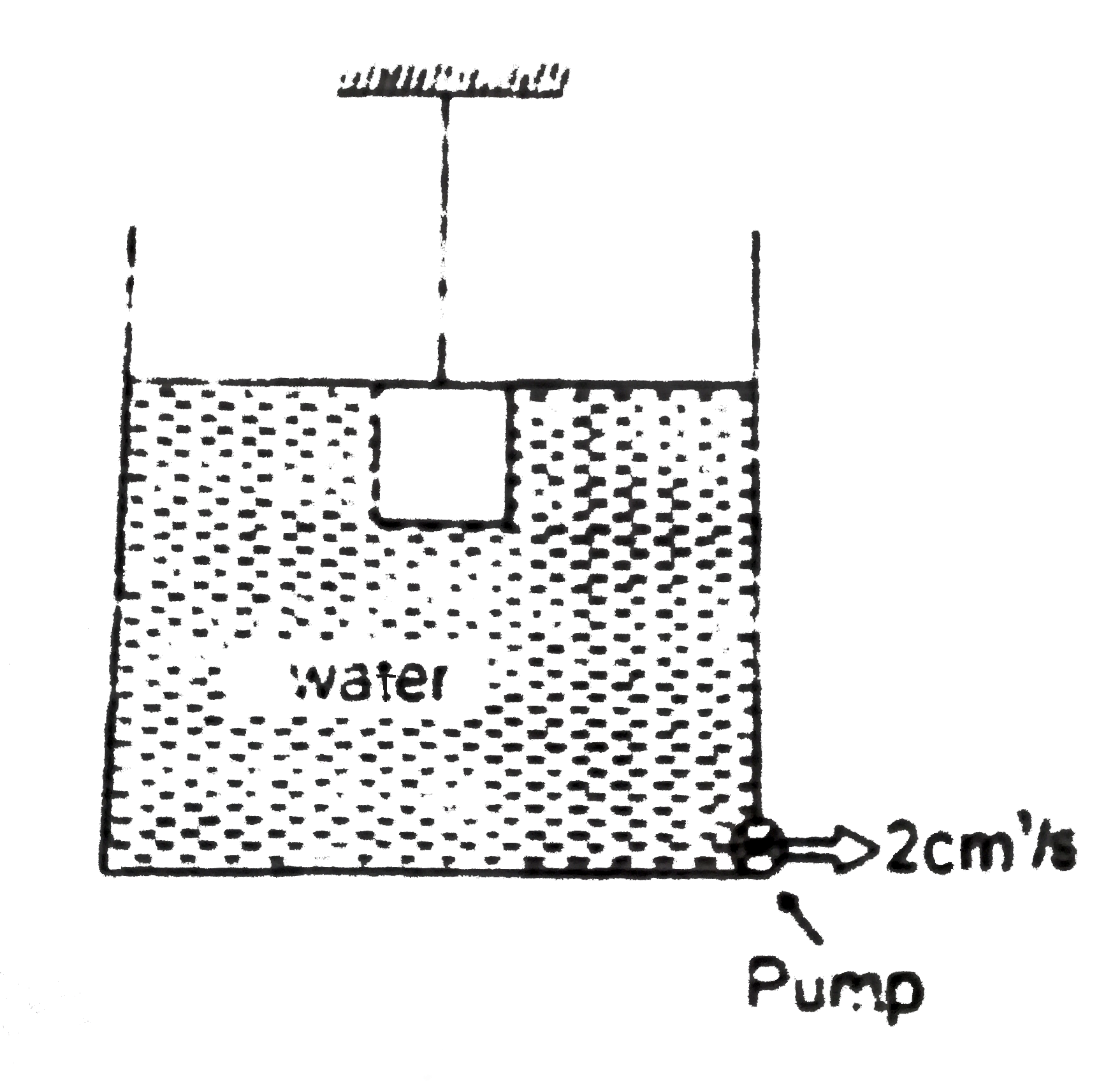
View SolutionFigure shows a cubical block of side 10 cm and relative density 1.5 suspended by a wire of cross sectional area 10−6m2. The breaking stress of the wire is 7×106N/m2. The block is placed in a beaker of base area 200cm2 and initially i.e. at t = 0, the top surface of water & the block coincide. There is a pump at the bottom corner which ejects 2cm3 of water per sec. Find the time at which the wire will break.
View Solution
