Two blocks of masses 40 kg and 20 kg are connected by a wire that has a linear mass density of 1g/m. These blocks are being pulled across horizontal frictionless floor by horizontal force F that is applied to 20 kg block. A transverse wave travels on the wave between the blocks with a speed of 400m/s (relative to the wire). the lmass of the wire is negligible compared to the mass of the blocks. the magnitude of F is
160 N
240 N
320 N
400 N
The correct Answer is:b
To solve the problem step by step, we will follow the reasoning laid out in the video transcript.
Step 1: Understand the System
We have two blocks of masses m1=40kg and m2=20kg connected by a wire with a linear mass density μ=1g/m=0.001kg/m. A force F is applied to the 20 kg block, and a transverse wave travels along the wire with a speed of v=400m/s.
Hint: Identify the masses and the properties of the wire to understand the system.
Step 2: Calculate the Total Mass
The total mass of the system is the sum of the masses of the two blocks:
mtotal=m1+m2=40kg+20kg=60kg
Hint: The total mass is essential for calculating the acceleration of the system.
Step 3: Relate Tension to Wave Speed
The speed of the wave in the wire is given by the formula:
v=√Tμ
where T is the tension in the wire. Rearranging this gives:
T=v2⋅μ
Hint: Use the wave speed formula to express tension in terms of wave speed and linear mass density.
Step 4: Substitute Known Values
Substituting the known values into the tension equation:
T=(400m/s)2⋅(0.001kg/m)=160N
Hint: Ensure units are consistent when performing calculations.
Step 5: Relate Tension to Force
The tension in the wire is also related to the force F applied to the 20 kg block. The tension is what pulls the 40 kg block. The acceleration a of the system can be expressed as:
a=Fmtotal=F60
The tension can also be expressed as:
T=m1⋅a=40⋅F60=2F3
Hint: Use Newton's second law to relate force, mass, and acceleration.
Step 6: Set Up the Equation
Now we have two expressions for tension:
1. T=160N
2. T=2F3
Setting these equal gives:
160=2F3
Hint: Equate the two expressions for tension to find the force.
Step 7: Solve for Force F
To find F, multiply both sides by 3:
480=2F
Now divide by 2:
F=240N
Hint: Isolate F to find its value.
Final Answer
The magnitude of the force F applied to the 20 kg block is:
240N
We have two blocks of masses m1=40kg and m2=20kg connected by a wire with a linear mass density μ=1g/m=0.001kg/m. A force F is applied to the 20 kg block, and a transverse wave travels along the wire with a speed of v=400m/s.
The total mass of the system is the sum of the masses of the two blocks:
mtotal=m1+m2=40kg+20kg=60kg
The speed of the wave in the wire is given by the formula:
v=√Tμ
where T is the tension in the wire. Rearranging this gives:
T=v2⋅μ
Substituting the known values into the tension equation:
T=(400m/s)2⋅(0.001kg/m)=160N
The tension in the wire is also related to the force F applied to the 20 kg block. The tension is what pulls the 40 kg block. The acceleration a of the system can be expressed as:
a=Fmtotal=F60
The tension can also be expressed as:
T=m1⋅a=40⋅F60=2F3
Now we have two expressions for tension:
1. T=160N
2. T=2F3
160=2F3
To find F, multiply both sides by 3:
480=2F
Now divide by 2:
F=240N
The magnitude of the force F applied to the 20 kg block is:
240N
Topper's Solved these Questions
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Single Correct Answer
1 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Multiple Correct
25 Videos
- TRAVELLING WAVESBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRAVELLING WAVESEXERCISE - Subjective
16 Videos
- TRANSMISSION OF HEATBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - TRANSMISSION OF HEATEXERCISE - Single correct
9 Videos
- VECTORSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - VECTORSEXERCISE - Exercise Multiple Correct
5 Videos
Similar Questions
A block of mass M is pulled along a horizontal frictionless surface by a rope of mass m . Force F is applied at one end of rope. The force which the rope exerts on the block is:
View SolutionTwo block of mass 1kg and 2kg are connected by a string AB of mass 1kg. The blocks are placed on a smooth horizontal surface. Block of mass 1kg is pulled by a horizontal force F of magnitude 8N. Find the tension in the string at points A and B

View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2Two blocks of masses 10 kg and 20 kg are connected by a massless string and are placed on a smooth horizontal surface as shown in the figure. If a force F=600 N is applied to 10 kg block, then the tension in the string is
 A100NB200NC300ND400N
A100NB200NC300ND400N
Two blocks of masses 2 kg and 1 kg are in contact with each other on a frictionless table. When a horizontal force of 3.0 N is applied to the block of mass 2 kg the value of the force of contact between the two blocks is:
View SolutionTwo blocks of masses 2 kg and 1 kg are in contact with each other on a frictionless table. When a horizontal force of 3.0 N is applied to the block of mass 2 kg the value of the force of contact between the two blocks is:
View SolutionTwo blocks of masses M1andM2 are placed in contact with each other on a frictionless horizontal surface. If a force F is applied on the block of mass M1, what is the contact force between the two blocks?
View SolutionTwo blocks of mass = 2 kg and M = 5 kg are in contact on a frictionless table. A horizonatal force F (= 35 N) is applies to m. Find the force of contact between the block, will the force of contact remain same if F is applied to M ?

View SolutionTwo blocks of masses 1 kg and 2 kg are placed in contact on a smooth horizontal surface as shown in fig. A horizontal force of 6N is applied d(a) on a 1-kg block. Find the force of interaction of the blocks.
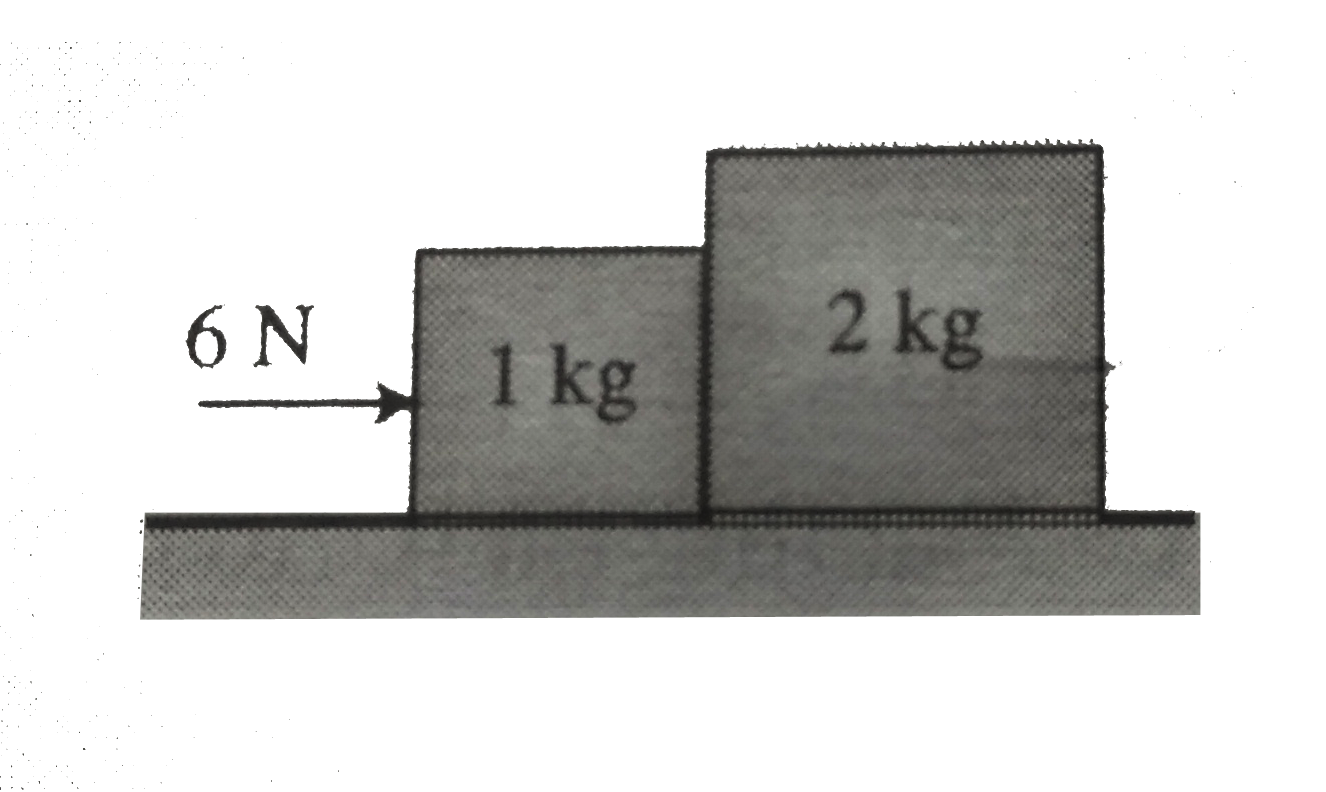
 .
.
View SolutionTwo blocks of masses 5kg and 2kg are connected by a spring of negligible mass and placed on a frictionless horizontal surface. An impulse provides a velocity of 7m/s to the heavier block in the direction of the lighter block. The velocity of the centre of mass is :-
View Solution
