Sounds from two identical sources S1 and S2 reach a point P. When the sounds reach directly, and in the same phase, the intensity at P is I0. The power of S1 is now reduced by 64% and the phase difference between S1 and S2 is varied continuously. The maximum and minimum intensities recorded at P are now Imax and Imin
Imax=0.64I0
Imin=0.36I0
ImaxImin=16
ImaxImin=1.640.36
The correct Answer is:A, C
To solve the problem, we need to determine the maximum and minimum intensities at point P when the power of source S1 is reduced by 64% and the phase difference between S1 and S2 is varied continuously.
1. Understanding Initial Conditions:
- When both sources S1 and S2 are in phase, the intensity at point P is given as I0.
- Since both sources are identical, we can denote their amplitudes as A.
2. Calculating Initial Intensity:
- The intensity I0 when both sources are in phase is given by:
I0=k(A+A)2=k(2A)2=4kA2
- Here, k is a constant that relates intensity to amplitude.
3. Power Reduction of Source S1:
- The power of S1 is reduced by 64%. Therefore, the remaining power is 36% of the original.
- Since power is proportional to the square of the amplitude, the new amplitude A′ of S1 can be calculated as:
A′=A√0.36=0.6A
4. New Amplitudes:
- The amplitude of S2 remains A.
- The new amplitudes are:
- For S1: A′=0.6A
- For S2: A=A
5. Calculating Maximum Intensity:
- The maximum intensity occurs when the waves from S1 and S2 are in phase. The resultant amplitude Amax is:
Amax=A+A′=A+0.6A=1.6A
- The maximum intensity Imax is then:
Imax=k(Amax)2=k(1.6A)2=2.56kA2
6. Calculating Minimum Intensity:
- The minimum intensity occurs when the waves from S1 and S2 are out of phase. The resultant amplitude Amin is:
Amin=A−A′=A−0.6A=0.4A
- The minimum intensity Imin is then:
Imin=k(Amin)2=k(0.4A)2=0.16kA2
7. Finding the Ratios:
- We can express Imax and Imin in terms of I0:
I0=4kA2
- Thus,
Imax=2.56kA2=2.564I0=0.64I0
Imin=0.16kA2=0.164I0=0.04I0
Final Results:
- The maximum intensity Imax=0.64I0
- The minimum intensity Imin=0.04I0
- When both sources S1 and S2 are in phase, the intensity at point P is given as I0.
- Since both sources are identical, we can denote their amplitudes as A.
- The intensity I0 when both sources are in phase is given by:
I0=k(A+A)2=k(2A)2=4kA2
- Here, k is a constant that relates intensity to amplitude.
- The power of S1 is reduced by 64%. Therefore, the remaining power is 36% of the original.
- Since power is proportional to the square of the amplitude, the new amplitude A′ of S1 can be calculated as:
A′=A√0.36=0.6A
- The amplitude of S2 remains A.
- The new amplitudes are:
- For S1: A′=0.6A
- For S2: A=A
- The maximum intensity occurs when the waves from S1 and S2 are in phase. The resultant amplitude Amax is:
Amax=A+A′=A+0.6A=1.6A
- The maximum intensity Imax is then:
Imax=k(Amax)2=k(1.6A)2=2.56kA2
- The minimum intensity occurs when the waves from S1 and S2 are out of phase. The resultant amplitude Amin is:
Amin=A−A′=A−0.6A=0.4A
- The minimum intensity Imin is then:
Imin=k(Amin)2=k(0.4A)2=0.16kA2
- We can express Imax and Imin in terms of I0:
I0=4kA2
- Thus,
Imax=2.56kA2=2.564I0=0.64I0
Imin=0.16kA2=0.164I0=0.04I0
- The maximum intensity Imax=0.64I0
- The minimum intensity Imin=0.04I0
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBook:ALLENChapter:WAVES AND OSCILLATIONSExercise:Part-1(Exercise-03)
Explore 31 Videos
- WAVES AND OSCILLATIONSBook:ALLENChapter:WAVES AND OSCILLATIONSExercise:Part-1(Exercise-04)[A]
Explore 29 Videos
- WAVES AND OSCILLATIONSBook:ALLENChapter:WAVES AND OSCILLATIONSExercise:Part-1(Exercise-01)
Explore 53 Videos
- SEMICONDUCTORSBook:ALLENChapter:SEMICONDUCTORSExercise:Part-3(Exercise-4)
Explore 51 Videos
Similar Questions
Two identical sources of sound S1andS2 produce intensity I0 at a point P equidistant from each source .
(i) Determine the intensity of each at the point P.
(ii) If the power of S1 is reduced to 64% and phase difference between the two sources is varied continuously , then determine the maximum and minimum intensities at the point P.
(iii) If the power of S1 is reduced by 64% , then determine the maximum and minimum intensities at the point P.
View SolutionTwo identical sounds s1ands2 reach at a point P phase. The resultant loudness at a point P is not higher than the loudness of s1. The value of n is
View Solution
Knowledge Check
In the case of light waves from two coherent sources S1 and S2, there will be constructive interference at an arbitrary point P, the path difference S1P−S2P is
A(n+12)λBnλC(n−12)λDλ2
The ratio of intensities between two coherent sound sources is 4:1 the difference of loudness in decibels between maximum and minimum intensities, when they interfere in space, is
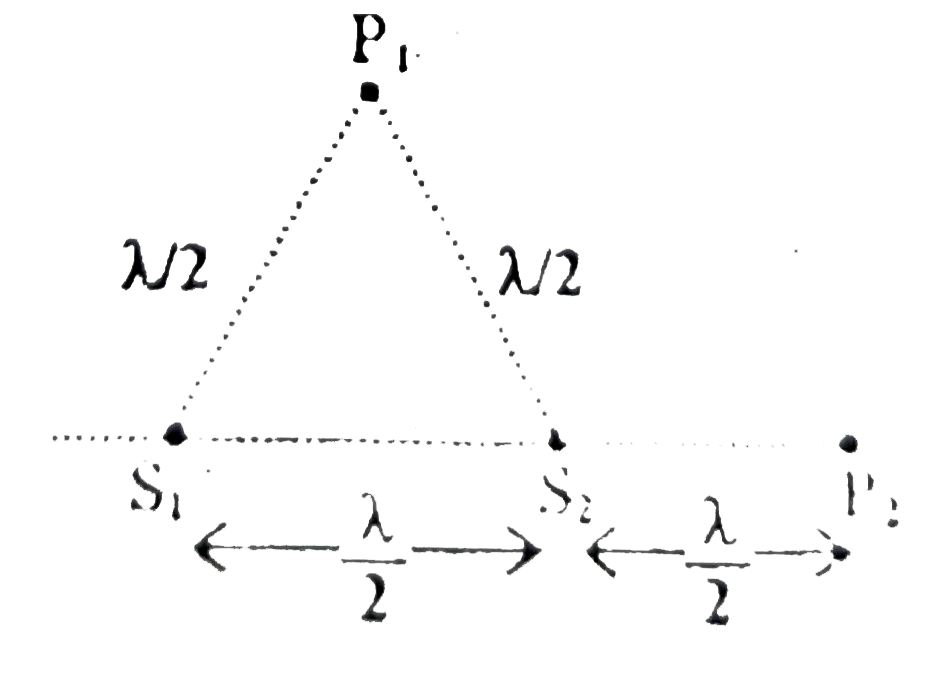
View SolutionS1 and S2 are two equally intense coherent point second sources vibrating in phase. The resultant intensity at P1 is 80SI units then resultant intensity at P2 in SI units will be
View SolutionIf the intensities of the two interfering beams in Young.s double -Slit experiment be I1 and I2 then the contrast between the maximum and minimum intensity is good when
View SolutionThe wavelength of sound waves arriving at P from two coherent sources S1 and S2 is 4 m as shown. While intensity of each wave is I0 the resultant intensity at point P is 2I0 find minimum value of x
_PHY_E06_238_Q01.png)
View SolutionS1 and S2 are two sources of sound emitting sine waves. The two sources are in phase. The sound emitted by the two sources interfers at point F. The waves of wavelength :

View Solution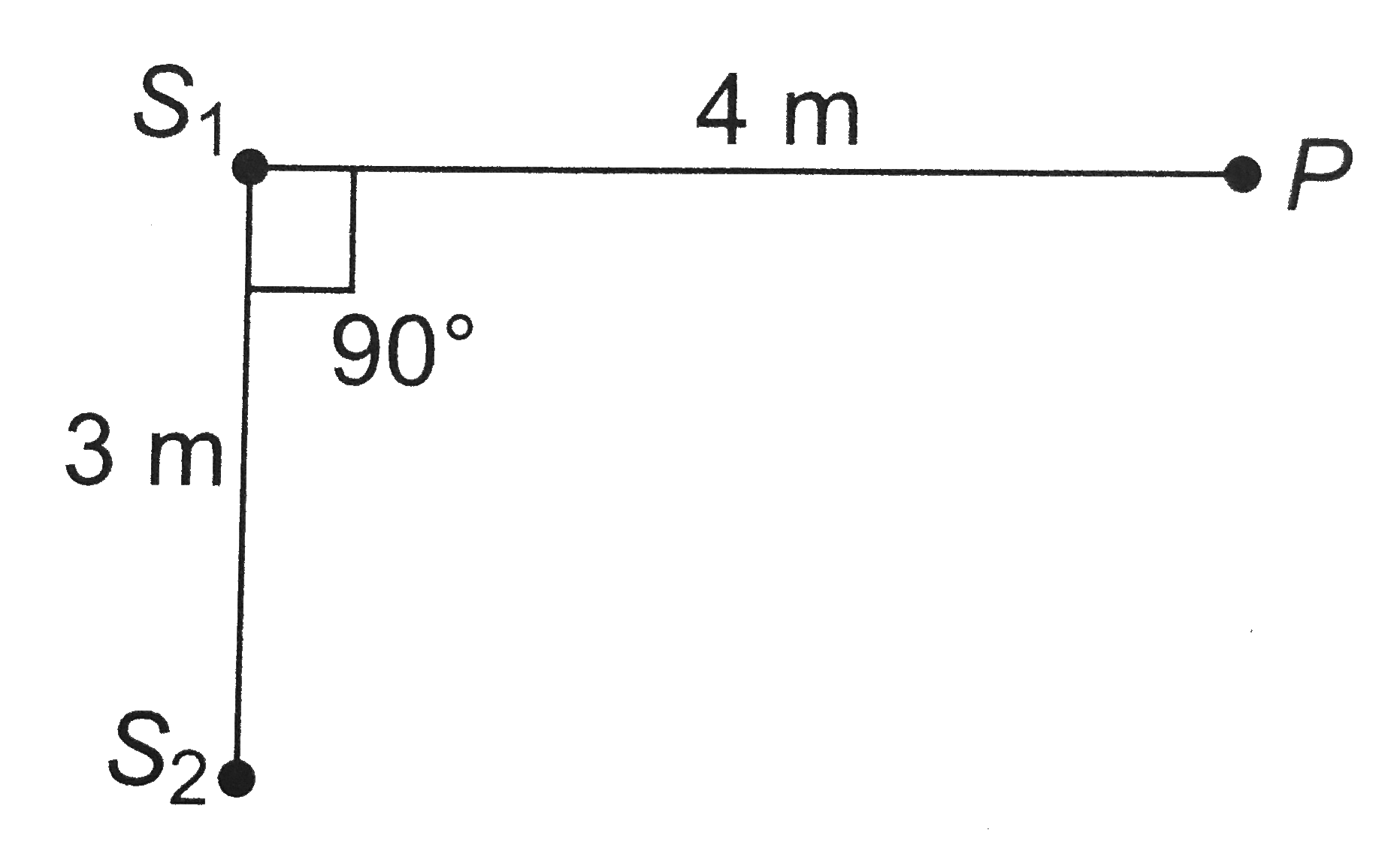
S1 and S2 are two coherent sources of sound of frequency 110Hz each they have no initial phase difference. The intensity at a point P due to S1 is I0 and due to S2 is 4I0. If the velocity of sound is 330m/s then the resultant intensity at P is
View SolutionAmong two interfering sources, let S1 be ahead of the phase by 90∘ relative to S2 . If an observation point P is such that PS1−PS2=1.5λ , the phase difference between the waves from S1andS2 reaching P is
View Solution