A vessel ABCD of 10 cm width has two small slits S1 and S2 sealed with identical glass plates of equal thickness. The distance between the slits is 0.8 mm. POQ is the line peropendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S, 40 cm below P and 2 m form the vessel to illuminate the slits as shown in figure .Calculate the position of the central bright fringe on the other wall CD with respect to line OQ. Now , a liquid is poured into the vessel and filled up to OQ. The central bright fringe is found to be at Q. Calculate the refractive index of the liquid to the liquid.
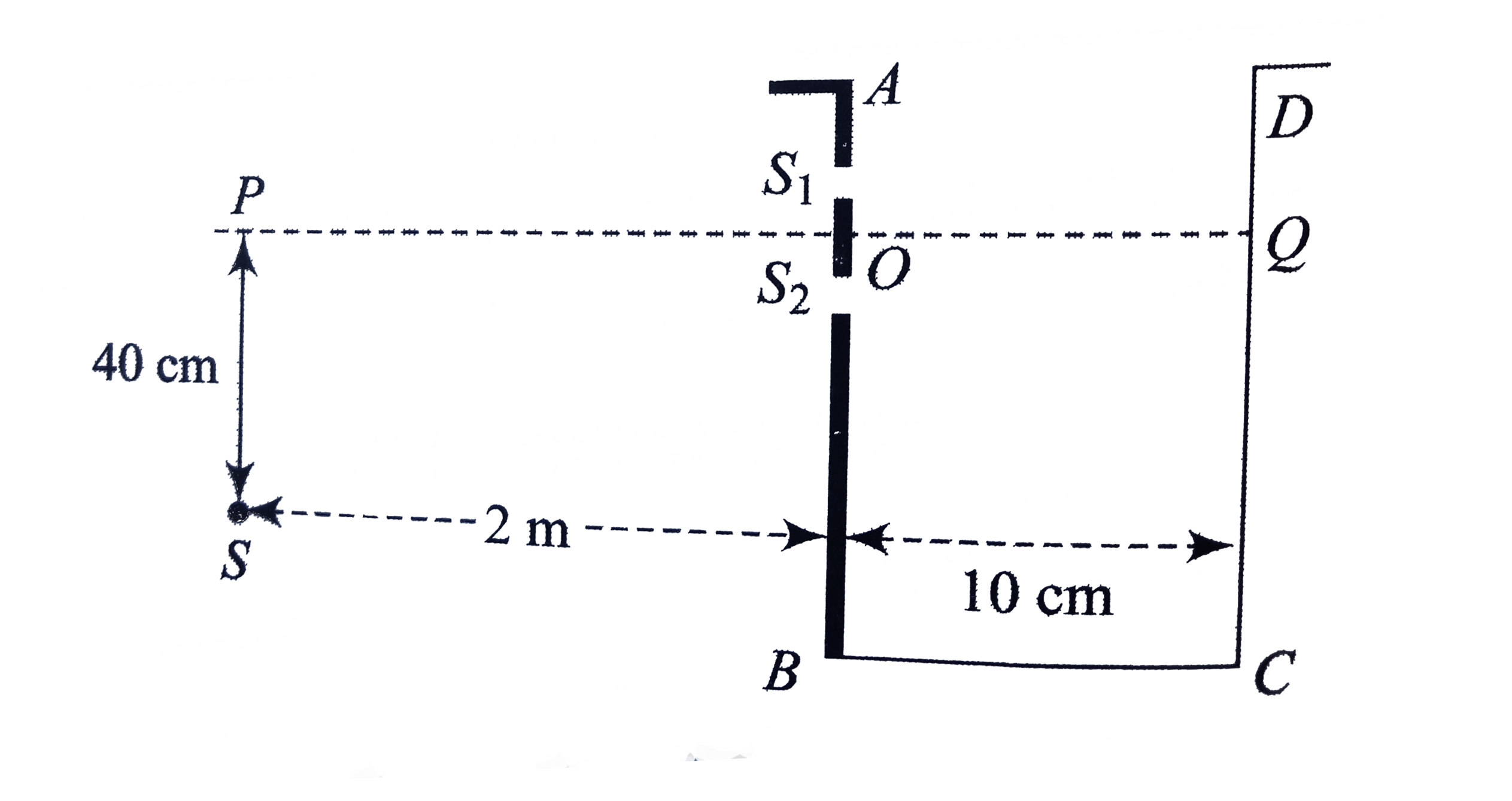
The correct Answer is:2 cm above point Q on side CD,μ=1.0016
_E01_140_S01.png)
(i) O is the middle point of slits S1&S2 also S1S2=d=0.8mm in figure tanα=y1D1
tanα=40200=15∴sinα=1√26=15.1≈15≈tanα
path difference Δx1=SS1−SS2
Δx1=dsinα=0.8×15 or Δx1=0.16mm ...(i)
let R represents the position of CBF. i.e.,
net path difference should be 0
Now Δx2=S2R−S1R
or Δx2=dsinθ⇒Δx1=Δx2 ..(ii)
For central bright fringe
Δx2−Δx1=0⇒dsinθ−Δx1=0
⇒dsinθ=Δx1=0.16mm
⇒(0.8)sinθ=0.16⇒sinθ=0.160.8=15
∴tanθ=1√24=14.9=15=sinθ
So, tanθ=y2D2=15⇒y2=2cm
(ii). _E01_140_S02.png)
When liquid of refractive index μ is poured
Then for CBF at Q, net path difference =0
(μ−1)t=Δx1⇒(μ−1)100=0.16⇒μ−1=0.0016
Topper's Solved these Questions
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)
7 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 5 A (Previous Years Questions)
17 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A vessel ABCD of 10cm width has two small slits S1 and S2 sealed with idebtical glass plates of equal thickness. The distance between the slits is 0.8mm. POQ is the line perpendicular to the plane AB and passing through O, the middle point of S1 and S2. A monochromatic light source is kept at S,40cm below P and 2m from the vessel, to illuminate the slits as shown in the figure. Calculate the position of the central bright fringe on the other wall CD with respect of the line OQ. Now, a liquid is poured into the vessel and filled up to OQ. The central bright fringe is fiund to be at Q. Calculate the refractive index of the liquid.

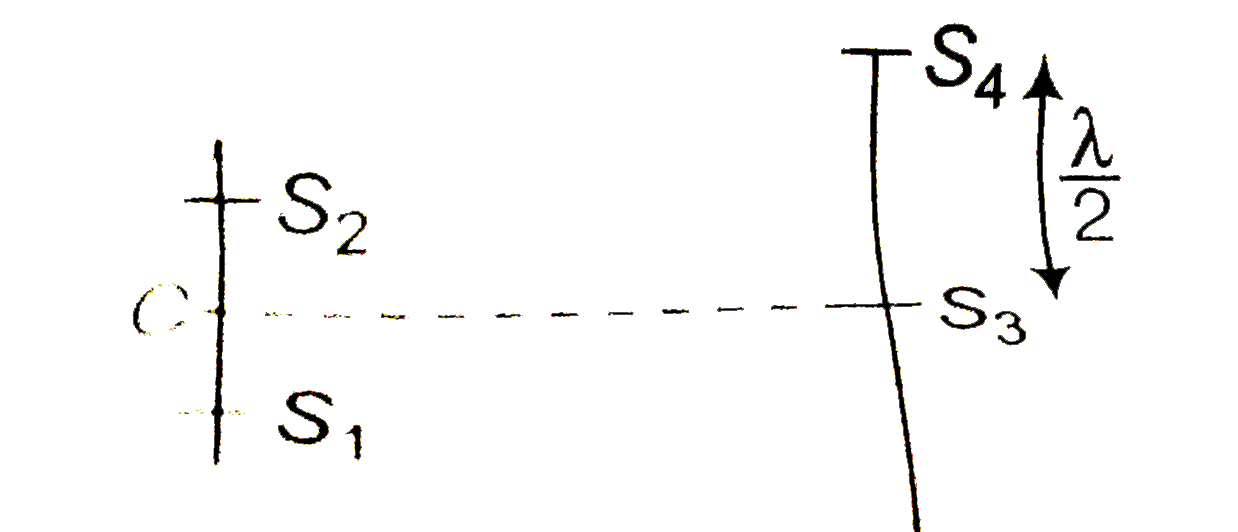
View SolutionIn the given figure ,C is middle point of line S1S2.A monochromatic light of wavelength γ is incident on slits.The ratio of intensites of S3andS4 is
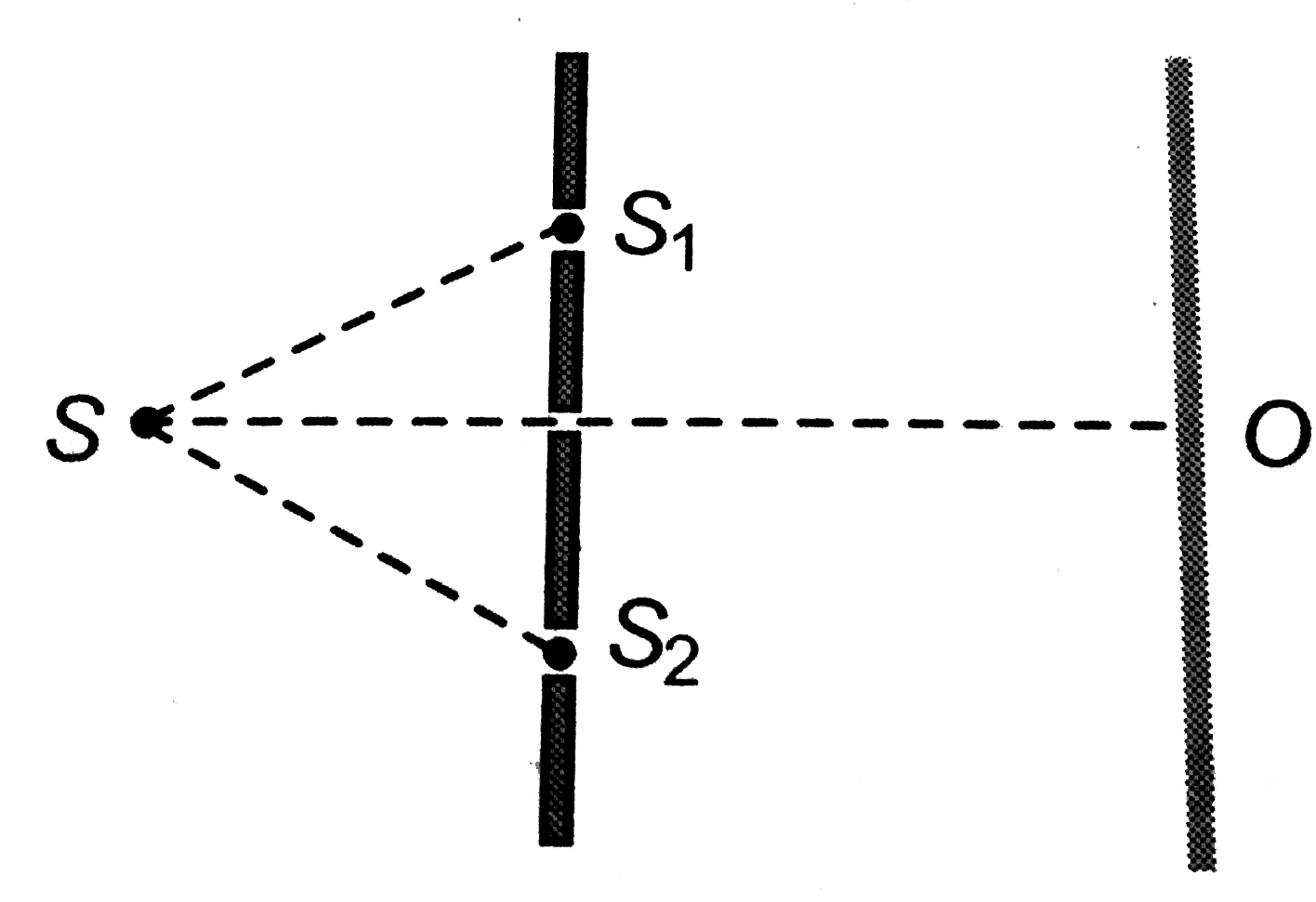
View SolutionIn the set up shown in figure, the two slits S1 and S2 are not equidistant from the slit S. The central fringe at O is then
View SolutionS1 and S2 are two coherent sources of sound having no intial phase difference. The velocity of sound is 330m/s. No maximum will be formed on the line passing through S2 and prependicular to the line joining S1 and S2. If the frequency of both the sources is
View SolutionTwo point sources S1 and S2 are 24 cm apart. What should a convex lens of focal length 9 cm be placed between them so that the images of both sources formed at the same place ?
View SolutionIn a young 's double slit experiment, a glass plate of refractive index 1.5 and thickness 5×10−4 cm is kept in the path of one of the light rays. Then
View SolutionIn the figure shown S is the saurce of white light kept at a distance x0 frorn the plane of the slits. The source moves with a constant specd u towards the slits on the line perpendicular to the plane of the slits and passing through the slit S1. Find the instanteneous velocity (magnituce and direction). of the central maxima at time t having range 0≤t<<x0−du. Assume that D>>d.

View SolutionTwo coherent sources S1 and S2 are separated by a small distance d. The fringes obtained on the screen will be:
View Solution_S01_026_Q01.png)
In a YDSE experiment two slits S1 and S2 have separation of d=2mm the distance of the screen is D=85 m source S starts moving from a very large distance towards S2 perpendicular to S1S2 as shown in figure the wavelength of monochromatic light is 500 nm. The number of maximas observed on the screen at point P as the moves towards S2 is
View SolutionTwo coherent point sources S1 and S2 vibrating in phase light of wavelength λ. The separation between the sources is 2λ. The smallest distance from S2 on a line passing through S2 and perpendicular to s1s2 where a minimum of intensity occurs is
View Solution
