A glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer and two reflected rays interfere. Write the condition for their constructive interfere. If the λ=648nm, obtain the least value of t for which the rays interfere constrcutively.
The correct Answer is:2μt=(n−12)λ with μ=1.8 and n=1,2,3..90,tmin=90nm
_E01_139_S01.png)
AB denotes incident ray. It is partly reflected from the upper surface of layer as R1.R1 is reflected from a denser medioum. It undergoes a phase change of π. Part of AB is relfected from surface of layer as R2.R2 is reflected from a rares medium
as .aμm=1.8 and .aμg=1.5
R1 and R2 therefore passess an initial phase difference of π before they undergo interference net phase ddifference should be 2nπ where n is an integer.
Δϕ=2nπ−π(2n−1)π∴x=(2n−1)λ2
since Δx=2(μm)t=1.8×2t=3.6t
or 3.6t=(2n−1)λ2
For least value of t is n=1∴3.6×tminλ2
or tmin=6483.6×2nm or tmin=90nm.
Topper's Solved these Questions
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 2 (Previous Year Questions)
Explore 7 Videos
- WAVE OPTICSBook:ALLENChapter:WAVE OPTICSExercise:Exercise 5 A (Previous Years Questions)
Explore 17 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Book:ALLENChapter:UNIT & DIMENSIONS, BASIC MATHS AND VECTOR Exercise:Exercise (J-A)
Explore 7 Videos
Similar Questions
A glass of refractive index 1.5 is coated with a thin layer of thickness t and refractive index 1.8 . Light of wavelength λ travelling in air is incident normally on the layer. It is partly reflected at the upper and the lower surfaces of the layer. It is partly reflected at the upper and the lower surfaces of the layer ant the two reflected rays interface . If λ=648nm, obtain the least value of t(in10−8m) which the rays interface constructively.
View SolutionThe outer surface of a transparent glass slab of refractive index μS=1.5 is coated by a thin layer of transparent medium of refractive index μC=1.6. Orange light of wavelength 6400Å falls normally on the coating. The reflected light at the upper surface and at the lower surface of the coat interfere destructively. If thickness of the coat is 5K×10−8m, calculate the minimum value of K.
View SolutionA glass prism of refractive index 1.5 is immersed in water of refractive index 4/3. A light ray incident normally on face AB is totally reflected at face AC if
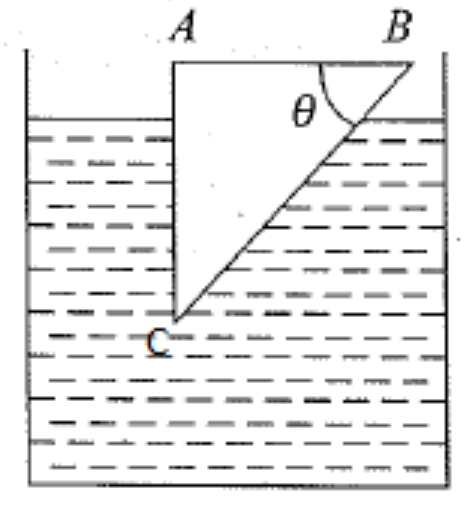
View SolutionWhite light is incident normally on a glass plate (in air) of thickness 500nm and refractive index of 1.5. The wavelength (in nm) in the visible region (400nm−700nm) that is strongly reflected by the plate is:
View SolutionA glass prism of refractive index 1.5 is immersed in water (refractive index 4/3) . A light beam normally on the face AB is totally reflected to reach on the face BC if

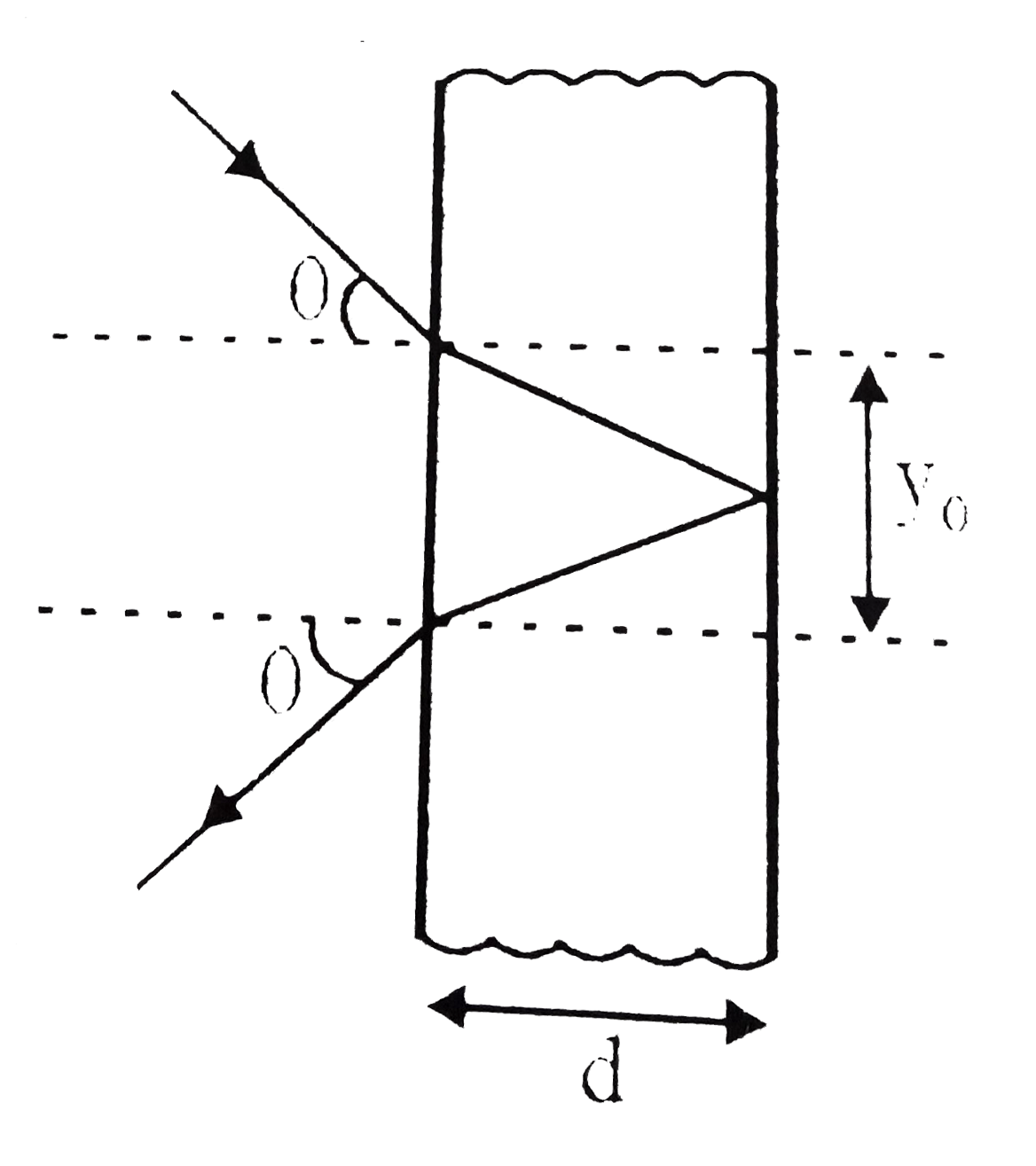
View SolutionA ray of light incident from air on a glass plate of refractive index n is partly reflected and partly refracted at the two surfaces of the glass. The displacement y0 in the figure is
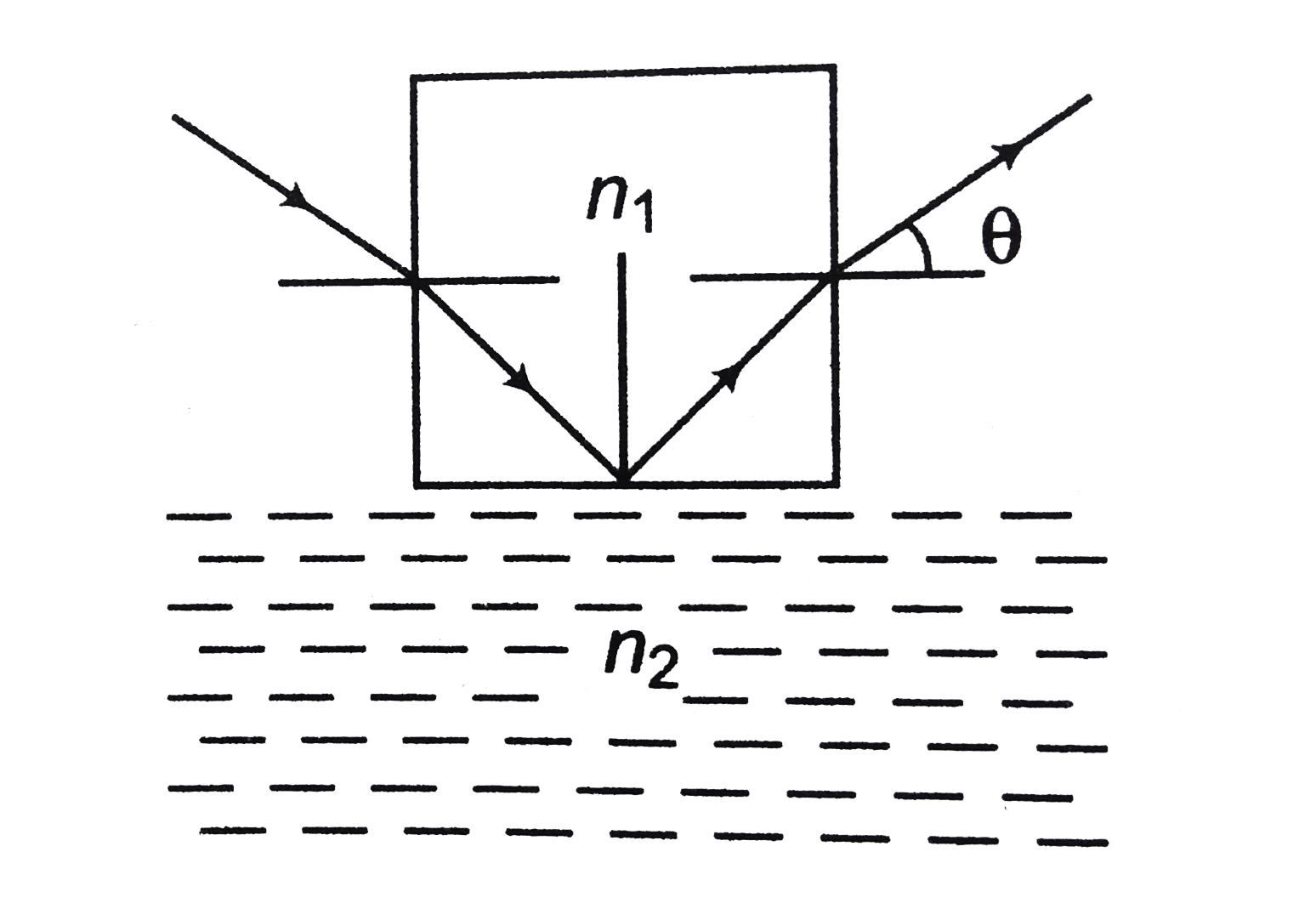
View SolutionA cubical block of glass of refractive index n1 is in contact with the surface of water of refractive index n2. A beam of light is incident on vertical face of the block. After refraction a total internal reflection at the base and refraction at the opposite face take place. The ray emerges at angle θ as shown. The value of θ is given by
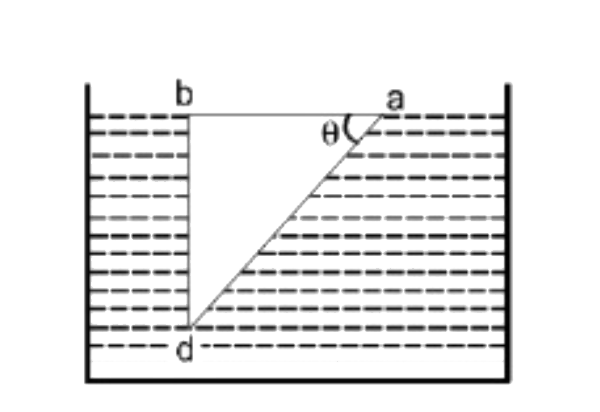
View SolutionA glass prism is immeresed in water as shown in the figure. When a beam of light incident is incident normally on the face ab, it is internally reflected at the face ad. If the refractive index of glass is 1.5 and that of water is 4/3, then
View SolutionA ray of light entering from air to glas (μ=1.5) is partly reflected and partly refracted. lf the reflected and refracted rays are at right angles to each other, the angle of refraction is
View SolutionWhen a ray of light is incident normally on one refracting surface of an equilateral prism (Refractive index of the material of the prism =1.5
View Solution

