To make the central fringe at the centre O, a mica sheet of refractive index 1.5 is introduced . Choose the correct statement(s). (D>>d>>λ)
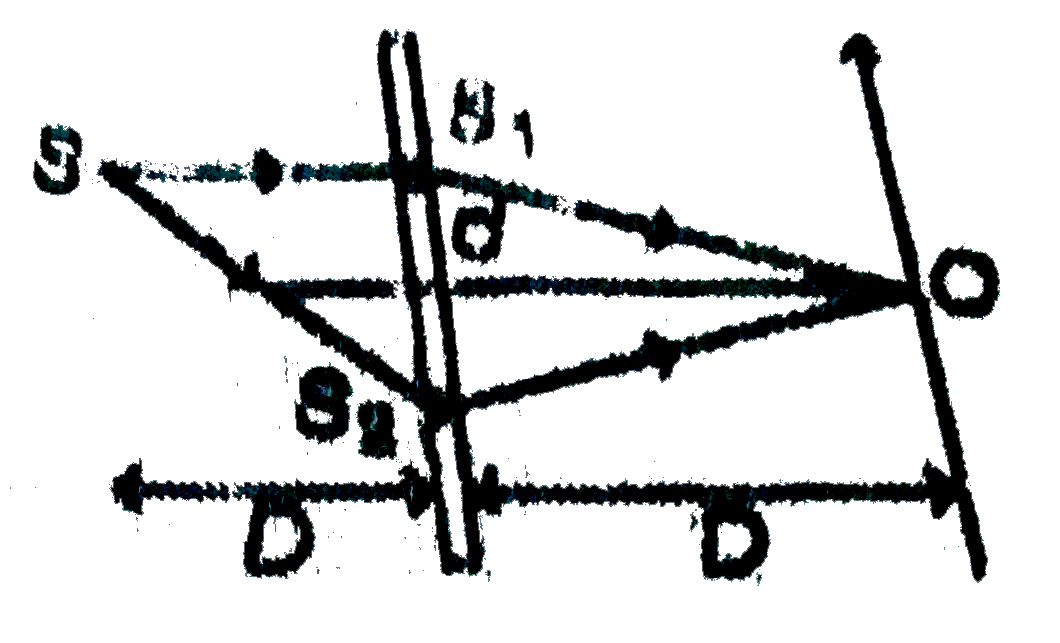
the thickness of sheet is 2(√2−1)d infront of S1
the thickness of sheet is (√2−1)d infront of S2
the thickness of sheet is 2√2d infront of S1
the thickness of sheet is (2√2−1)d infront S1.
The correct Answer is:A
Here the shift produced by mica sheet of thickness t is (μt−t)=t(μ−1). It should be equal to extra path traveled by the ray SS2O i.e., Δ=SS2−d=√2d−d
⇒t2=d(√2−1)⇒t=2d(√2−1) infront of S1
Topper's Solved these Questions
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 3 (Miscellaneous type Questions)
27 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 4 A (Conceptual subjective Exercise)
9 Videos
- WAVE OPTICSBOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 1 (Check your Grasp)
75 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
To make the central fringe at the centerO , mica sheet of refractive index 1.5 is introduced Choose the corect statement.
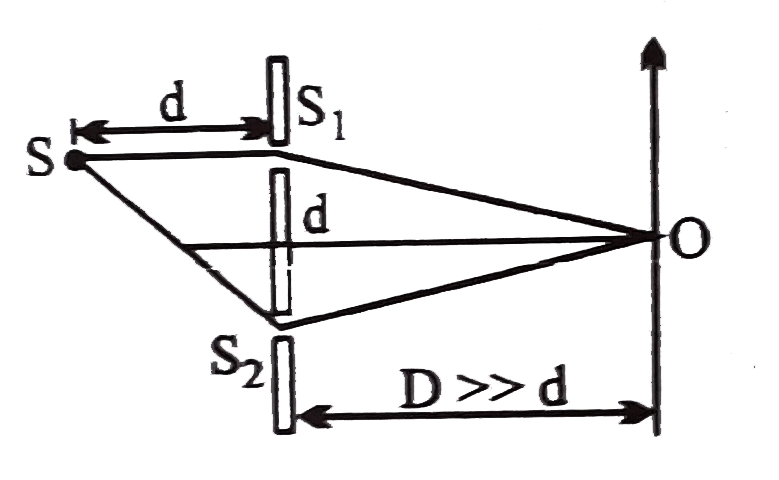
View SolutionTo make the central fringe at the center O , a mica - sheet index 1.5 is introduced .Choose the correct statement (s)
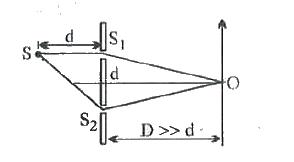
View SolutionThe central fringe of the interference pattern produced by the light of wavelength 6000 Å is found to shift to the position of 4th dark fringe after a glass sheet of refractive index 1.5 is introduced. The thickness of glass sheet would be
View SolutionIn YDSE using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.5 and thickness 2 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the plane of slits and the screen is doubled. It is found that the distance between successive maxima (or minima) now is the same as the observed fringe shift upon the introduction of the mica sheet. Calculate the wavelength of the light.
View SolutionIn a Young's double slit experiment using monochromatic light, the fringe pattern shifts by a certain distance on the screen when a mica sheet of refractive index 1.6 and thickness 1.964 microns is introduced in the path of one of the interfering waves. The mica sheet is then removed and the distance between the slits and screen is doubled. It is found that the distance between successive maxima now is the same as observed fringe shift upon the introduced of the mica sheet . Calculate the wavelength of the monochromatic light used in the experiment .
View SolutionA thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
View SolutionA thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
View SolutionA thin mica sheet of thickness 2×10−6m and refractive index (μ=1.5) is introduced in the path of the first wave. The wavelength of the wave used is 5000Å. The central bright maximum will shift
View SolutionConsider the optical system shown in figure. The point source of ligth S is having wavelength equal to λ. The light is reaching screen only after reflection. For point P to be socond maxima, the value of λ would be (D>>d and d>>λ)
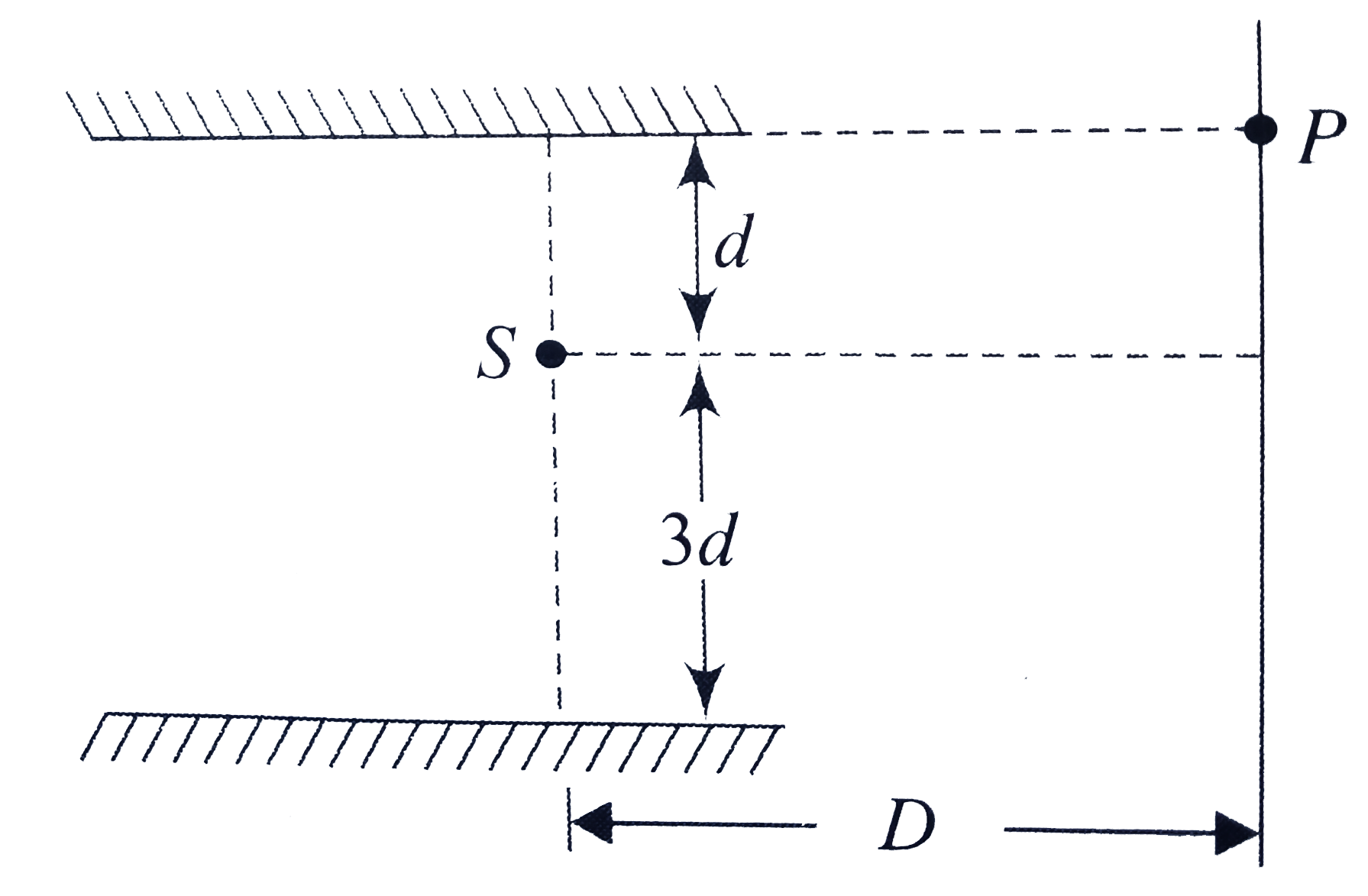
View SolutionConsider the optical system shown in figure. The point source of ligth S is having wavelength equal to λ. The light is reaching screen only after reflection. For point P to be socond maxima, the value of λ would be (D>>d and d>>λ)

View Solution
