A man of mass m starts falling towards a planet of mass M and radius R. As he reaches near to the surface realizes that he will pass through a small hole in the planet. As he enters the hole he seen that the planet really made of two places a spherical shell of negligible thickness of mass 2M3 and a point mass M3 of centre. Change in the force of gravity experienced by the man is
23GMR2
0
13GMmR2
43GMmR2
The correct Answer is:A
To solve the problem of the change in gravitational force experienced by a man falling towards a planet with a specific structure, we can follow these steps:
1. Understanding the Structure of the Planet:
The planet consists of two parts:
- A spherical shell with mass 2M3
- A point mass at the center with mass M3
2. Gravitational Field Inside the Shell:
According to the shell theorem, the gravitational field inside a spherical shell of uniform density is zero. Therefore, when the man is inside the shell, he experiences no gravitational force from the shell.
Eshell=0
3. Gravitational Force Due to the Point Mass:
When the man is at a distance r from the center of the planet, the only gravitational force acting on him is due to the point mass at the center. The gravitational force Fnew can be calculated using Newton's law of gravitation:
Fnew=G⋅(M3)⋅mr2
4. Gravitational Force Near the Surface:
When the man is outside the shell, the gravitational force Fold he experiences is due to the total mass of the planet:
Fold=G⋅M⋅mR2
5. Change in Gravitational Force:
The change in gravitational force experienced by the man as he passes from outside the shell to inside the shell can be calculated as:
ΔF=Fold−Fnew
Substituting the expressions for Fold and Fnew:
ΔF=G⋅M⋅mR2−G⋅(M3)⋅mr2
6. Simplifying the Expression:
To simplify, we can factor out G⋅m:
ΔF=G⋅m(MR2−M3r2)
Assuming r approaches R as the man reaches the surface:
ΔF=G⋅m(MR2−M3R2)
This simplifies to:
ΔF=G⋅m⋅2M3R2
7. Final Result:
Thus, the change in gravitational force experienced by the man is:
ΔF=2GmM3R2
The planet consists of two parts:
- A spherical shell with mass 2M3
- A point mass at the center with mass M3
According to the shell theorem, the gravitational field inside a spherical shell of uniform density is zero. Therefore, when the man is inside the shell, he experiences no gravitational force from the shell.
When the man is at a distance r from the center of the planet, the only gravitational force acting on him is due to the point mass at the center. The gravitational force Fnew can be calculated using Newton's law of gravitation:
When the man is outside the shell, the gravitational force Fold he experiences is due to the total mass of the planet:
The change in gravitational force experienced by the man as he passes from outside the shell to inside the shell can be calculated as:
To simplify, we can factor out G⋅m:
Thus, the change in gravitational force experienced by the man is:
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 2 (Brain Teasers)
27 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - Exercise 3 (Miscellaneous Type Questions)
20 Videos
- GRAVITATIONBOOK - ALLENCHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
- GEOMETRICAL OPTICSBOOK - ALLENCHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLENCHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
46 Videos
Similar Questions
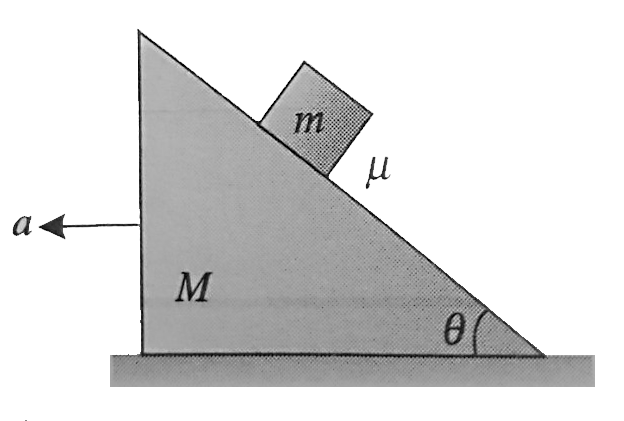
A block of mass m is at rest relative to the stationary wedge of mass M. The coefficient of friction between block and wedge is μ. The wedge is now pulled horizontally with acceleration a as shown in figure. Then the minimum magnitude of a for the friction between block and wedge to be zero is:
View SolutionA thin spherical shell of mass M and radius R has a small hole. A particle of mass m released at its mouth. Then
View Solution
Knowledge Check
A point mass m is placed inside a spherical shell of radius R and mass M at a distance R2 form the centre of the shell. The gravitational force exerted by the shell on the point mass is
AGMmR2B2GMmR2CzeroD4MmR2A particle of mass m is placed at the centre of a unifrom spherical shell of mass 3 m and radius R The gravitational potential on the surface of the shell is .
AGMRB−GMRC−4GMRD−2GMRA mass m is placed at point P lies on the axis of a ring of mass M and radius R at a distance R from its centre. The gravitational force on mass m is
AGMm√2R2BGMm2R2CGMm2√2R2DGMm4R2
A body of mass m at inifnity is approaching the centre of a hypothetical hollow planet of mass M and radius R. The speed of the body when it passes the centre of the planet through a diametrical tunnel is
View SolutionA small hole is made in a disc of mass M and radius R at a distance R/4 from centre. The disc is supported on a horizontal peg through this hole. The moment of inertia of the disc about horizontal peg is
View SolutionThe mass of a planet is twice the mass of earth and diameter of the planet is thrie the diameter of the earth, then the acceleration due to gravity on the planet's surface is
View SolutionA body of mass m is placed at the centre of the spherical shell of radius R and mass M. The gravitation potential on the surface of the shell is
View SolutionA spherical planet far out in space has mass 2M and radius a. A particle of mass m is falling freely near its surface. What will be the acceleration of that particle ?
View Solution
