A cylindrical vessel filled with water up to a height of 2m stands on a horizontal plane. The side wall of the vessel is a plugged circular hole touching the bottom. Find the minimum diameter of the hole so that the vessel begins to move on the floor if the plug is removed. The coefficient of friction between the bottom of the vessel and the plane is 0.4 and the total mass of water plus vessel is 100 kg.
To solve the problem step by step, we need to analyze the forces acting on the cylindrical vessel when the plug is removed.
Step 1: Determine the velocity of the water exiting the hole
The velocity V of the water flowing out of the hole can be calculated using Torricelli's theorem:
V=√2gh
where g is the acceleration due to gravity (approximately 9.81m/s2) and h is the height of the water column (which is 2m).
Step 2: Calculate the force due to the exiting water
The force F exerted by the exiting water can be calculated using the rate of momentum imparted to the vessel:
F=ρAV
Substituting V from Step 1, we have:
F=ρA√2gh
where A is the area of the hole and ρ is the density of water (approximately 1000kg/m3).
Step 3: Set the force of water equal to the force of friction
The vessel will begin to move when the force due to the exiting water equals the force of friction Ff:
F=μmg
where μ is the coefficient of friction (given as 0.4), m is the total mass of water plus the vessel (given as 100kg), and g is the acceleration due to gravity.
Step 4: Substitute and rearrange the equations
Equating the two forces:
ρA√2gh=μmg
Substituting the known values:
1000A√2×9.81×2=0.4×100×9.81
Step 5: Calculate the area A
Now we can solve for A:
1000A√39.24=392.4
1000A×6.26=392.4
A=392.46260≈0.0627m2
Step 6: Relate area to diameter
The area A of the hole can be expressed in terms of the diameter D:
A=πD24
Setting the two expressions for A equal:
πD24=0.0627
Step 7: Solve for diameter D
Rearranging gives:
D2=0.0627×4π
D2=0.25083.14159≈0.0798
D≈√0.0798≈0.2827m≈0.283m
Final Answer
Thus, the minimum diameter of the hole so that the vessel begins to move on the floor is approximately 0.283m or 28.3cm.
---
The velocity V of the water flowing out of the hole can be calculated using Torricelli's theorem:
V=√2gh
where g is the acceleration due to gravity (approximately 9.81m/s2) and h is the height of the water column (which is 2m).
The force F exerted by the exiting water can be calculated using the rate of momentum imparted to the vessel:
F=ρAV
Substituting V from Step 1, we have:
F=ρA√2gh
where A is the area of the hole and ρ is the density of water (approximately 1000kg/m3).
The vessel will begin to move when the force due to the exiting water equals the force of friction Ff:
F=μmg
where μ is the coefficient of friction (given as 0.4), m is the total mass of water plus the vessel (given as 100kg), and g is the acceleration due to gravity.
Equating the two forces:
ρA√2gh=μmg
Substituting the known values:
1000A√2×9.81×2=0.4×100×9.81
Now we can solve for A:
1000A√39.24=392.4
1000A×6.26=392.4
A=392.46260≈0.0627m2
The area A of the hole can be expressed in terms of the diameter D:
A=πD24
Setting the two expressions for A equal:
πD24=0.0627
Rearranging gives:
D2=0.0627×4π
D2=0.25083.14159≈0.0798
D≈√0.0798≈0.2827m≈0.283m
Thus, the minimum diameter of the hole so that the vessel begins to move on the floor is approximately 0.283m or 28.3cm.
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Elasticity)
16 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLENCHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)
21 Videos
- CENTRE OF MASSBOOK - ALLENCHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLENCHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
For the arrangement shown in the figure, the force at the bottom of the vessel is
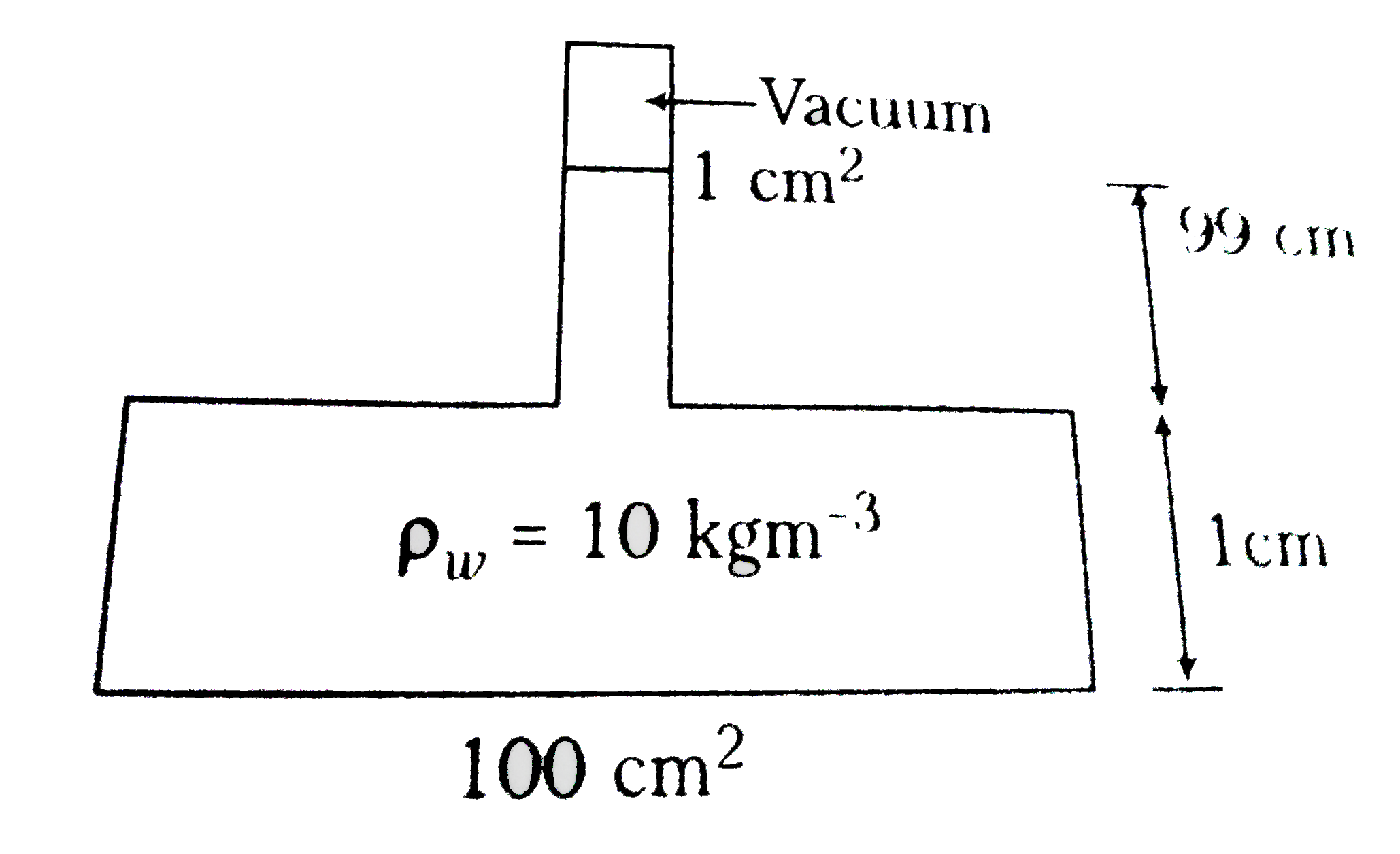
View SolutionA cylindrical vessel is filled with a liquid up to a height H. A small hole is made in the vessel at a distance y below the liquid surface as shown in figure. The liquid emerging from the hole strike the ground at distance x
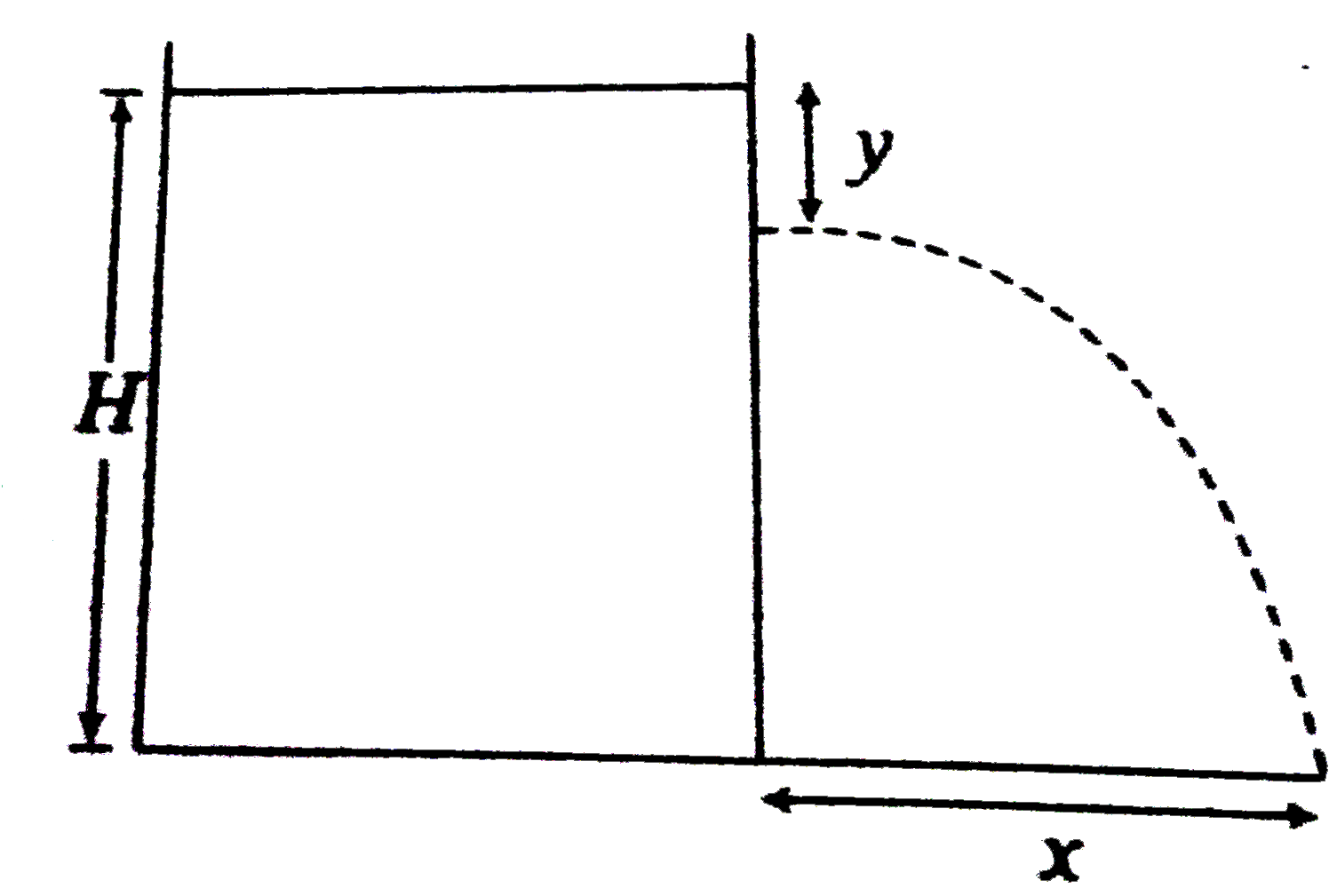
View SolutionA large cylindrical vessel contains water to a height of 10 m. If is found that the thrust acting on the curved surface is equal to that at the bottom. If atmospheric pressure can support a water column of 10 m. the radius of the vessel is
View SolutionA cylindrical vessel of area of cross section A is filled with a liquid up to a height H. A very small hole of area of cross section a is made at the bottom of the vellel. Find the time taken by the vessel to become empty.
View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylindrical vessel contains a liquid of density ρ up to height h. The liquid is closed by a piston of mass m and area of cross section A. There is a small hole at the bottom of the vessel. The speed v with which the liquid comes out of the hole is

View SolutionA cylindrical vessel having diameter equal to its height is full of water which is poured into two identical cylindrical vessels with diameter 42 cm and height 21 cm which are filled completely. Find the diameter of the cylindrical vessel.
View SolutionA closed vessel is half filled with water. There is a hole near the top of vessel and air is pumped out from this hole.
View SolutionOn the opposite sides of vertical vessel filled with water, two identical holes are opened. If area of cross-section for each is a and difference of height of these two is h and p is density of water, then force on the vessel is
View SolutionAn open cylindrical vessel of internal diameter 7 cm and height 8 cm stands on a horizontal table. Inside this is placed a solid metallic right circular cone, the diameter of whose base is 312cm and height 8 cm. Find the volume of water required to fill the vessel.
If this cone is replaced by another cone, whose height is 134cm and the radius of whose base is 2 cm, find the drop in the water level.
View Solution
