An open rectangular tank 1.5 m wide 2m deep ad 2 m long is half filled with water. It is accelerated horizontally at 3.27m/s2 in the direction of its length determine the depth of water at each end of tank.
To solve the problem of determining the depth of water at each end of the tank when it is accelerated horizontally, we can follow these steps:
1. Understand the Tank Dimensions and Initial Conditions:
- The tank is 1.5 m wide, 2 m deep, and 2 m long (corrected to 3 m long).
- It is half-filled with water, which means the initial depth of water is h0=1m.
2. Identify the Acceleration:
- The tank is accelerated horizontally at a=3.27m/s2.
3. Determine the Angle of the Water Surface:
- When the tank is accelerated, the water surface will tilt, forming an angle θ with the horizontal.
- The relationship between the angle θ, the acceleration a, and gravitational acceleration g is given by:
tanθ=ag
- Here, g (acceleration due to gravity) is approximately 9.8m/s2.
- Substituting the values:
tanθ=3.279.8≈0.333
- To find θ, we can use the arctangent function, but for our purpose, we will use tanθ directly in calculations.
4. Calculate the Depth at Point A (Left End):
- The depth at point A will be reduced due to the tilt of the water surface. The distance from the center of the tank to point A is half the width of the tank:
Distance from center to A=1.52=0.75m
- The depth at point A can be calculated as:
hA=h0−(Distance×tanθ)
- Substituting the values:
hA=1−(0.75×0.333)≈1−0.25=0.75m
5. Calculate the Depth at Point B (Right End):
- The depth at point B will increase due to the tilt of the water surface. The distance from the center of the tank to point B is also 0.75m.
- The depth at point B can be calculated as:
hB=h0+(Distance×tanθ)
- Substituting the values:
hB=1+(0.75×0.333)≈1+0.25=1.25m
Final Results:
- Depth at Point A (left end): hA≈0.75m
- Depth at Point B (right end): hB≈1.25m
- The tank is 1.5 m wide, 2 m deep, and 2 m long (corrected to 3 m long).
- It is half-filled with water, which means the initial depth of water is h0=1m.
- The tank is accelerated horizontally at a=3.27m/s2.
- When the tank is accelerated, the water surface will tilt, forming an angle θ with the horizontal.
- The relationship between the angle θ, the acceleration a, and gravitational acceleration g is given by:
tanθ=ag
- Here, g (acceleration due to gravity) is approximately 9.8m/s2.
- Substituting the values:
tanθ=3.279.8≈0.333
- To find θ, we can use the arctangent function, but for our purpose, we will use tanθ directly in calculations.
- The depth at point A will be reduced due to the tilt of the water surface. The distance from the center of the tank to point A is half the width of the tank:
Distance from center to A=1.52=0.75m
- The depth at point A can be calculated as:
hA=h0−(Distance×tanθ)
- Substituting the values:
hA=1−(0.75×0.333)≈1−0.25=0.75m
- The depth at point B will increase due to the tilt of the water surface. The distance from the center of the tank to point B is also 0.75m.
- The depth at point B can be calculated as:
hB=h0+(Distance×tanθ)
- Substituting the values:
hB=1+(0.75×0.333)≈1+0.25=1.25m
- Depth at Point A (left end): hA≈0.75m
- Depth at Point B (right end): hB≈1.25m
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 1 (Elasticity)
Explore 16 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBook:ALLENChapter:ELASTICITY, SURFACE TENSION AND FLUID MECHANICSExercise:Exercise 1 (Surface Tension)
Explore 21 Videos
- CENTRE OF MASSBook:ALLENChapter:CENTRE OF MASSExercise:EXERCISE-V B
Explore 19 Videos
- ERROR AND MEASUREMENTBook:ALLENChapter:ERROR AND MEASUREMENTExercise:Part-2(Exercise-2)(B)
Explore 22 Videos
Similar Questions
A beaker filled with water, is accelerated at a rate a ms2 in forward direction. The surface of water shall make an angle
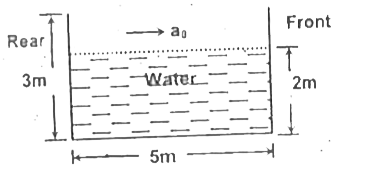
View SolutionAn open rectangular tank 5m×4m×3m high containing water upto a height of 2m is accelerated horizontally along the longer side .
(a) Determine the maximum acceleration that can be given without spilling the water .
View SolutionAn open cubical tank was initially fully filled with water. When the tank was accelerated on a horizontal plane along one of its side it was found that one thrid of volume of water was spilled out. The acceleration was
View Solution_E01_226_Q01.png)
An open retangular tank 5m×4m×3m high containing water upto a height of 2m is accelerated horizontally along the longer side.
(i). Determine the maximum acceleration that can be given without spilling the water.
(ii). Calculate the percentage of water split over if this acceleration of increased by 20%
(iii). If initially the tank is closed at the top and its accelerated horizontally by 9m/s2 find the gauge pressure at the bottom of the front and rear walls of the tank.
View SolutionA rectangular park is 2034 m long and 1512 m wide. What is the area of the park?
View SolutionA closed rectangular tank 10m long, 5m wide and 3m deep is completely filled with an oil of specific gravity 0.92. Find the pressure difference between the rear and front corners of the tank, if it is moving with an acceleration of 3m/s2 in the horizontal direction.
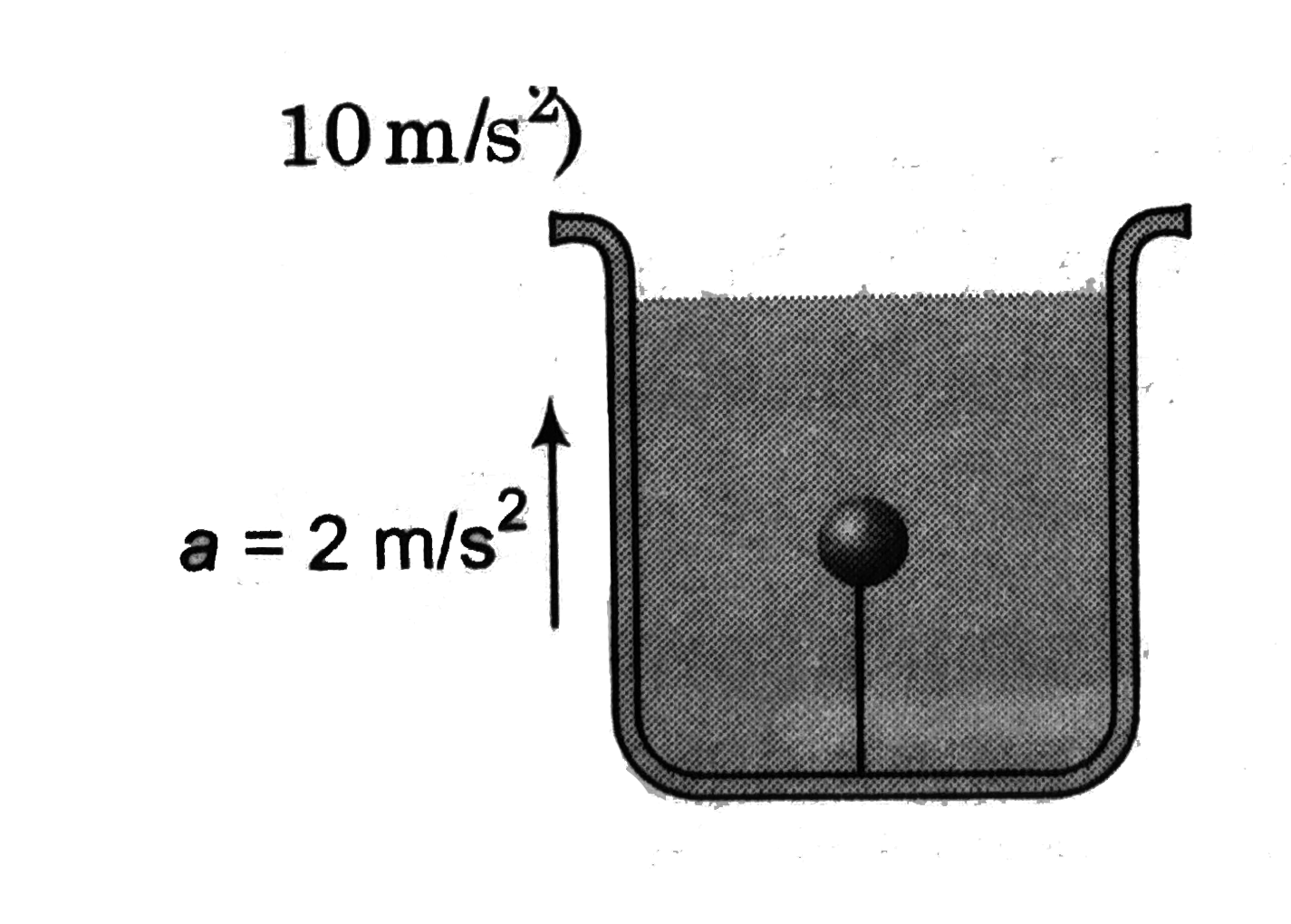
View SolutionA solid sphere of mass m=2kg and density ρ=500kg/m3 is held stationary relative to a tank filled with water. The tank is acceerating upward with acceleration 2m/s2. Calculate
(a) Tension in the thread connected between the sphere and the bottom of the tank.
(b) If the thread snaps, calculate the acceleration of sphere with respect to the tank. (Density of water=1000kg/m3,g=10m/s2)
View SolutionA spherical tank of 1.2m radius is half filled with oil of relative density 0.8. If the tank is given a horizontal acceleration of 10m/s2, the maximum pressure on the tank is √2P pascal. Find the value of P.
View SolutionA rectangular diesel tanker is 2m long, 2m wide and 40cm deep. How many litres of diesel can it hold?
View SolutionA tank 5 m high is half filled with water and then is filled to top with oil of density 0.85g/cm3 The pressure at the bottom of the tank, due to these liquids is
View Solution

